Exam 7: Vector Spaces
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
If S spans a subspace of a vector space V, then S is linearly independent in V.
Free
(True/False)
4.9/5  (37)
(37)
Correct Answer:
False
For every 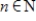 , the set
, the set 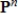 of all polynomials of degree less than or equal to n is a subspace of
of all polynomials of degree less than or equal to n is a subspace of 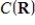 .
.
Free
(True/False)
4.9/5  (35)
(35)
Correct Answer:
True
If S spans a vector space V, but S is not linearly independent in V, then there exists a vector v in S such that the set difference 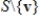 also spans V.
also spans V.
Free
(True/False)
4.8/5  (36)
(36)
Correct Answer:
True
Determine the dimension of the subspace S of 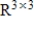 consisting of all matrices whose trace is 0.
consisting of all matrices whose trace is 0.
(Essay)
4.7/5  (37)
(37)
The set V of all nonnegative real numbers, using the usual rules for vector addition and scalar multiplication in R, is a vector space.
(True/False)
4.9/5  (36)
(36)
Determine the dimension of the subspace S of 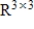 consisting of all matrices A such that
consisting of all matrices A such that
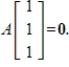
(Essay)
4.9/5  (37)
(37)
Let V be the set of all vectors 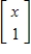 , where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.
, where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.
(Short Answer)
4.9/5  (31)
(31)
In the vector space 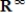 , let S be the set of all sequences
, let S be the set of all sequences 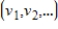 such that
such that 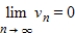 . Determine if S is a subspace of
. Determine if S is a subspace of 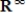 , and if not explain why.
, and if not explain why.
(Short Answer)
4.9/5  (45)
(45)
In the vector space 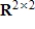 , let S be the set of matrices A such that
, let S be the set of matrices A such that 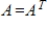 . Determine if S is a subspace of
. Determine if S is a subspace of 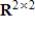 , and if not explain why.
, and if not explain why.
(Short Answer)
4.7/5  (30)
(30)
If V is a vector space and 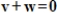 for all vectors v and w in V, then V consists of only the zero vector.
for all vectors v and w in V, then V consists of only the zero vector.
(True/False)
4.9/5  (40)
(40)
Let V be the set of all functions f : R 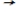 R such that
R such that 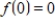 . Using the usual rules for vector addition and scalar multiplication of functions, determine if V is a vector space, and if not explain why.
. Using the usual rules for vector addition and scalar multiplication of functions, determine if V is a vector space, and if not explain why.
(Short Answer)
4.9/5  (31)
(31)
Let V be a vector space with vector addition 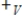 and scalar multiplication
and scalar multiplication 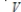 , and let W be a vector space with vector addition
, and let W be a vector space with vector addition 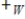 and scalar multiplication
and scalar multiplication 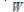 . Define
. Define 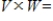
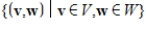 , with addition
, with addition 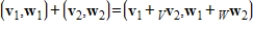 and scalar multiplication
and scalar multiplication 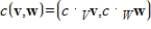 . Determine if
. Determine if 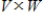 is a vector space, and if not explain why.
is a vector space, and if not explain why.
(Essay)
4.7/5  (33)
(33)
If every finite set S in a vector space V fails to span V, then 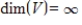 .
.
(True/False)
4.7/5  (31)
(31)
In the vector space 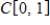 , let S be the set of all functions f such that
, let S be the set of all functions f such that 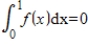 . Determine if S is a subspace, and if not explain why.
. Determine if S is a subspace, and if not explain why.
(Short Answer)
4.8/5  (24)
(24)
If 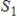 and
and 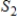 are infinite-dimensional subspaces of a vector space V, then
are infinite-dimensional subspaces of a vector space V, then 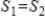 .
.
(True/False)
4.7/5  (36)
(36)
Showing 1 - 20 of 45
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)