Deck 15: Random- and Mixed-Effects Analysis of Variance Models
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/7
Play
Full screen (f)
Deck 15: Random- and Mixed-Effects Analysis of Variance Models
1
Complete the following ANOVA summary table for a two-factor model, where there are two levels of factor A (fixed program effect) and five levels of factor B (random school effect). Each cell of the design includes seven students ( = .05).
There are 2 levels of the fixed factor A, so J = 2.
There are 5 levels of the random factor B, so K = 5.
Each cell has 7 students, so n = 7. N = 2*5*7 = 70.
dfA = J- 1 = 2 - 1 = 1, dfB = K - 1 = 5 - 1 = 4, dfAB = (J -1)(K- 1) = 1*4 = 4, dfwith = N - JK = 70 - 2*5 = 60, dftotal = N - 1 = 70 - 1 = 69.
SSAB = MSAB*dfAB = 20*4 = 80;
SSwith = SStotal - SSA - SSB - SSAB = 690 100 210 80 = 300.
MSA = SSA/dfA = 100/1 = 100; MSB = SSB/dfB = 210/4 = 52.5;
MSwith = SSwith/dfwith = 300/60 = 5.
FA = MSA/MSAB = 100/20 = 5; critical value for A = .05F1,4 = 7.71 > FA, fail to reject H0.
FB = MSB/MSwith = 52.5/5 = 10.5; critical value for B = .05F4,60 = 2.53 < FB, reject H0.
FAB = MSAB/MSwith = 20/5 = 4; critical value for AB = .05F4,60 = 2.53 < FAB, reject H0.
There are 5 levels of the random factor B, so K = 5.
Each cell has 7 students, so n = 7. N = 2*5*7 = 70.
dfA = J- 1 = 2 - 1 = 1, dfB = K - 1 = 5 - 1 = 4, dfAB = (J -1)(K- 1) = 1*4 = 4, dfwith = N - JK = 70 - 2*5 = 60, dftotal = N - 1 = 70 - 1 = 69.
SSAB = MSAB*dfAB = 20*4 = 80;
SSwith = SStotal - SSA - SSB - SSAB = 690 100 210 80 = 300.
MSA = SSA/dfA = 100/1 = 100; MSB = SSB/dfB = 210/4 = 52.5;
MSwith = SSwith/dfwith = 300/60 = 5.
FA = MSA/MSAB = 100/20 = 5; critical value for A = .05F1,4 = 7.71 > FA, fail to reject H0.
FB = MSB/MSwith = 52.5/5 = 10.5; critical value for B = .05F4,60 = 2.53 < FB, reject H0.
FAB = MSAB/MSwith = 20/5 = 4; critical value for AB = .05F4,60 = 2.53 < FAB, reject H0.
2
Complete the following ANOVA summary table for a two-factor model, where there are three levels of factor A (random dosage effect) and four levels of factor B (random physician effect). Each cell of the design includes six patients ( = .05).
There are 3 levels of the fixed factor A, so J = 3.
There are 4 levels of the random factor B, so K = 4.
Each cell has 6 students, so n = 6. N = 3*4*6 = 72.
dfA = J- 1 = 3 - 1 = 2, dfB = K - 1 = 4 - 1 = 3, dfAB = (J - 1)(K - 1) = 2*3 = 6, dfwith = N - JK = 72 - 3*4 = 60, dftotal = N - 1 = 72 - 1 = 71.
SSB = MSB*dfB = 15*3 = 45; SSwith = MSwith*dfwith = 1*60 = 60;
SSAB = SStotal - SSA - SSB - SSwith = 160 - 25 - 45 - 60 = 30.
MSA = SSA/dfA = 25/2 = 12.5; MSAB = SSAB/dfAB = 30/6 = 5.
FA = MSA/MSAB = 12.5/5 = 2.5; critical value for A = .01F2,6 = 10.93 > FA, fail to reject H0.
FB = MSB/MSAB = 15/5 = 3; critical value for B = .01F3,6 = 9.78 < FB, fail to reject H0.
FAB = MSAB/MSwith = 5/1 = 5; critical value for AB= .01F6,60 = 3.12 < FAB, reject H0.
There are 4 levels of the random factor B, so K = 4.
Each cell has 6 students, so n = 6. N = 3*4*6 = 72.
dfA = J- 1 = 3 - 1 = 2, dfB = K - 1 = 4 - 1 = 3, dfAB = (J - 1)(K - 1) = 2*3 = 6, dfwith = N - JK = 72 - 3*4 = 60, dftotal = N - 1 = 72 - 1 = 71.
SSB = MSB*dfB = 15*3 = 45; SSwith = MSwith*dfwith = 1*60 = 60;
SSAB = SStotal - SSA - SSB - SSwith = 160 - 25 - 45 - 60 = 30.
MSA = SSA/dfA = 25/2 = 12.5; MSAB = SSAB/dfAB = 30/6 = 5.
FA = MSA/MSAB = 12.5/5 = 2.5; critical value for A = .01F2,6 = 10.93 > FA, fail to reject H0.
FB = MSB/MSAB = 15/5 = 3; critical value for B = .01F3,6 = 9.78 < FB, fail to reject H0.
FAB = MSAB/MSwith = 5/1 = 5; critical value for AB= .01F6,60 = 3.12 < FAB, reject H0.
3
To examine development in the pedagogical content knowledge (PCK) of new teachers, 12 novice teachers are measured on their PCK at the beginning of their teaching career, at the end of the first semester, and at the end of the first school year. The scale that measures PCK ranges from 0 to 45, with higher scores reflecting greater levels of PCK. The data are shown below. Conduct a one-factor repeated measures ANOVA to determine the mean differences across time, using = .05. Use the Bonferroni method to detect exactly where the differences are among the time points (if they are different).
Procedure:
Create a data set with three variables: Time 1, Time 2, and Time 3. The data set should have 12 cases, representing 12 teachers.
1. Go to Analyze General Linear Model Repeated Measures.
"2. For Within-Subject Factor Name, enter ""Time.""
For Number of Levels, enter 3 (i.e., 3 time points). Click Add.
For Measure Name, enter ""PCK."" Click Add."
3. Click Define. Move Time1 through Time3 in the left box to Within-Subjects Variables (Time).
4. Click Options. Move "Time" to Display Means for. Select Compare main effects. Select Bonferroni under Confidence interval adjustment. Select Descriptive statistics, Estimates of effect size, and Observed power. Click Continue.
5. To get profile plots, click Plots. Move "Time" to the box under Horizontal Axis. Click Add. Click Continue.
"6. Click OK.
Selected SPSS Output:
Pairwise Comparisons: Bonferroni Method
Measure: PCK
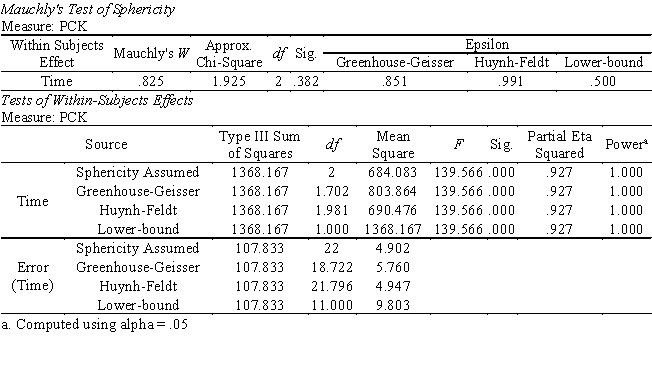
The results of the test of sphericity give no evidence against the assumption of sphericity (Mauchly's W = .825, 2 = 1.925, df = 2, p = .382).
Based on the results of the one-factor repeated measures ANOVA, the effect of the within-subjects factor, Time, is significant at the .05 level (F2,22 = 139.556, p < .001) with large effect size (partial 2 = .927) and maximum observed power, implying that the novice teachers' average level of PCK has changed significantly across three time points.
Results of MCP, using the Bonferroni method, reveal significant differences among all pairs of time points. Specifically, the level of PCK increased significantly from Time 1 (i.e., the beginning of the school year) to Time 2 (i.e., the end of the first semester), from Time 2 to Time 3 (i.e., the end of the school year), and from Time 1 to Time 3. The results therefore suggest that the novice teachers' pedagogical content knowledge increases substantially in their first two semesters of teaching."
Create a data set with three variables: Time 1, Time 2, and Time 3. The data set should have 12 cases, representing 12 teachers.
1. Go to Analyze General Linear Model Repeated Measures.
"2. For Within-Subject Factor Name, enter ""Time.""
For Number of Levels, enter 3 (i.e., 3 time points). Click Add.
For Measure Name, enter ""PCK."" Click Add."
3. Click Define. Move Time1 through Time3 in the left box to Within-Subjects Variables (Time).
4. Click Options. Move "Time" to Display Means for. Select Compare main effects. Select Bonferroni under Confidence interval adjustment. Select Descriptive statistics, Estimates of effect size, and Observed power. Click Continue.
5. To get profile plots, click Plots. Move "Time" to the box under Horizontal Axis. Click Add. Click Continue.
"6. Click OK.
Selected SPSS Output:

Pairwise Comparisons: Bonferroni Method
Measure: PCK
The results of the test of sphericity give no evidence against the assumption of sphericity (Mauchly's W = .825, 2 = 1.925, df = 2, p = .382).
Based on the results of the one-factor repeated measures ANOVA, the effect of the within-subjects factor, Time, is significant at the .05 level (F2,22 = 139.556, p < .001) with large effect size (partial 2 = .927) and maximum observed power, implying that the novice teachers' average level of PCK has changed significantly across three time points.
Results of MCP, using the Bonferroni method, reveal significant differences among all pairs of time points. Specifically, the level of PCK increased significantly from Time 1 (i.e., the beginning of the school year) to Time 2 (i.e., the end of the first semester), from Time 2 to Time 3 (i.e., the end of the school year), and from Time 1 to Time 3. The results therefore suggest that the novice teachers' pedagogical content knowledge increases substantially in their first two semesters of teaching."
4
Dr. Bellus wants to study how people's perception of attractiveness is affected by the gender of the subjects, and the facial expression of the object. Each participant views six headshots (in random order) of the same person, who demonstrates different facial expressions (joy, surprise, fear, anger, sadness, and disgust) in each picture. The participants are then asked to rate the attractiveness level of each picture. The rating is the dependent variable. Below is the selected output of a two-factor split plot ANOVA.
Test of Between-Subjects Effects
Test of Within-Subjects Effects
a. Identify the between-subjects factor and within-subjects factor.
b. Are the effects significant ( = .05)? What do these results tell us about people's perception of attractiveness?
c. Is MCP necessary? If so, on which effect(s) should we conduct MCP?
Test of Between-Subjects Effects
Test of Within-Subjects Effects
a. Identify the between-subjects factor and within-subjects factor.
b. Are the effects significant ( = .05)? What do these results tell us about people's perception of attractiveness?
c. Is MCP necessary? If so, on which effect(s) should we conduct MCP?

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
5
A researcher interested in making generalizations about the entire population of categories of the independent variable, not just the levels that were sampled, should pursue what type of ANOVA model?
A) Covariate model
B) Fixed effect
C) Random effect
D) Repeated measure
A) Covariate model
B) Fixed effect
C) Random effect
D) Repeated measure

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following is not a characteristic of a two-factor random effects ANOVA?
A) Two factors (or independent variables) each with two or more levels
B) The levels for one of the factors are randomly sampled from the population of levels (i.e., the random-effects factor) and all of the levels of interest for the second factor are included in the design (i.e., the fixed-effects factor)
C) Subjects are randomly selected and assigned to one category of one independent variable only
D) The dependent variable is measured at least at the interval level
A) Two factors (or independent variables) each with two or more levels
B) The levels for one of the factors are randomly sampled from the population of levels (i.e., the random-effects factor) and all of the levels of interest for the second factor are included in the design (i.e., the fixed-effects factor)
C) Subjects are randomly selected and assigned to one category of one independent variable only
D) The dependent variable is measured at least at the interval level

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following are variations of a two-factor mixed-effects ANOVA?
A) One where factor A is fixed and factor B is fixed, and the other where factor A is random and factor B is random.
B) One where factor A is fixed and factor B is random, and the other where factor A is fixed and factor B is fixed.
C) One where factor A is fixed and factor B is random, and the other where factor A is random and factor B is fixed.
D) One where factor A is random and factor B is random, and the other where factor A is fixed and factor B is fixed.
A) One where factor A is fixed and factor B is fixed, and the other where factor A is random and factor B is random.
B) One where factor A is fixed and factor B is random, and the other where factor A is fixed and factor B is fixed.
C) One where factor A is fixed and factor B is random, and the other where factor A is random and factor B is fixed.
D) One where factor A is random and factor B is random, and the other where factor A is fixed and factor B is fixed.

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck


