Deck 4: Equivalence for Repeated Cash Flows
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/22
Play
Full screen (f)
Deck 4: Equivalence for Repeated Cash Flows
1
A set of cash flows are given in table below, using the principles of equivalence, determine the value "Y" for an interest rate of 8% compounded annually.
A) $1,402.34
B) $1,887.50
C) $1,107.78
D) $2,328.25
A) $1,402.34
B) $1,887.50
C) $1,107.78
D) $2,328.25
$1,887.50
2
For an interest rate of 10% compounded annually, evaluate the value of "X" from the cash flows given in table below.
A) $2,316.85
B) $3,295.43
C) $1,064.74
D) $1,102.75
A) $2,316.85
B) $3,295.43
C) $1,064.74
D) $1,102.75
$2,316.85
3
For the cash flow diagram below, determine the value of P
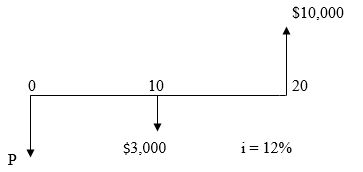
A) $119.26
B) $195.49
C) $71
D) $147.20
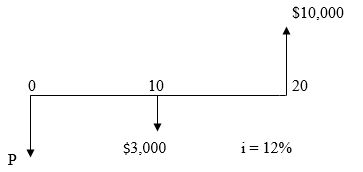
A) $119.26
B) $195.49
C) $71
D) $147.20
$71
4
Four different choices are given to determine the unknown value of "X" from the cash flow diagram given below. Use an interest rate of i =6%.
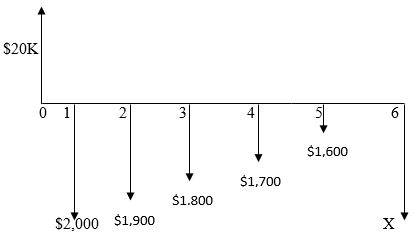
A) X= {20,000 - 2,000(P/A, 6%, 6) +100(P/G, 6%, 6)} (P/F, 6%, 6)
B) X= {20,000 - 2,000(P/A, 6%, 5) +100(P/G, 6%, 5)} (F/P, 6%, 6)
C) X= {20,000 - 2,000(P/A, 6%, 6) +100(P/G, 6%, 6)} (F/P, 6%, 6)
D) X= {20,000 - 2,000(P/A, 6%, 6) +100(P/G, 6%, 5)} (P/F, 4%, 6)

A) X= {20,000 - 2,000(P/A, 6%, 6) +100(P/G, 6%, 6)} (P/F, 6%, 6)
B) X= {20,000 - 2,000(P/A, 6%, 5) +100(P/G, 6%, 5)} (F/P, 6%, 6)
C) X= {20,000 - 2,000(P/A, 6%, 6) +100(P/G, 6%, 6)} (F/P, 6%, 6)
D) X= {20,000 - 2,000(P/A, 6%, 6) +100(P/G, 6%, 5)} (P/F, 4%, 6)

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
5
What is the present worth of the cash flows in table below? Use an interest rate of 6% compounded annually.
A) $89,263
B) $85,496
C) $89,915.77
D) $91,611
A) $89,263
B) $85,496
C) $89,915.77
D) $91,611

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
6
Given the cash flow diagram below, evaluate the value of "A" for an interest rate of 7%.
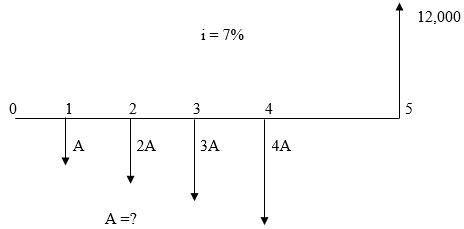
A) $585
B) $1045.72
C) $1200
D) $915

A) $585
B) $1045.72
C) $1200
D) $915

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
7
Mary is planning to repay a debt of 50,000 with a quarterly payment $2,400 for the next 23 quarters and a final payment of "X" dollars at the end of 24-th quarter. If the interest rate is 12% per year, compounded quarterly, how much will be Mary's final payment?
A) $21,426
B) $22,176
C) $23,010
D) $23,920
A) $21,426
B) $22,176
C) $23,010
D) $23,920

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
8
Determine the value of P from the cash flows shown in table below. Interest rate = 10%.
A) $8,102
B) $5,197.5
C) $9,211.2
D) $7,284.9
A) $8,102
B) $5,197.5
C) $9,211.2
D) $7,284.9

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
9
Tom started investing, as soon as he started his first job, at the rate of $400 per month as soon as get paid into a savings account that earns an interest of 1% per month. Which of the following expression may be used to determine the account value 10 years from now?
A) F = [4,800(P/A, 12%, 10)] [(F/P, 12%, 10)]
B) F = 400[(P/A, 1%, 120) (F/P, 12%, 5)]
C) F= [400/0.01] (F/P, 1%, 60)
D) F= 400(F/A, 1%, 120)
A) F = [4,800(P/A, 12%, 10)] [(F/P, 12%, 10)]
B) F = 400[(P/A, 1%, 120) (F/P, 12%, 5)]
C) F= [400/0.01] (F/P, 1%, 60)
D) F= 400(F/A, 1%, 120)

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
10
Choose the equation below that can be used to determine the value of "P" for a known interest rate, i.
A) P = 10,000(P/F, i%, 5) - 2,000(P/G, i%, 5)
B) P = 10,000- 1,000(P/G, i%, 5) (F/P, i%, 5)
C) P= 10,000(P/F, i%, 5) -2,000(P/G, i%, 5)
D) P= -10,000(P/F, i%, 5) + 2,000(P/G, i%, 4)
A) P = 10,000(P/F, i%, 5) - 2,000(P/G, i%, 5)
B) P = 10,000- 1,000(P/G, i%, 5) (F/P, i%, 5)
C) P= 10,000(P/F, i%, 5) -2,000(P/G, i%, 5)
D) P= -10,000(P/F, i%, 5) + 2,000(P/G, i%, 4)

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
11
Ben invested $20,000 into a money market account and took out $5,000 at the end of year 5. He found out at the end of 10 years that he had as of $50,000 in the account.
What is the annual interest rate Ben had earned on this investment?
A) 8%
B) 12.93%
C) 15.23%
D) 11.38%
What is the annual interest rate Ben had earned on this investment?
A) 8%
B) 12.93%
C) 15.23%
D) 11.38%

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
12
Given the cash flow diagram below, evaluate the "X" value using an interest rate of 8%.
A) $7,201
B) $6,781
C) $3410.23
D) $6,525
A) $7,201
B) $6,781
C) $3410.23
D) $6,525

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
13
IAN Tech is saving $10,000 a month in a money fund to pay for equipment that will cost $700,000 five years from now. If the interest rate is 1/4% per month, how much additional funds will be needed to pay for this equipment?
A) $48,239
B) $53,530
C) $59,750
D) $25,070
A) $48,239
B) $53,530
C) $59,750
D) $25,070

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
14
Determine the unknown from the cash flow diagram shown below. i = 10%.
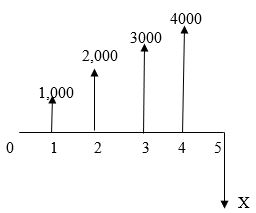
A) $12,160
B) $14,500
C) $10,108
D) $12,809

A) $12,160
B) $14,500
C) $10,108
D) $12,809

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
15
Given a series of cash flows in the table below, determine the value of "y". i=6%
A) $21,025
B) $21,960
C) $23,821
D) $22,507
A) $21,025
B) $21,960
C) $23,821
D) $22,507

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
16
Given the cash flow table below, determine the unknown value "X" for an interest rate of 6%.
A) $2436.89
B) $3129.41
C) $2935.66
D) $1610.53
A) $2436.89
B) $3129.41
C) $2935.66
D) $1610.53

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
17
Case Study 4
Daniel borrowed $20,000 with a promise to repay the loan in 6 years with a uniform monthly payment and a single payment of $2,000 at the end of six years at a nominal interest rate of 12% per year.
-A. What is the amount of each payment?
B. What is the amount of interest paid in the first payment?
C. What will be the loan balance immediately after the 48th payment?
Daniel borrowed $20,000 with a promise to repay the loan in 6 years with a uniform monthly payment and a single payment of $2,000 at the end of six years at a nominal interest rate of 12% per year.
-A. What is the amount of each payment?
B. What is the amount of interest paid in the first payment?
C. What will be the loan balance immediately after the 48th payment?

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
18
In order to use the gradient series factors to solve a set of given cash flows, the cash flows must increase or decrease gradually by the same amount every year, starting year 2 and must have zero cash flow in year 1.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
19
In developing cash flow diagrams the convention is to use a negative cash flow for receipts.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
20
The weekly payment for a $500 loan to be paid back in 104 payments at an interest rate of 0.25% per week is $6.82.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
21
Interest compounding daily than continuous compounding for a known interest rate will provide a larger yield.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
22
If the uniform series capital recovery factor is 0.1359 and the sinking fund factor is 0.0759, then the interest rate is 6%.

Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck


