Deck 9: Bivariate Correlation and Regression

Question 1

To learn about the accuracy of a relationship between two variables (continuous), as well as its strength and direction, the most appropriate statistical test to run is

A) ANOVA.
B) Regression.
C) Chi square.
D) Correlation.

Answer 1

Correlation.

Question 2

To predict a certain outcome having detailed knowledge about the independent variable, which is impacting the dependent variable, the most appropriate statistical test to run is

A) ANOVA.
B) Regression.
C) Chi square.
D) Correlation.

Answer 2

Regression.

Question 3

Many formulas utilized in statistics are complex. However, one basic formula used in regression is a classic algebraic equation: y = a + bx. Explain the variables within this formula.

Answer 3

y = any given value on the y-axis that we want to predict by knowing the distribution of the independent variable (x).
a = the constant (or y-intercept) and tells us where the regression line touches the y-axis. In other words, the constant tells us the value of the independent variable (y) if x equals zero.
b = the slope, which is defined as the vertical divided by the horizontal distance between any two points on the line.
x = a given value on the x-axis.

Question 4

Assume you have computed b = 6. Interpret your result in words.

Question 5

To warm up, let us start with a problem that has a "perfect" regression line. Assume that the state prison wants to encourage prisoners to get involved in education. Thus, the prison administration offers that for every hour spent on education, inmates receive 5 additional minutes in the prison yard.
a. Compute beta and interpret your finding.
b. Compute the constant (y intercept or a) and interpret your finding.

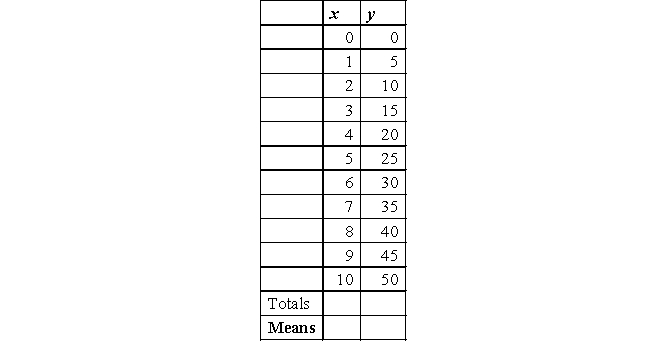
c. Assume that John (inmate) has studied 17 hours in the previous week; how many minutes of additional yard time did he earn? Use the classic algebraic equation (y = a + bx) to calculate the amount of minutes earned and interpret your result.
d. Next, you want to predict the total time an inmate is allowed to spend in the yard (weekly allowance + additional time earned). The weekly allowance regarding yard time is (without additional time earned) 630 minutes (10.5 hours).

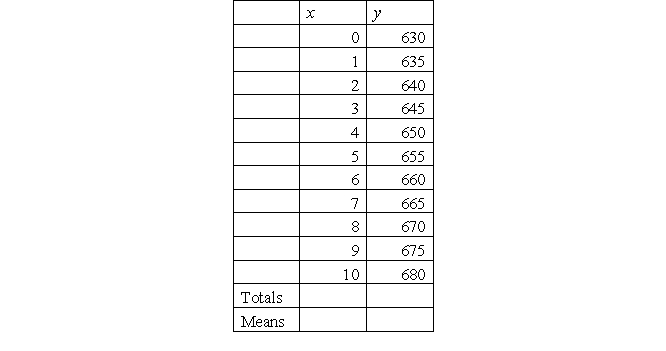
i. Compute beta.
ii. Compute the constant (a or y-intercept).
iii. How many minutes (total) is John allowed to spend in the prison yard if he has studied for 21 hours? Use the classic algebraic equation (y = a + bx).

Question 6

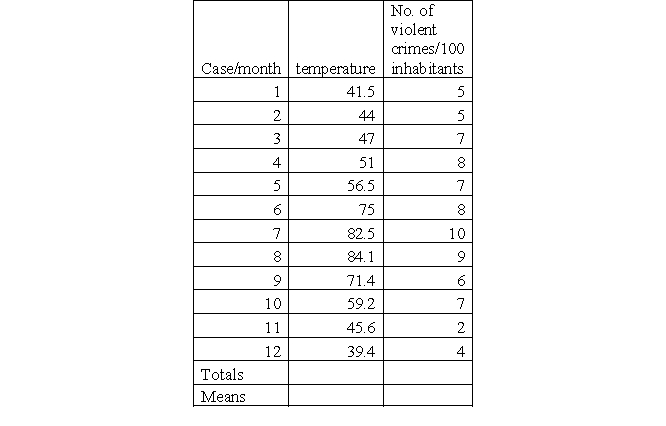
Academic literature found evidence that there is a relationship between temperature and the frequency of the occurrence of violent crimes. Utilizing data derived from the local police department (number of violent crimes/month/100 inhabitants) and meteorological data (average temperature/month), you want to determine the relationship between temperature (IV) and the frequency of violent crime (DV). Find the distribution of both variables in the table below.
a. Use a spreadsheet program to create a scatterplot or draw it by hand. Describe what you see.
b. Compute beta (b) and interpret your result.
c. Compute the constant (a) and interpret your result.
d. Assume you want to predict the frequency of violent crimes in a month with an average temperature of 90.5 degrees Fahrenheit. Compute y.

Question 7

Using the example from problem 2:
a. State your null and your alternative hypotheses.
b. Determine the strength and direction of the relationship by computing Pearson's r. Interpret your results.
c. Compute r² and interpret your result.

Question 8

You are interested in the relationship between the visual consumption of crime shows (average per day in hours) and levels of fear of crime (on a scale of 0-30). You have asked a random sample of 14 individuals (random digit dialing) how many hours they watch TV crime shows (per week) and about their level of fear of crime on a scale from 1 to 30. You select an alpha level of 0.05. Because you are uncertain about the direction of the relationship, you choose to utilize two-tailed t values.
a. State your null and alternative hypotheses.
b. Utilizing the data from the table presented below:
i. Compute beta (b). Interpret your result.
ii. Compute the constant (a) and interpret your result.
iii. Determine the strength and direction of the relationship by computing Pearson's r. Interpret your result.
iv. Compute r² and interpret your result.
v. Compute the prediction error you could possibly have knowing nothing about the distribution of the independent variable (hours of crime shows watched).
vi. Compute the unexplained variance.
vii. Compute the explained variance.
c. Make a decision rule to determine significance.
d. Make a decision and interpret your results.
e. Compute the standard error of estimate.
$$\begin{array} { | c | } \hline \text { Case } \\\hline \\\hline 1 \\\hline 2 \\\hline 3 \\\hline 4 \\\hline 5 \\\hline 6 \\\hline 7 \\\hline 8 \\\hline 9 \\\hline 10 \\\hline 11 \\\hline 12 \\\hline 13 \\\hline 14 \\\hline\end{array}$$

Question 9

It is debated whether IQ scores influence criminal behavior (either directly or indirectly). It is argued that the majority of criminals have an IQ that lies 8 points below (92) the average IQ (100). You draw a random sample of 15 individuals of age 18+, assess the IQ of participants, and ask them about their criminal history (number of offenses committed, not including minor traffic violations). You select an alpha of 0.05. The results of your assessment are to be found in the table presented below.
a. State your null and alternative hypotheses.
b. State your decision rule to determine statistical significance.
c. Utilizing the data from the table presented below:
i. Compute beta (b).
ii. Compute the constant (a).
iii. Determine the strength and direction of the relationship by computing Pearson's r.
iv. Compute r².
v. Compute the prediction error you could possibly have if you know nothing about the distribution of the independent variable (IQ score).
vi. Compute the unexplained variance.
vii. Compute the explained variance.
d. Make a decision.
e. Compute the standard error of estimate.
f. INTERPRET ALL YOUR RESULTS.
$$\begin{array} { | r | r | r | } \hline { \text { Case } } & \text { IQ } ( x ) & \begin{array} { l } \text { No. of } \\\text { offenses } \\( y )\end{array} \\\hline 1 & 90 & 4 \\\hline 2 & 110 & 1 \\\hline 3 & 89 & 4 \\\hline 4 & 95 & 3 \\\hline 5 & 92 & 5 \\\hline 6 & 91 & 4 \\\hline 7 & 102 & 0 \\\hline 8 & 99 & 2 \\\hline 9 & 76 & 3 \\\hline 10 & 99 & 1 \\\hline 11 & 92 & 6 \\\hline 12 & 98 & 1 \\\hline 13 & 111 & 1 \\\hline 14 & 100 & 2 \\\hline 15 & 93 & 6 \\\hline\end{array}$$