Deck 3: Additional Applications of the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/134
Play
Full screen (f)
Deck 3: Additional Applications of the Derivative
1
Find all intervals where the derivative of the function shown below is negative. 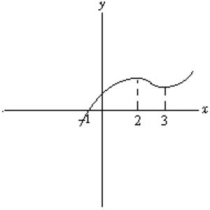

2 < x < 3
2
The derivative of function shown below is negative on the interval shown. 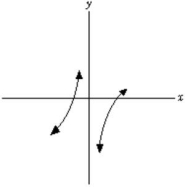

False
3
Find all intervals where the derivative of the function shown below is negative. 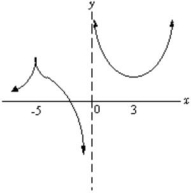

-5 < x < 0 and 0 < x < 3
4
Find the intervals of increase and decrease for the function .
A)
B)
C) Decreasing for all x
D) Increasing for all x
A)
B)
C) Decreasing for all x
D) Increasing for all x

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
5
Find the intervals of increase and decrease for the function .
A)
B)
C) Decreasing for all x
D) Increasing for all x
A)
B)
C) Decreasing for all x
D) Increasing for all x

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
6
Find the intervals of increase and decrease for .
A) Increasing on x -2 and x 3, decreasing on - 2 x 3
B) Increasing on x < -3 and x > 2, decreasing on -3 < x < 2
C) Increasing on -3 < x < 2, decreasing on x < -3 and x > 2
D) Increasing on x < -2, decreasing on x > 3
A) Increasing on x -2 and x 3, decreasing on - 2 x 3
B) Increasing on x < -3 and x > 2, decreasing on -3 < x < 2
C) Increasing on -3 < x < 2, decreasing on x < -3 and x > 2
D) Increasing on x < -2, decreasing on x > 3

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
7
Find the intervals of increase and decrease for the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
8
Find the intervals of increase and decrease for the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
9
Find the intervals of increase and decrease for . Round numbers to two decimal places, if necessary.
A) Increasing on x < 5, decreasing on x > 5
B) Increasing on x < 5 and x > 5
C) Increasing on x 0.63 and on x > 5, decreasing on 0.63 < x 5
D) Increasing on 0.63 < x 5, decreasing on x 0.63 and on x > 5
A) Increasing on x < 5, decreasing on x > 5
B) Increasing on x < 5 and x > 5
C) Increasing on x 0.63 and on x > 5, decreasing on 0.63 < x 5
D) Increasing on 0.63 < x 5, decreasing on x 0.63 and on x > 5

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
10
Find the intervals of increase and decrease for the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
11
Find the intervals of increase and decrease for the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
12
Find the intervals of increase and decrease for the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
13
Find all critical numbers of the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
14
Find all the critical numbers of the function .
A) 0, 1, -1
B) -1
C)
D) None
A) 0, 1, -1
B) -1
C)
D) None

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
15
Determine the critical points of the given function and classify each critical point as a relative maximum, a relative minimum, or neither.
A) (0, 4) relative minimum; (3, 166) neither
B) (0, 2) neither; (1, 3) relative minimum
C) (0, 2) relative minimum; (1, 4) neither
D) (0, 2) relative minimum; (1, 3) relative maximum
A) (0, 4) relative minimum; (3, 166) neither
B) (0, 2) neither; (1, 3) relative minimum
C) (0, 2) relative minimum; (1, 4) neither
D) (0, 2) relative minimum; (1, 3) relative maximum

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
16
Find all the critical numbers of the function .
A) None
B) -2, 2
C) 0, -2, 2
D)
A) None
B) -2, 2
C) 0, -2, 2
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
17
Find all the critical numbers of the function .
A) -7
B)
C) 2
D) None
A) -7
B)
C) 2
D) None

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
18
Find all the critical numbers of the function.
A) -1
B)
C)
D) None
A) -1
B)
C)
D) None

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
19
Find all the critical numbers of the function .
A) None
B) -1, 1
C) 0, -1, 1
D)
A) None
B) -1, 1
C) 0, -1, 1
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
20
Find all critical numbers of the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
21
Find all critical numbers of the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
22
Determine the critical numbers of the given function and classify each critical point as a relative maximum, a relative minimum, or neither. Round numbers to two decimal places, if necessary.
A) x = 1, 4, 7; (4, -0.22) relative maximum
B) x = 1, 4, 7; (1, 2) relative maximum; (4, -0.22) relative minimum; (7, 2) relative maximum
C) x = 1, 7; (1, 2) relative maximum; (7, 2) relative maximum
D) x = 1, 7; (1, 2) relative maximum; (7, 2) relative minimum
A) x = 1, 4, 7; (4, -0.22) relative maximum
B) x = 1, 4, 7; (1, 2) relative maximum; (4, -0.22) relative minimum; (7, 2) relative maximum
C) x = 1, 7; (1, 2) relative maximum; (7, 2) relative maximum
D) x = 1, 7; (1, 2) relative maximum; (7, 2) relative minimum

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
23
Find all critical numbers of the function .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
24
The revenue derived from the production of x units of a particular commodity is million dollars. What level of production results in maximum revenue? What is the maximum revenue? Round numbers to two decimal places, if necessary.
A) Maximum at x = 6 and maximum revenue is R(6) = 18 (million dollars)
B) Maximum at x = 6 and maximum revenue is R(6) = 2.05 (thousand dollars)
C) Maximum at x = 6 and maximum revenue is R(6) = 3 (million dollars)
D) Maximum at x = 7 and maximum revenue is R(7) = 2.05 (million dollars)
A) Maximum at x = 6 and maximum revenue is R(6) = 18 (million dollars)
B) Maximum at x = 6 and maximum revenue is R(6) = 2.05 (thousand dollars)
C) Maximum at x = 6 and maximum revenue is R(6) = 3 (million dollars)
D) Maximum at x = 7 and maximum revenue is R(7) = 2.05 (million dollars)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
25
Find constants a, b, and c so that the graph of the function has a relative maximum at (5, 25) and crosses the y-axis at (0, 5).
A) , b = -8, c = -5
B) , b = 8, c = 5
C) , b = 8, c = 5
D) , b = -8, c = 5
A) , b = -8, c = -5
B) , b = 8, c = 5
C) , b = 8, c = 5
D) , b = -8, c = 5

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
26
The function graphed below has a positive second derivative everywhere. 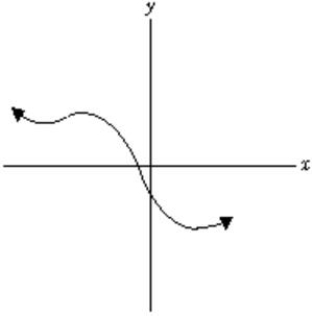


Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
27
Determine where the second derivative in the function graphed below is positive. 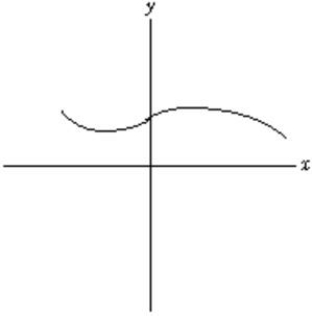


Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
28
The function graphed below has a negative second derivative everywhere. 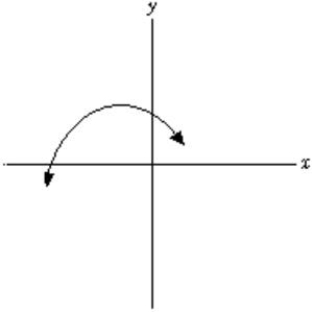


Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
29
Determine where the second derivative in the function graphed below is positive. 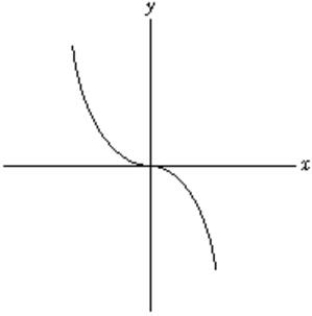


Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
30
Determine where the graph of is concave up and concave down.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
31
Determine where the graph of is concave up and concave down.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
32
Determine where the graph of is concave down.
A) x > 1
B) x < 1
C) x > -1
D) x < -1
A) x > 1
B) x < 1
C) x > -1
D) x < -1

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
33
Determine where the graph of is concave down.
A) For x < 3
B) For x > 3
C) For x < -3
D) For x > -3
A) For x < 3
B) For x > 3
C) For x < -3
D) For x > -3

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
34
Determine where the graph of is concave up and concave down.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
35
The graph of is concave down for .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
36
The inflection point of is (-2, 3).

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
37
Determine where the graph of is concave up.
A) for x < -1 and x > 1
B) for -1 < x < 1
C) Everywhere
D) Nowhere
A) for x < -1 and x > 1
B) for -1 < x < 1
C) Everywhere
D) Nowhere

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
38
Locate all inflection points of .
A) (1, 9) and (-4, -486)
B) (1, 9)
C) None
D) (0, 26)
A) (1, 9) and (-4, -486)
B) (1, 9)
C) None
D) (0, 26)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
39
Determine where the graph of is concave up.
A) For x < -1 and x > 1
B) For -1 < x < 1
C) Everywhere
D) Nowhere
A) For x < -1 and x > 1
B) For -1 < x < 1
C) Everywhere
D) Nowhere

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
40
The graph of is concave up for .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
41
The graph of is concave up everywhere.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
42
Determine where the graph of is concave up and concave down.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
43
Locate all inflection points of .
A)
B)
C) (0, 0)
D)
A)
B)
C) (0, 0)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
44
The function has a relative maximum at x = 1.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
45
The function has a relative minimum at x = 1.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
46
Let . Find all critical points of f and use the second derivative test to classify each as a relative maximum, a relative minimum, or neither.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
47
The second derivative test reveals that has
A) a relative maximum at
B) a point of inflection at
C) a relative minimum at x = 0.
D) a point of inflection at x = 3.
A) a relative maximum at
B) a point of inflection at
C) a relative minimum at x = 0.
D) a point of inflection at x = 3.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
48
Use the second derivative test to find the relative maxima and minima of the function .
A) Relative maximum at (1, 109); relative minimum at (-3, -19)
B) Relative maximum at (-3, -19); relative minimum at (-1, 45)
C) Relative maximum at (-3, -18); relative minimum at (1, 109)
D) Relative maximum at (-3, 109); relative minimum at (1, -19)
A) Relative maximum at (1, 109); relative minimum at (-3, -19)
B) Relative maximum at (-3, -19); relative minimum at (-1, 45)
C) Relative maximum at (-3, -18); relative minimum at (1, 109)
D) Relative maximum at (-3, 109); relative minimum at (1, -19)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
49
The second derivative test reveals that f (x) =x2- 5 has
A) a relative maximum at
B) a point of inflection at
C) a relative minimum at x = 0.
D) nothing significant at x = 5.
A) a relative maximum at
B) a point of inflection at
C) a relative minimum at x = 0.
D) nothing significant at x = 5.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
50
Find all critical points of , and use the second derivative test to classify each as a relative maximum, a relative minimum, or neither.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
51
The second derivative test reveals that has
A) a relative maximum only.
B) a relative minimum only.
C) a relative maximum and two relative minima.
D) neither a relative maximum nor a relative minimum.
A) a relative maximum only.
B) a relative minimum only.
C) a relative maximum and two relative minima.
D) neither a relative maximum nor a relative minimum.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
52
The second derivative test reveals that has
A) a relative maximum and two relative minima.
B) a relative maximum only.
C) a relative minimum only.
D) neither a relative maximum nor a relative minimum.
A) a relative maximum and two relative minima.
B) a relative maximum only.
C) a relative minimum only.
D) neither a relative maximum nor a relative minimum.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
53
A manufacturer estimates that if he produces x units of a particular commodity, the total cost will be dollars. For what value of x does the marginal cost satisfy ?

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
54
Name the vertical and horizontal asymptotes of the given graph. 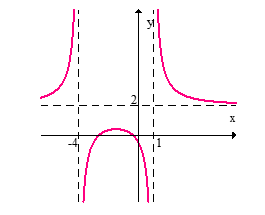
A) Vertical asymptotes: x = -4, x = 1; horizontal asymptote: y = 2
B) Vertical asymptotes: x = -4, x = 1; horizontal asymptotes: y = 2, y = 0
C) Vertical asymptotes: x = -4, x = 1, x = 0; horizontal asymptote: y = 2
D) Vertical asymptotes: x = -4, x = 1, x = 0; horizontal asymptotes: y = 2, y = 0

A) Vertical asymptotes: x = -4, x = 1; horizontal asymptote: y = 2
B) Vertical asymptotes: x = -4, x = 1; horizontal asymptotes: y = 2, y = 0
C) Vertical asymptotes: x = -4, x = 1, x = 0; horizontal asymptote: y = 2
D) Vertical asymptotes: x = -4, x = 1, x = 0; horizontal asymptotes: y = 2, y = 0

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
55
Find all vertical and horizontal asymptotes of the graph of the given function.
A) Vertical asymptotes: x = 5, x = 3, x = 2; horizontal asymptote: y = 0
B) Vertical asymptotes: x = 5, x = 3, x = 2; horizontal asymptote: y = 1
C) Vertical asymptotes: x = 5, x = 3; horizontal asymptote: y = 2
D) Vertical asymptotes: x = 5, x = 3; horizontal asymptote: y = 1
A) Vertical asymptotes: x = 5, x = 3, x = 2; horizontal asymptote: y = 0
B) Vertical asymptotes: x = 5, x = 3, x = 2; horizontal asymptote: y = 1
C) Vertical asymptotes: x = 5, x = 3; horizontal asymptote: y = 2
D) Vertical asymptotes: x = 5, x = 3; horizontal asymptote: y = 1

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
56
Graph .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
57
Graph .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
58
Graph .

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
59
Sketch the graph of the given function.
A)
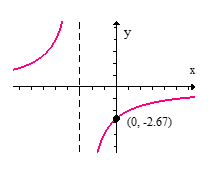
B)
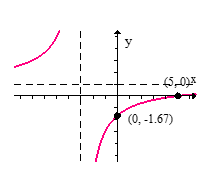
C)
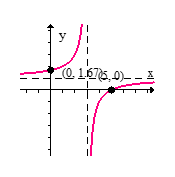
D)
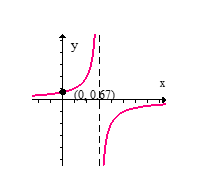
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
60
Find A and B so that the graph of has y = 11 as a horizontal asymptote and x = 2 as a vertical asymptote.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
61
Find the absolute maximum and minimum of on the interval -1 x 2.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
62
Determine the absolute maximum and minimum of on the interval -2 x 1.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
63
Find the absolute maximum and minimum of the function on the interval 0 x 3.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
64
Find the absolute maximum of the function on the interval .
A) 0
B)
C) -1
D) 1
A) 0
B)
C) -1
D) 1

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
65
Find the absolute minimum of the function on the interval -1 x 3.
A) -1
B) -4
C) 0
D) 3
A) -1
B) -4
C) 0
D) 3

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
66
Find the absolute minimum of the function on the interval 1 x 7.
A) -4
B) 0
C) 7
D) -1
A) -4
B) 0
C) 7
D) -1

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
67
Find the absolute maximum and absolute minimum of on the interval -2 x 5.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
68
The absolute minimum of the function on the interval 0 x 4 is 0.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
69
Find the absolute maximum and minimum of the function on the interval 0 x 2.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
70
Find the absolute maximum of the function on the interval -1 x 1.
A) 0
B) 1
C) -1
D) -2
A) 0
B) 1
C) -1
D) -2

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
71
Find the absolute maximum and absolute minimum of on the interval -1 x 2.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
72
Find the absolute maximum and absolute minimum of on the interval -9 x 4.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
73
= The absolute maximum of the function on the interval -1 x 2 is 11.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
74
=The absolute maximum of the function on the interval 0 x 1 is 1.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
75
The absolute minimum of on the interval 1 x 9 is 1.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
76
The cost of producing x units of a certain commodity is dollars. If the price is p(x) = (49 - x) dollars per unit, determine the level of production that maximizes profit.
A) x = 1
B) x = 2
C) x = 3
D) x = 6
A) x = 1
B) x = 2
C) x = 3
D) x = 6

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
77
A small manufacturing company estimates that the total cost in dollars of producing x radios per day is given by the formula . Find the number of units that will minimize the average cost.
A) 100
B) 147
C) 36
D) 71
A) 100
B) 147
C) 36
D) 71

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
78
Find the elasticity n of the demand function .
A)
B)
C) n = 4p
D)
A)
B)
C) n = 4p
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose the total cost of producing x units of a certain commodity is . Determine the largest and smallest values of the marginal cost for 0 x 5.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
80
The total cost of producing x units of a certain commodity is . Determine the minimum average cost of the commodity.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck


