Exam 3: Additional Applications of the Derivative
Exam 1: Functions, Graphs, and Limits154 Questions
Exam 2: Differentiation: Basic Concepts161 Questions
Exam 3: Additional Applications of the Derivative134 Questions
Exam 4: Exponential and Logarithmic Functions199 Questions
Exam 5: Integration167 Questions
Exam 6: Additional Topics in Integration111 Questions
Exam 7: Calculus of Several Variables113 Questions
Exam 8: Appendix: Algebra Review123 Questions
Select questions type
Find all vertical and horizontal asymptotes of the graph of the given function.
Free
(Short Answer)
4.8/5  (36)
(36)
Correct Answer:
Vertical asymptotes: x = -2, x = 3; horizontal asymptote: y = 1
A company that distributes landscape materials buys 4,000 tons of pine mulch a year. The ordering fee is $30 per shipment, the mulch costs them $20 per ton, and annual storage costs are $1.50 per ton. How many tons should be ordered in each shipment to minimize the total annual cost?
(Multiple Choice)
4.9/5  (28)
(28)
Find the absolute maximum and minimum of on the interval -1 x 2.
(Short Answer)
4.9/5  (34)
(34)
Find two non-negative numbers whose sum is 16 for which the product of their squares is as large as possible.
(Multiple Choice)
4.7/5  (33)
(33)
A 5-year projection of population trends suggests that t years from now, the population of a certain community will be thousand.
a. At what time during the 5-year period will the population be growing most rapidly?
b. At what time during the 5-year period will the population be growing least rapidly?
c. At what time is the rate of population growth changing most rapidly?
(Short Answer)
4.8/5  (28)
(28)
Find all intervals where the derivative of the function shown below is negative. 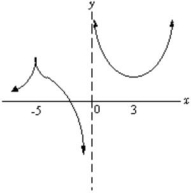
(Short Answer)
4.7/5  (33)
(33)
A manufacturer estimates that if he produces x units of a particular commodity, the total cost will be dollars. For what value of x does the marginal cost satisfy ?
(Short Answer)
4.8/5  (24)
(24)
Use the second derivative test to find the relative maxima and minima of the function .
(Multiple Choice)
4.7/5  (32)
(32)
Find the intervals of increase and decrease for the function .
(Multiple Choice)
4.8/5  (31)
(31)
Suppose the total cost of producing x units of a certain commodity is . Determine the largest and smallest values of the marginal cost for 0 x 5.
(Short Answer)
4.9/5  (30)
(30)
The total cost of producing x units of a certain commodity is . Determine the minimum average cost of the commodity.
(Short Answer)
4.9/5  (44)
(44)
Name the vertical and horizontal asymptotes of the given graph. 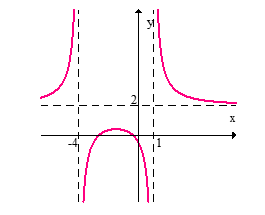
(Multiple Choice)
4.9/5  (41)
(41)
Showing 1 - 20 of 134
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)