Deck 13: Partial Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/104
Play
Full screen (f)
Deck 13: Partial Differentiation
1
Write the equation for the surface obtained by revolving the curve z = y2 (in the yz-plane) about the z-axis.
A) z = - x2 - y2
B) z = - x2 + y2
C) z = x2 - y2
D) z = x2 + y2
E) z = x + y2
A) z = - x2 - y2
B) z = - x2 + y2
C) z = x2 - y2
D) z = x2 + y2
E) z = x + y2
z = x2 + y2
2
Find the domain of the function f(x, y) = ln(9 - x2 - 9y2).
A)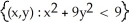
B)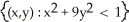
C)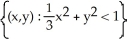
D)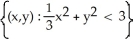
E)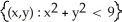
A)
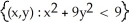
B)
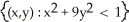
C)
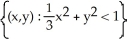
D)
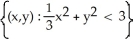
E)
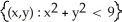
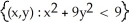
3
Find the domain of the function f(x) = 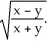
A) {(x, y) : x + y > 0}
B) {(x, y) : y -x and |x| |y|}
C) {(x, y) : y -x and y x}
D) {(x, y) : x + y > 0 and x - y > 0}
E) {(x, y) : x > 0 and y > 0}
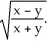
A) {(x, y) : x + y > 0}
B) {(x, y) : y -x and |x| |y|}
C) {(x, y) : y -x and y x}
D) {(x, y) : x + y > 0 and x - y > 0}
E) {(x, y) : x > 0 and y > 0}
{(x, y) : y -x and |x| |y|}
4
The set of all points (x,y) in the plane satisfying 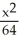 +
+ 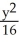 1 is the domain of which function?
1 is the domain of which function?
A) f(x,y) =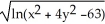
B) f(x,y) =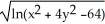
C) f(x,y) =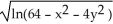
D) f(x,y) =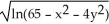
E) f(x,y) =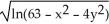
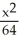 +
+ 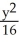 1 is the domain of which function?
1 is the domain of which function?A) f(x,y) =
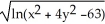
B) f(x,y) =
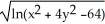
C) f(x,y) =
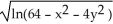
D) f(x,y) =
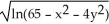
E) f(x,y) =
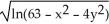

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
5
Describe the graph of the function f(x,y) = 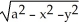 , where a > 0.
, where a > 0.
A) the sphere of radius a centred at the origin
B) the set of points inside or on the sphere of radius a centred at the origin
C) the points on the sphere of radius a centred at the origin that lie on or above the xy-plane
D) the circle centred at the origin in the xy-plane
E) the points inside or on the sphere of radius a centred at the origin that lie on or above the xy-plane
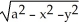 , where a > 0.
, where a > 0.A) the sphere of radius a centred at the origin
B) the set of points inside or on the sphere of radius a centred at the origin
C) the points on the sphere of radius a centred at the origin that lie on or above the xy-plane
D) the circle centred at the origin in the xy-plane
E) the points inside or on the sphere of radius a centred at the origin that lie on or above the xy-plane

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
6
Describe the level curves of the function f(x,y) = ![<strong>Describe the level curves of the function f(x,y) = , where a > 0.</strong> A) all circles in the xy-plane B) all circles in the xy-plane having centres at the origin. C) all circles in the xy-plane having centres at the origin and radii less than a D) the origin together with all circles in the xy-plane having centres at the origin and radii in the interval (0, a] E) a circle in the xy -plane having its centre at the origin and radius = a](https://storage.examlex.com/TB9661/11ee77e1_77b0_8c9e_a0f8_655f9b2f4676_TB9661_11.jpg) , where a > 0.
, where a > 0.
A) all circles in the xy-plane
B) all circles in the xy-plane having centres at the origin.
C) all circles in the xy-plane having centres at the origin and radii less than a
D) the origin together with all circles in the xy-plane having centres at the origin and radii in the interval (0, a]
E) a circle in the xy -plane having its centre at the origin and radius = a
![<strong>Describe the level curves of the function f(x,y) = , where a > 0.</strong> A) all circles in the xy-plane B) all circles in the xy-plane having centres at the origin. C) all circles in the xy-plane having centres at the origin and radii less than a D) the origin together with all circles in the xy-plane having centres at the origin and radii in the interval (0, a] E) a circle in the xy -plane having its centre at the origin and radius = a](https://storage.examlex.com/TB9661/11ee77e1_77b0_8c9e_a0f8_655f9b2f4676_TB9661_11.jpg) , where a > 0.
, where a > 0.A) all circles in the xy-plane
B) all circles in the xy-plane having centres at the origin.
C) all circles in the xy-plane having centres at the origin and radii less than a
D) the origin together with all circles in the xy-plane having centres at the origin and radii in the interval (0, a]
E) a circle in the xy -plane having its centre at the origin and radius = a

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
7
Let f(x, y, z) = x2 - y2 + z2 -1. The level surfaces f(x, y, z) = C, whereC < -1, are all hyperboloids of one sheet with centre at the origin.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
8
Describe the level curves f(x, y) = 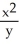 .
.
A) all parabolas in the xy-plane tangent to the x-axis at the origin
B) all parabolas in the xy-plane tangent to the y-axis at the origin
C) all parabolas in the xy-plane tangent to the y-axis
D) all parabolas in the xy-plane tangent to the x-axis
E) all parabolas in the xy-plane
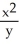 .
.A) all parabolas in the xy-plane tangent to the x-axis at the origin
B) all parabolas in the xy-plane tangent to the y-axis at the origin
C) all parabolas in the xy-plane tangent to the y-axis
D) all parabolas in the xy-plane tangent to the x-axis
E) all parabolas in the xy-plane

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
9
Which function f(x,y) has the level curves corresponding to c = -1, 0, and 1 shown in the figure below?
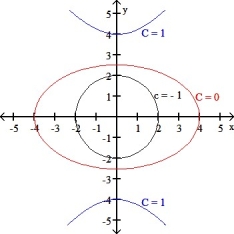
A) f(x,y) =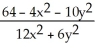
B) f(x,y) =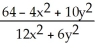
C) f(x,y) =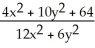
D) f(x,y) =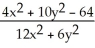
E) f(x,y) =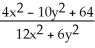

A) f(x,y) =
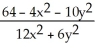
B) f(x,y) =
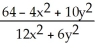
C) f(x,y) =
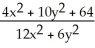
D) f(x,y) =
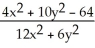
E) f(x,y) =
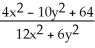

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
10
The graph below shows level curves f(x,y) = C for a function f and equally spaced values of C. Which of the following functions f is consistent with the graph?
(a) f(x,y) =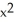 +
+ 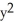 , (b) f(x,y) =
, (b) f(x,y) = 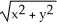 (c) f(x,y) =
(c) f(x,y) = 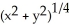
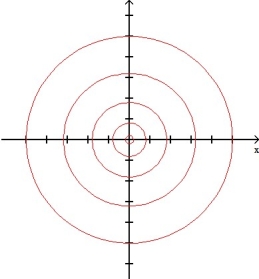
A) function (a)
B) function (b)
C) function (c)
D) all three functions
E) none of the functions
(a) f(x,y) =
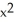 +
+ 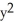 , (b) f(x,y) =
, (b) f(x,y) = 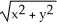 (c) f(x,y) =
(c) f(x,y) = 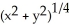

A) function (a)
B) function (b)
C) function (c)
D) all three functions
E) none of the functions

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
11
Identify the function f(x,y) whose domain is the shaded region shown in the figure below.
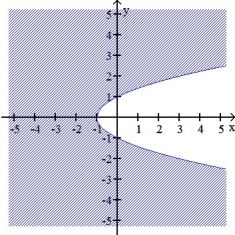
A) f(x,y) =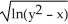
B) f(x,y) =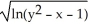
C) f(x,y) =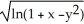
D) f(x,y) = )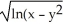
E) f(x,y) =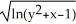

A) f(x,y) =
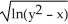
B) f(x,y) =
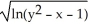
C) f(x,y) =
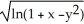
D) f(x,y) = )
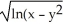
E) f(x,y) =
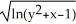

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
12
Describe the level surfaces of f(x, y, z) = 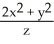 .
.
A) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the y-axis and eccentricity 1/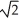
B) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the x-axis and eccentricity 1/ https://storage.examlex.com/TB9661/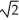 .
.
C) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the y-axis and eccentricity 1/2
D) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the y-axis and eccentricity 1/2.
E) none of the above
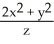 .
.A) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the y-axis and eccentricity 1/
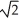
B) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the x-axis and eccentricity 1/ https://storage.examlex.com/TB9661/
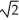 .
.C) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the y-axis and eccentricity 1/2
D) elliptic paraboloids symmetric about the z-axis and having horizontal cross-sections that are ellipses with major axis parallel to the y-axis and eccentricity 1/2.
E) none of the above

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the limit . 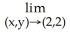
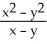
A) 1
B) 2
C) 4
D) The limit does not exist.
E) None of the above
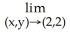
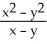
A) 1
B) 2
C) 4
D) The limit does not exist.
E) None of the above

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the limit . 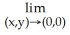
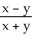
A) 0
B) 1
C) -1
D)
E) The limit does not exist.
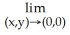
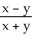
A) 0
B) 1
C) -1
D)
E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the limit. 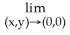
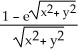
A) -2
B) 0
C) -1
D)
E) The limit does not exist.
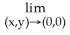
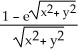
A) -2
B) 0
C) -1
D)
E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
16
Show that the function g(x,y) = 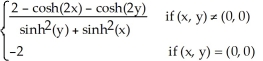 is continuous at (x, y) = (0, 0).
is continuous at (x, y) = (0, 0).
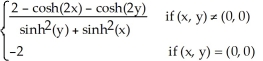 is continuous at (x, y) = (0, 0).
is continuous at (x, y) = (0, 0).
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
17
Let f(x,y) = 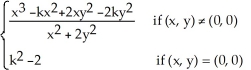 where k is a constant real number. Find all values of k so that the function f is continuousat (0, 0).
where k is a constant real number. Find all values of k so that the function f is continuousat (0, 0).
A) -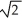 or
or 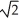
B) k R
R
C) -1 or 2
D) 1 or -2
E)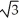 or -
or - 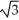
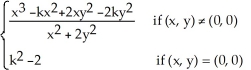 where k is a constant real number. Find all values of k so that the function f is continuousat (0, 0).
where k is a constant real number. Find all values of k so that the function f is continuousat (0, 0).A) -
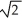 or
or 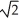
B) k
 R
RC) -1 or 2
D) 1 or -2
E)
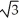 or -
or - 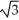

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the limit . 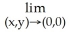
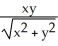
A) 1
B) 0
C)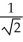
D) -1
E) The limit does not exist.
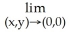
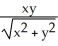
A) 1
B) 0
C)
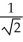
D) -1
E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the limit . 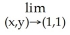
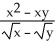
A) 0
B) 1
C) 2
D) -1
E) The limit does not exist.
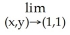
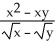
A) 0
B) 1
C) 2
D) -1
E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the limit . 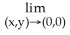
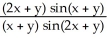
A) 1
B)
C) 0
D) 2
E) The limit does not exist.
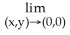
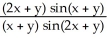
A) 1
B)

C) 0
D) 2
E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the limit. 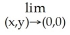
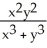
A) 0
B) 1
C) -1
D)
E) The limit does not exist.
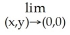
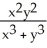
A) 0
B) 1
C) -1
D)
E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the limit 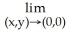
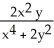 .
.
A) 0
B) 1
C)
D) -
E) The limit does not exist.
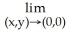
 .
.A) 0
B) 1
C)

D) -

E) The limit does not exist.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
23
Given z = f(x, y) = 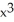 y -
y - 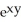 , find
, find 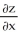 .
.
A) 3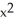 y -
y - 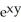
B) 3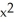 y - y
y - y 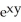
C)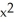 y - x
y - x 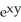
D)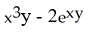
E)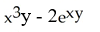
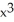 y -
y - 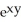 , find
, find 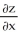 .
.A) 3
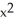 y -
y - 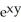
B) 3
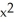 y - y
y - y 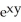
C)
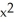 y - x
y - x 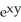
D)
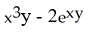
E)
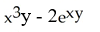

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
24
Given z = f(x, y) = 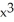 y -
y - 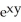 , find
, find 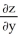 .
.
A)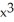 y - x
y - x 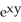
B)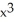 - y
- y 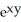
C)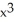 - x
- x 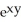
D)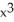 y -
y - 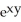
E) 3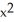 y - y
y - y 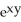
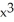 y -
y - 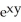 , find
, find 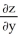 .
.A)
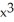 y - x
y - x 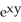
B)
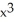 - y
- y 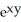
C)
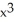 - x
- x 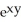
D)
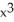 y -
y - 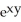
E) 3
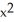 y - y
y - y 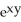

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
25
Find 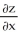 and
and 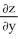 if z = f(x, y) = cos (ln(
if z = f(x, y) = cos (ln( 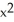 + xy +
+ xy + 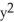 )).
)).
A)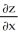 = -
= - 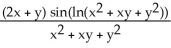 ;
; 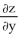 = -
= - 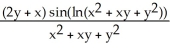
B)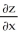 = -
= - 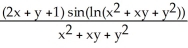 ;
; 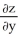 = -
= - 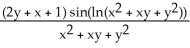
C)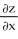 = -
= - 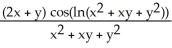 ;
; 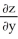 = -
= - 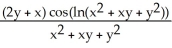
D)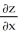 =
= 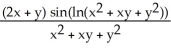 ;
; 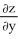 =
= 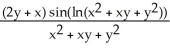
E)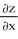 = -
= - 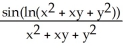 ;
; 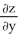 = -
= - 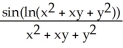
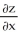 and
and 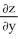 if z = f(x, y) = cos (ln(
if z = f(x, y) = cos (ln( 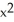 + xy +
+ xy + 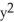 )).
)).A)
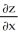 = -
= - 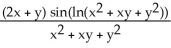 ;
; 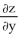 = -
= - 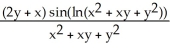
B)
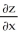 = -
= - 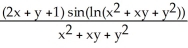 ;
; 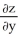 = -
= - 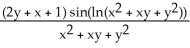
C)
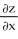 = -
= - 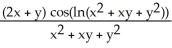 ;
; 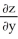 = -
= - 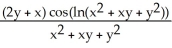
D)
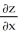 =
= 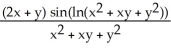 ;
; 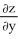 =
= 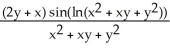
E)
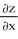 = -
= - 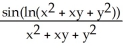 ;
; 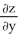 = -
= - 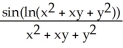

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
26
Find 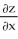 and
and 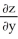 if z = f(x, y) =
if z = f(x, y) = 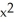
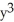 sin(x - 2y).
sin(x - 2y).
A)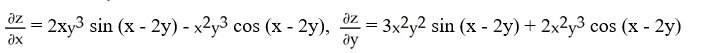
B)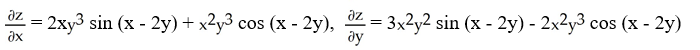
C)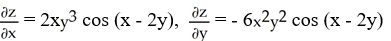
D)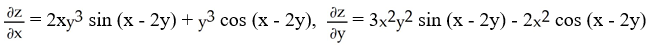
E)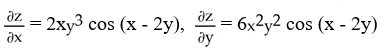
 and
and 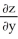 if z = f(x, y) =
if z = f(x, y) = 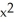
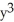 sin(x - 2y).
sin(x - 2y).A)
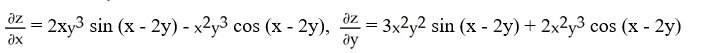
B)
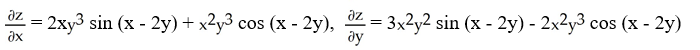
C)
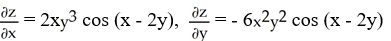
D)
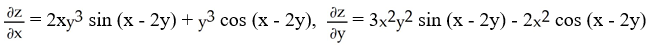
E)
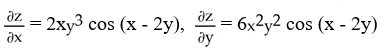

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
27
Find 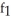 (3, 4) and
(3, 4) and 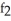 (3, 4) if f(x, y) = ln (x +
(3, 4) if f(x, y) = ln (x + 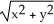 ).
).
A)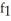 (3, 4) =
(3, 4) =  ,
, 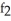 (3, 4) =
(3, 4) = 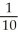
B)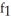 (3, 4) =
(3, 4) =  ,
, 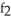 (3, 4) =
(3, 4) = 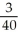
C)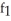 (3, 4) =
(3, 4) =  ,
, 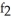 (3, 4) =
(3, 4) = 
D)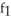 (3, 4) =
(3, 4) =  ,
, 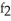 (3, 4) =
(3, 4) = 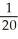
E)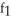 (3, 4) =
(3, 4) = 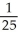 ,
, 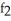 (3, 4) =
(3, 4) = 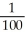
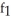 (3, 4) and
(3, 4) and 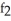 (3, 4) if f(x, y) = ln (x +
(3, 4) if f(x, y) = ln (x + 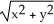 ).
).A)
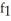 (3, 4) =
(3, 4) =  ,
, 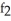 (3, 4) =
(3, 4) = 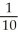
B)
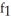 (3, 4) =
(3, 4) =  ,
, 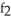 (3, 4) =
(3, 4) = 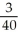
C)
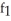 (3, 4) =
(3, 4) =  ,
, 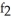 (3, 4) =
(3, 4) = 
D)
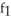 (3, 4) =
(3, 4) =  ,
, 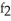 (3, 4) =
(3, 4) = 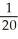
E)
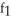 (3, 4) =
(3, 4) = 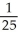 ,
,  (3, 4) =
(3, 4) = 

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate 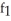 ( , - ln 6) if f(x, y) = cos (x
( , - ln 6) if f(x, y) = cos (x 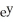 ).
).
A) -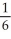
B) -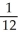
C)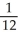
D)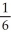
E)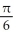
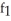 ( , - ln 6) if f(x, y) = cos (x
( , - ln 6) if f(x, y) = cos (x 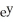 ).
).A) -
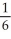
B) -
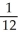
C)
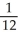
D)
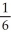
E)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
29
z = 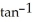 (y/x) + cos (x/y) satisfies the partial differential equationx
(y/x) + cos (x/y) satisfies the partial differential equationx 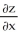 + y
+ y 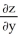 = 0 provided (x, y) (0, 0).
= 0 provided (x, y) (0, 0).
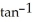 (y/x) + cos (x/y) satisfies the partial differential equationx
(y/x) + cos (x/y) satisfies the partial differential equationx 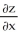 + y
+ y 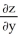 = 0 provided (x, y) (0, 0).
= 0 provided (x, y) (0, 0). 
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
30
Find the equation of the plane tangent to the surface 5x2 - 2y2 + 2z = - 9 and parallel to the plane 5x -4y + z = 2.
A)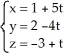 , t
, t 
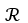
B) 5x - 4y + z = - 6
C) 10x -4y + 2 = 0
D) 5x - 4y + z = 9
E)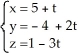 , t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 11ee7b4e_7d8e_093a_ae82_6552af45ee55_TB9661_11
, t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 11ee7b4e_7d8e_093a_ae82_6552af45ee55_TB9661_11
A)
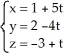 , t
, t 
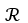
B) 5x - 4y + z = - 6
C) 10x -4y + 2 = 0
D) 5x - 4y + z = 9
E)
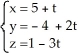 , t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 11ee7b4e_7d8e_093a_ae82_6552af45ee55_TB9661_11
, t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 11ee7b4e_7d8e_093a_ae82_6552af45ee55_TB9661_11
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
31
Find the slope of the tangent line to the curve that is the intersection of the surface z = x2 - y2 with the plane x = 2 at the point (2, 1, 3).
A) -2
B) 2
C) 0
D) -4
E) 4
A) -2
B) 2
C) 0
D) -4
E) 4

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
32
Find an equation of the plane tangent to the surface z = x2 - y2 at the point (2, 1, 3).
A) 4x - 2y + z = 9
B) 4x - 2y - z = 3
C) 4x + 2y + z = 13
D) 4x + 2y - z = 7
E) 4x - 2y + z = -9
A) 4x - 2y + z = 9
B) 4x - 2y - z = 3
C) 4x + 2y + z = 13
D) 4x + 2y - z = 7
E) 4x - 2y + z = -9

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
33
Find all points where the surface z = xy 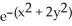 has a horizontal tangent plane.
has a horizontal tangent plane.
A)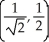 ,
, 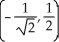 ,
, 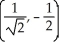 ,
, 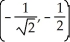 , (0, 0)
, (0, 0)
B)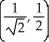 ,
, 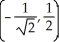 ,
, 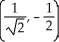 ,
, 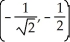
C)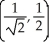 ,
, 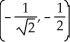 , (0, 0)
, (0, 0)
D)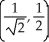 ,
, 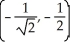
E) The tangent plane is never horizontal.
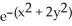 has a horizontal tangent plane.
has a horizontal tangent plane.A)
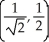 ,
, 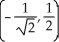 ,
, 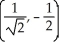 ,
, 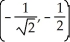 , (0, 0)
, (0, 0)B)
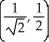 ,
, 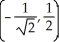 ,
, 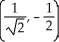 ,
, 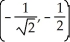
C)
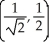 ,
, 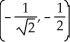 , (0, 0)
, (0, 0)D)
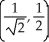 ,
, 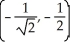
E) The tangent plane is never horizontal.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
34
Find all horizontal planes that are tangent to the surface z = x3 - 3xy2 + 6y2 + 1.
A) z = 1 and z = 3
B) z = 1
C) z = 3
D) z = -15
E) z = 9
A) z = 1 and z = 3
B) z = 1
C) z = 3
D) z = -15
E) z = 9

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
35
Find the equation of the tangent plane to the surface z = 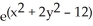 at the point(2, -2, 1).
at the point(2, -2, 1).
A) 4x - 8y - z = 23
B) 4x + 8y - z = -9
C) 4x - 8y + z = 25
D) 4x + 2y + z = 5
E) 4x - 8y - z = 9
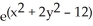 at the point(2, -2, 1).
at the point(2, -2, 1).A) 4x - 8y - z = 23
B) 4x + 8y - z = -9
C) 4x - 8y + z = 25
D) 4x + 2y + z = 5
E) 4x - 8y - z = 9

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
36
Find the equation of the normal line to the surface z = 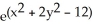 at the point(2, -2, 1).
at the point(2, -2, 1).
A)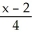 =
= 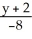 =
= 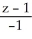
B)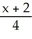 =
= 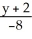 =
= 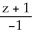
C)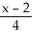 =
= 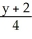 =
= 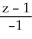
D)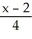 =
= 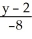 =
= 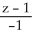
E)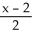 =
= 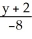 =
= 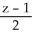
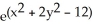 at the point(2, -2, 1).
at the point(2, -2, 1).A)
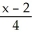 =
= 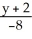 =
= 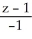
B)
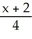 =
= 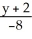 =
= 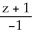
C)
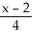 =
= 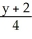 =
= 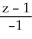
D)
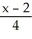 =
= 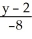 =
= 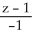
E)
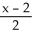 =
= 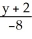 =
= 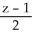

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
37
Find the distance from the point (0, 0, 1) to the surface z = x2 + 2y2.
A)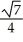 units
units
B)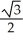 units
units
C) 2 units
D) unit
unit
E) 1 unit
A)
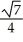 units
unitsB)
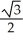 units
unitsC) 2 units
D)
 unit
unitE) 1 unit

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
38
Find f11(x, y) and f22(x, y) if f(x, y) = ex sin y + 2xy + y.
A) f11(x, y) =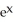 sin y + 2,
sin y + 2, 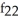 (x, y) =
(x, y) = 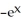 sin y
sin y
B) f11(x, y) =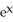 cos y, f22(x, y) =
cos y, f22(x, y) = 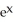 sin y
sin y
C) f11(x, y) =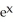 sin y, f22(x, y) =
sin y, f22(x, y) = 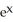 cos y
cos y
D) f11(x, y) =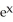 sin y, f22(x, y) =
sin y, f22(x, y) = 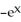 sin y
sin y
E) f11(x, y) =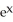 cos y, f22(x, y) =
cos y, f22(x, y) = 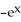 cos y
cos y
A) f11(x, y) =
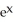 sin y + 2,
sin y + 2, 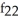 (x, y) =
(x, y) = 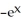 sin y
sin yB) f11(x, y) =
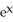 cos y, f22(x, y) =
cos y, f22(x, y) = 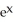 sin y
sin yC) f11(x, y) =
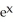 sin y, f22(x, y) =
sin y, f22(x, y) = 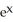 cos y
cos yD) f11(x, y) =
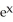 sin y, f22(x, y) =
sin y, f22(x, y) = 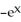 sin y
sin yE) f11(x, y) =
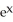 cos y, f22(x, y) =
cos y, f22(x, y) = 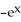 cos y
cos y
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
39
Find 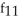 (x, y) and
(x, y) and 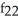 (x, y) if f(x, y) = ln
(x, y) if f(x, y) = ln 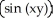 .
.
A)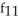 (x, y) = -
(x, y) = - 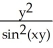 ,
,  (x, y) = -
(x, y) = - 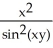
B) (x, y) = -
(x, y) = - 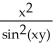 ,
, 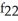 (x, y) = -
(x, y) = - 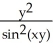
C)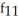 (x, y) = -
(x, y) = - 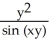 ,
, 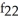 (x, y) = -
(x, y) = - 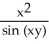
D)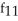 (x, y) = -
(x, y) = - 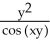 ,
, 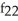 (x, y) = -
(x, y) = - 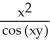
E)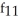 (x, y) = -
(x, y) = - 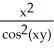 ,
, 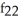 (x, y) = -
(x, y) = - 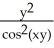
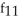 (x, y) and
(x, y) and 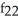 (x, y) if f(x, y) = ln
(x, y) if f(x, y) = ln 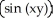 .
.A)
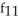 (x, y) = -
(x, y) = - 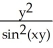 ,
, 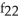 (x, y) = -
(x, y) = - 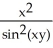
B)
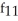 (x, y) = -
(x, y) = - 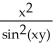 ,
, 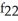 (x, y) = -
(x, y) = - 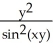
C)
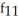 (x, y) = -
(x, y) = - 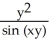 ,
, 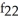 (x, y) = -
(x, y) = - 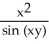
D)
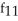 (x, y) = -
(x, y) = - 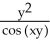 ,
, 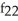 (x, y) = -
(x, y) = - 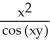
E)
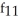 (x, y) = -
(x, y) = - 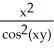 ,
, 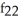 (x, y) = -
(x, y) = - 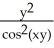

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
40
Find 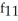 (x, y) and
(x, y) and 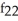 (x, y) if f(x, y) =
(x, y) if f(x, y) = 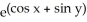 .
.
A) (x, y) =
(x, y) = 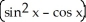
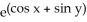 ;
; 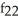 (x, y) =
(x, y) = 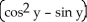
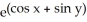
B)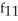 (x, y) =
(x, y) = 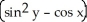
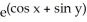 ;
; 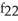 (x, y) =
(x, y) = 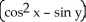
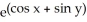
C)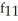 (x, y) =
(x, y) = 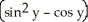
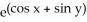 ;
; 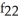 (x, y) =
(x, y) = 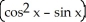
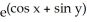
D)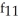 (x, y) =
(x, y) = 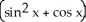
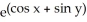 ;
; 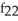 (x, y) =
(x, y) = 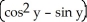
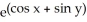
E)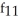 (x, y) =
(x, y) = 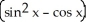
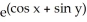 ;
; 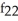 (x, y) =
(x, y) = 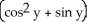
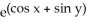
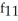 (x, y) and
(x, y) and 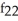 (x, y) if f(x, y) =
(x, y) if f(x, y) = 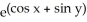 .
.A)
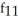 (x, y) =
(x, y) = 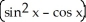
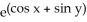 ;
; 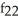 (x, y) =
(x, y) = 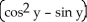
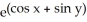
B)
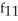 (x, y) =
(x, y) = 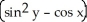
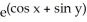 ;
; 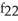 (x, y) =
(x, y) = 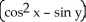
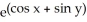
C)
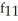 (x, y) =
(x, y) = 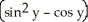
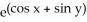 ;
; 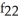 (x, y) =
(x, y) = 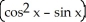
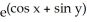
D)
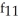 (x, y) =
(x, y) = 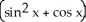
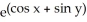 ;
; 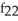 (x, y) =
(x, y) = 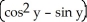
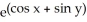
E)
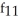 (x, y) =
(x, y) = 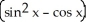
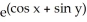 ;
; 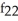 (x, y) =
(x, y) = 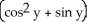

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
41
Find 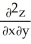 if z =
if z = 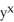 .
.
A) x(x - 1)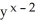
B) x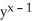 ln(x)
ln(x)
C) x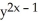 ln(y)
ln(y)
D)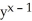 (1 + xln(y))
(1 + xln(y))
E)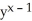 (1 + xln(x - 1))
(1 + xln(x - 1))
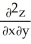 if z =
if z = 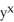 .
.A) x(x - 1)
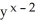
B) x
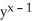 ln(x)
ln(x)C) x
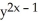 ln(y)
ln(y)D)
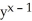 (1 + xln(y))
(1 + xln(y))E)
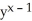 (1 + xln(x - 1))
(1 + xln(x - 1))
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
42
Find 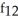 (x, y) and
(x, y) and 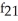 (x, y) if f(x, y) = ln
(x, y) if f(x, y) = ln 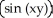 .
.
A)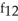 (x, y) =
(x, y) = 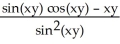 ;
; 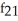 (x, y) =
(x, y) = 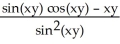
B) (x, y) =
(x, y) = 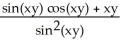 ;
; 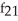 (x, y) =
(x, y) = 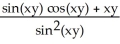
C)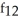 (x, y) = 1 -
(x, y) = 1 - 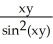 ;
; 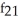 (x, y) = 1 +
(x, y) = 1 + 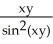
D) (x, y) =
(x, y) = 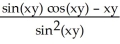 ;
;  (x, y) =
(x, y) = 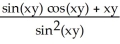
E)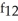 (x, y) =
(x, y) = 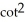 (xy) -
(xy) - 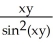 ;
; 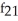 (x, y) =
(x, y) = 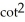 (xy) +
(xy) + 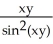
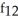 (x, y) and
(x, y) and 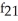 (x, y) if f(x, y) = ln
(x, y) if f(x, y) = ln 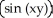 .
.A)
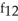 (x, y) =
(x, y) = 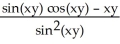 ;
; 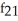 (x, y) =
(x, y) = 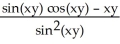
B)
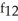 (x, y) =
(x, y) = 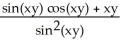 ;
; 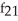 (x, y) =
(x, y) = 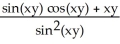
C)
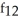 (x, y) = 1 -
(x, y) = 1 - 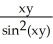 ;
; 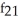 (x, y) = 1 +
(x, y) = 1 + 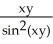
D)
 (x, y) =
(x, y) = 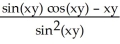 ;
; 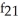 (x, y) =
(x, y) = 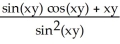
E)
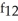 (x, y) =
(x, y) = 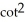 (xy) -
(xy) - 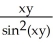 ;
;  (x, y) =
(x, y) = 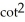 (xy) +
(xy) + 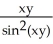

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
43
Find the value of the positive constant real number k such that the function 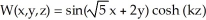 is harmonic for all points in 3-space.
is harmonic for all points in 3-space.
A)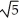
B) 2 -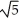
C) 2
D) 2 +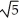
E) 3
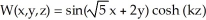 is harmonic for all points in 3-space.
is harmonic for all points in 3-space.A)
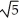
B) 2 -
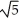
C) 2
D) 2 +
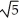
E) 3

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
44
Compute 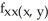 and
and 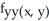 if f(x, y) = xy + sin xy + x2 + 5xln y.
if f(x, y) = xy + sin xy + x2 + 5xln y.
A)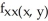 =
=  sin xy + 2,
sin xy + 2, 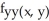 = -
= -  sin xy -
sin xy - 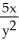
B)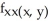 = -
= - 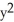 sin xy + 2,
sin xy + 2, 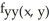 = -
= - 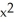 sin xy -
sin xy - 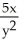
C)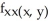 = -
= - 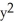 sin xy + 2,
sin xy + 2, 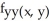 =
= 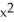 sin xy -
sin xy - 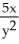
D)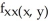 = -
= - 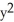 sin xy + 2,
sin xy + 2, 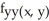 = -
= - 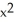 sin xy +
sin xy + 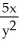
E)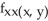 = -
= - 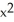 sin xy + 2,
sin xy + 2, 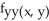 = -
= - 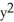 sin xy -
sin xy - 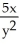
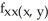 and
and 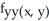 if f(x, y) = xy + sin xy + x2 + 5xln y.
if f(x, y) = xy + sin xy + x2 + 5xln y.A)
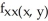 =
= 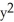 sin xy + 2,
sin xy + 2, 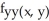 = -
= - 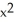 sin xy -
sin xy - 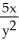
B)
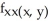 = -
= - 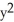 sin xy + 2,
sin xy + 2, 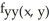 = -
= - 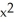 sin xy -
sin xy - 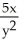
C)
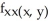 = -
= - 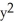 sin xy + 2,
sin xy + 2, 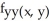 =
= 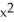 sin xy -
sin xy - 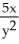
D)
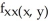 = -
= - 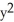 sin xy + 2,
sin xy + 2, 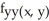 = -
= - 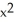 sin xy +
sin xy + 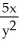
E)
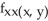 = -
= - 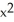 sin xy + 2,
sin xy + 2, 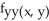 = -
= - 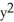 sin xy -
sin xy - 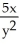

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
45
Calculate and simplify 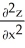 +
+ 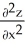 if z =
if z = 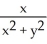 .
.
A) -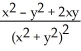
B)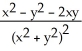
C)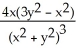
D) 0
E)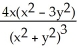
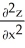 +
+ 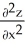 if z =
if z = 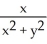 .
.A) -
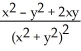
B)
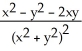
C)
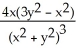
D) 0
E)
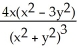

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
46
Let F(x,y) = 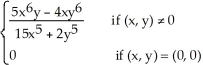 (a) Use the definitions of partial derivatives to calculate
(a) Use the definitions of partial derivatives to calculate 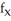 (0, 0) and
(0, 0) and 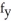 (0, 0).
(0, 0).
(b) Calculate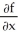 and
and 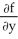 for (x, y) ≠ (0, 0).
for (x, y) ≠ (0, 0).
(c) Use part (b) and the definitions of partial derivatives to calculate the mixed partial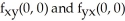 .
.
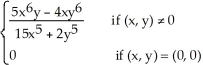 (a) Use the definitions of partial derivatives to calculate
(a) Use the definitions of partial derivatives to calculate 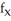 (0, 0) and
(0, 0) and 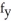 (0, 0).
(0, 0).(b) Calculate
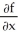 and
and 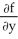 for (x, y) ≠ (0, 0).
for (x, y) ≠ (0, 0).(c) Use part (b) and the definitions of partial derivatives to calculate the mixed partial
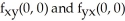 .
.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate 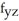 (3, 2, 1) if f(x, y, z) = x
(3, 2, 1) if f(x, y, z) = x 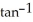 (yz).
(yz).
A)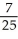
B) -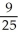
C) -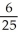
D)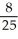
E) 0
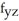 (3, 2, 1) if f(x, y, z) = x
(3, 2, 1) if f(x, y, z) = x 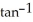 (yz).
(yz).A)
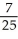
B) -
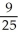
C) -
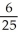
D)
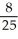
E) 0

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
48
Find 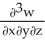 if w =
if w = 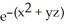 .
.
A) 2x(1 - yz)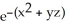
B) 2x(1 + yz)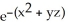
C) x(1 - yz)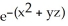
D) 2(1 + yz)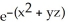
E) 2(1 - yz)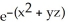
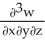 if w =
if w = 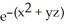 .
.A) 2x(1 - yz)
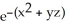
B) 2x(1 + yz)
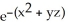
C) x(1 - yz)
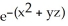
D) 2(1 + yz)
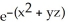
E) 2(1 - yz)
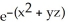

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
49
Calculate and simplify ut - uxx - uyy for the function u = 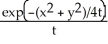 .
.
A) -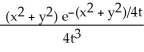
B)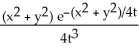
C)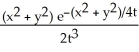
D) 0
E) -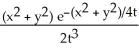
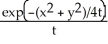 .
.A) -
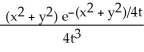
B)
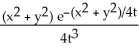
C)
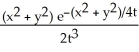
D) 0
E) -
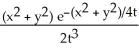

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
50
For what value(s) of the constant k is the function f(x, y, z) = 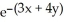 sin(kz) a harmonic function in 3-space? Note that a harmonic function f in 3-space satisfies
sin(kz) a harmonic function in 3-space? Note that a harmonic function f in 3-space satisfies 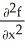 +
+ 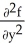 +
+ 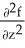 = 0.
= 0.
A) k = 7
B) k = ± 1
C) k = ± 5
D) k = 0
E) k = ±4
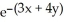 sin(kz) a harmonic function in 3-space? Note that a harmonic function f in 3-space satisfies
sin(kz) a harmonic function in 3-space? Note that a harmonic function f in 3-space satisfies 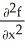 +
+ 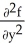 +
+ 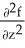 = 0.
= 0.A) k = 7
B) k = ± 1
C) k = ± 5
D) k = 0
E) k = ±4

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
51
Find 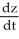 if z = x sin y, where x = t2 + 2t + 1 and y = ln t.
if z = x sin y, where x = t2 + 2t + 1 and y = ln t.
A)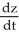 = 2(t + 1) sin(ln t) +
= 2(t + 1) sin(ln t) + 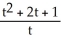 cos(ln t)
cos(ln t)
B)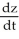 = 2(t + 1) sin(t) +
= 2(t + 1) sin(t) + 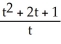 cos(t)
cos(t)
C)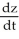 = 2(t + 1) sin(ln t) -
= 2(t + 1) sin(ln t) - 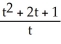 sin(ln t)
sin(ln t)
D)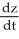 = 2(t + 1) cos(ln t) +
= 2(t + 1) cos(ln t) + 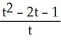 sin(ln t)
sin(ln t)
E)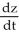 = 2(t + 1) sin(ln t) +
= 2(t + 1) sin(ln t) + 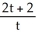 cos(ln t)
cos(ln t)
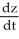 if z = x sin y, where x = t2 + 2t + 1 and y = ln t.
if z = x sin y, where x = t2 + 2t + 1 and y = ln t.A)
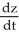 = 2(t + 1) sin(ln t) +
= 2(t + 1) sin(ln t) + 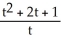 cos(ln t)
cos(ln t)B)
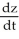 = 2(t + 1) sin(t) +
= 2(t + 1) sin(t) + 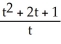 cos(t)
cos(t)C)
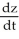 = 2(t + 1) sin(ln t) -
= 2(t + 1) sin(ln t) - 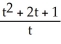 sin(ln t)
sin(ln t)D)
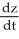 = 2(t + 1) cos(ln t) +
= 2(t + 1) cos(ln t) + 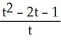 sin(ln t)
sin(ln t)E)
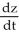 = 2(t + 1) sin(ln t) +
= 2(t + 1) sin(ln t) + 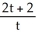 cos(ln t)
cos(ln t)
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
52
Find 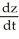 if z =
if z = 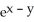 , where x = ln t and y = ln t2.
, where x = ln t and y = ln t2.
A)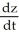 = -
= - 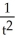
B)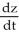 =
= 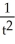
C)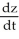 = -
= - 
D)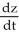 =
= 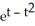
E)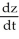 = -
= - 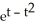
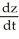 if z =
if z = 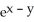 , where x = ln t and y = ln t2.
, where x = ln t and y = ln t2.A)
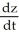 = -
= - 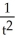
B)
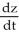 =
= 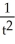
C)
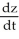 = -
= - 
D)
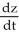 =
= 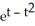
E)
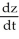 = -
= - 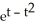

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
53
Find 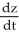 if z = sin(uv)cos(uv), where u = et and y = e2t.
if z = sin(uv)cos(uv), where u = et and y = e2t.
A) 3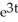
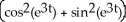
B) 3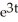
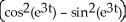
C) 3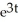
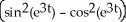
D)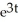
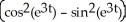
E)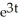
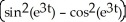
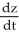 if z = sin(uv)cos(uv), where u = et and y = e2t.
if z = sin(uv)cos(uv), where u = et and y = e2t.A) 3
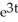
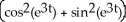
B) 3
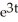
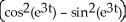
C) 3
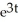
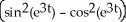
D)
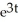
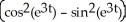
E)
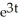
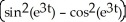

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
54
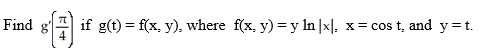
A)
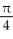 - ln (
- ln ( 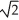 )
)B)
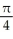 + ln (
+ ln ( 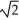 )
)C) -
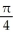 + ln (
+ ln ( 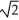 )
)D) -
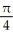 - ln (
- ln ( 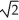 )
)E)
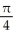 + ln (2)
+ ln (2)
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
55
Let h(t) = f(x, y), where f(x, y) = 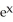 +
+ 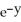 , x = t, y = t2. Find
, x = t, y = t2. Find 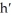 (2).
(2).
A)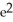 - 2
- 2 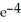
B)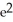 + 4
+ 4 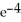
C)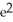 - 4
- 4 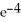
D)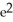 + 2
+ 2 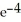
E)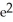 - 4
- 4 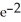
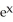 +
+ 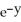 , x = t, y = t2. Find
, x = t, y = t2. Find 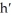 (2).
(2).A)
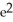 - 2
- 2 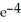
B)
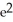 + 4
+ 4 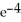
C)
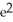 - 4
- 4 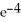
D)
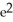 + 2
+ 2 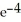
E)
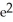 - 4
- 4 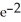

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
56
Let z = f(x, y), where x = u 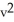 , and y =
, and y =  . Use the chain rule to find
. Use the chain rule to find 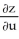 at (u, v) = (2,- 1) given that
at (u, v) = (2,- 1) given that 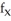 (2,- 1) = - 7,
(2,- 1) = - 7, 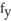 (2,- 1) = 5,
(2,- 1) = 5, 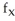 (2,- 2) = 3, and
(2,- 2) = 3, and 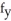 (2,- 2) = -2.
(2,- 2) = -2.
A) -5
B) 4
C) -12
D) 5
E) 2
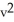 , and y =
, and y =  . Use the chain rule to find
. Use the chain rule to find 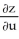 at (u, v) = (2,- 1) given that
at (u, v) = (2,- 1) given that 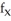 (2,- 1) = - 7,
(2,- 1) = - 7, 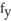 (2,- 1) = 5,
(2,- 1) = 5, 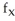 (2,- 2) = 3, and
(2,- 2) = 3, and 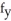 (2,- 2) = -2.
(2,- 2) = -2.A) -5
B) 4
C) -12
D) 5
E) 2

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
57
If W = 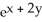 , where x = t + sin(t) and y = 2t -1, then the value of
, where x = t + sin(t) and y = 2t -1, then the value of 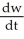 at t = 0 is equal to:
at t = 0 is equal to:
A)
B)
C)
D)
E) 0
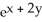 , where x = t + sin(t) and y = 2t -1, then the value of
, where x = t + sin(t) and y = 2t -1, then the value of 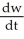 at t = 0 is equal to:
at t = 0 is equal to:A)

B)

C)

D)

E) 0

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
58
Let g be a function of a single variable having continuous second order derivatives, and letu(x, y) = g(y + mx) , for some constant real number m. Determine all values of m such that u(x, y) satisfies the partial differential equation 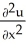 - 10
- 10 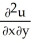 + 24
+ 24 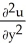 = 0.
= 0.
A) - 2 and 12
B) - 4 and - 6
C) 2 and - 12
D) 4 and 6
E) 3 and 8
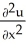 - 10
- 10 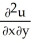 + 24
+ 24 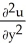 = 0.
= 0.A) - 2 and 12
B) - 4 and - 6
C) 2 and - 12
D) 4 and 6
E) 3 and 8

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
59
Use the chain rule to find the values of 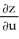 and
and 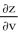 . at (u, v) = (0, 1), where z = x3y5,x = u - v, and y = u + v.
. at (u, v) = (0, 1), where z = x3y5,x = u - v, and y = u + v.
A)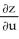 = -2;
= -2; 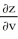 = -8
= -8
B)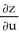 = 8;
= 8; 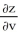 = 2
= 2
C)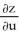 = -2;
= -2; 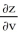 = 8
= 8
D)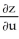 = -8;
= -8; 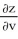 = -2
= -2
E)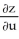 = 2;
= 2; 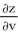 = 8
= 8
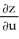 and
and 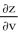 . at (u, v) = (0, 1), where z = x3y5,x = u - v, and y = u + v.
. at (u, v) = (0, 1), where z = x3y5,x = u - v, and y = u + v.A)
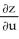 = -2;
= -2; 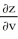 = -8
= -8B)
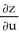 = 8;
= 8; 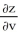 = 2
= 2C)
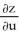 = -2;
= -2; 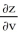 = 8
= 8D)
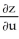 = -8;
= -8; 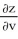 = -2
= -2E)
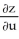 = 2;
= 2; 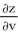 = 8
= 8
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
60
Assuming that the function f has continuous first partial derivatives 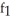 and
and 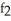 , calculate and simplify
, calculate and simplify 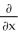 f(x2y, x
f(x2y, x 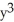 ).
).
A)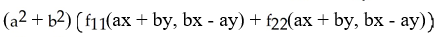
B)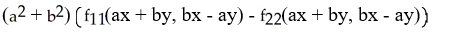
C)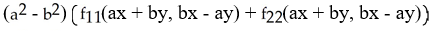
D)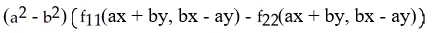
E)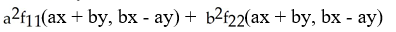
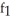 and
and 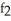 , calculate and simplify
, calculate and simplify 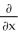 f(x2y, x
f(x2y, x 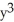 ).
).A)
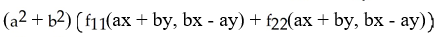
B)
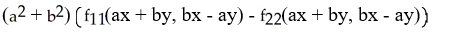
C)
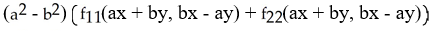
D)
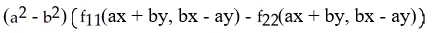
E)
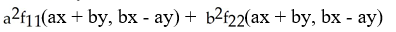

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
61
Assuming that the function f has continuous second partial derivatives and that a and b are constants, calculate and simplify 
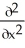 +
+ 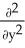
 f(ax + by, bx - ay).
f(ax + by, bx - ay).
A)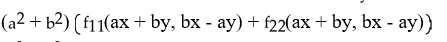
B)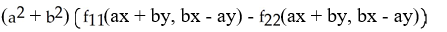
C)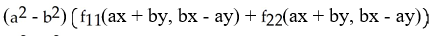
D)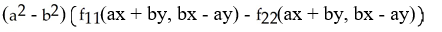
E)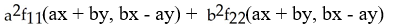

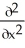 +
+ 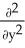
 f(ax + by, bx - ay).
f(ax + by, bx - ay).A)
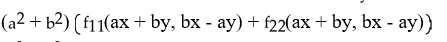
B)
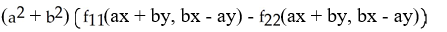
C)
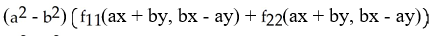
D)
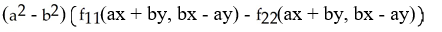
E)
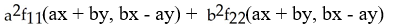

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
62
Assuming that the function f has continuous partial derivatives of orders 1 and 2, calculate and simplify 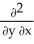 f(
f( 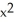 y, x
y, x 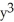 ).
).
A)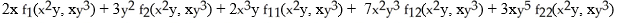
B)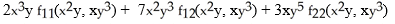
C)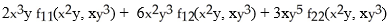
D)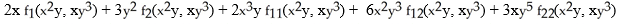
E)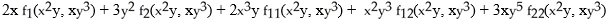
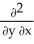 f(
f( 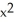 y, x
y, x 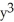 ).
).A)
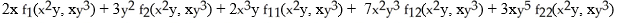
B)
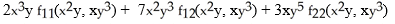
C)
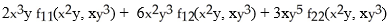
D)
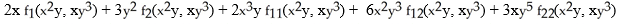
E)
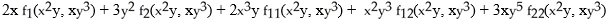

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
63
Let z = f(x,y) = 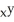 + y where x =
+ y where x = 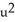 +
+ 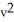 -4 and y = uv -1. Find the value of
-4 and y = uv -1. Find the value of 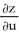 at (u , v) = (2 , -1).
at (u , v) = (2 , -1).
A) -2
B) -8
C) -10
D) 0
E) -13
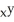 + y where x =
+ y where x = 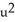 +
+ 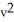 -4 and y = uv -1. Find the value of
-4 and y = uv -1. Find the value of 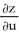 at (u , v) = (2 , -1).
at (u , v) = (2 , -1).A) -2
B) -8
C) -10
D) 0
E) -13

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
64
Find the linearization L(x,y) of f(x,y) = x 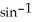 (y) about the point
(y) about the point 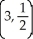 .
.
A)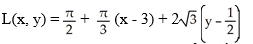
B)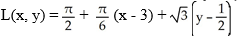
C)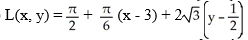
D)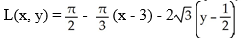
E)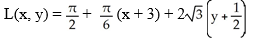
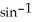 (y) about the point
(y) about the point 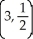 .
.A)
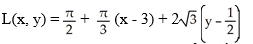
B)
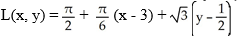
C)
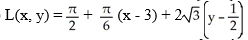
D)
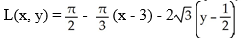
E)
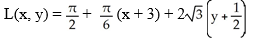

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
65
The linearization of f(x,y) =ln (x2 + y2 + xy) at the point (1,-1) is given by
A) L(x,y) = ln(x - y - 2)
B) L(x, y) = x - y - 2
C) L(x, y) = x - y + 2
D) L(x, y) = x - y
E) L(x, y) = 3x - y - 4
A) L(x,y) = ln(x - y - 2)
B) L(x, y) = x - y - 2
C) L(x, y) = x - y + 2
D) L(x, y) = x - y
E) L(x, y) = 3x - y - 4

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
66
Use the linearization of f(x,y) = x3 e-y about the point (2, 0) to find an approximate value for f(2.1, 0.1).
A) 8.4
B) 10.0
C) 9.2
D) 7.6
E) 6.3
A) 8.4
B) 10.0
C) 9.2
D) 7.6
E) 6.3

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
67
Find the differential of the function f(x, y) = . 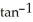
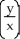
A)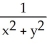 (y dx + x dy)
(y dx + x dy)
B)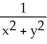 (y dx - x dy)
(y dx - x dy)
C) -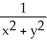 (y dx + x dy)
(y dx + x dy)
D) -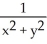 (y dx - x dy)
(y dx - x dy)
E) -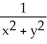 (y dy - x dx)
(y dy - x dx)
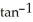
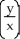
A)
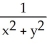 (y dx + x dy)
(y dx + x dy)B)
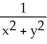 (y dx - x dy)
(y dx - x dy)C) -
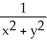 (y dx + x dy)
(y dx + x dy)D) -
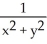 (y dx - x dy)
(y dx - x dy)E) -
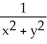 (y dy - x dx)
(y dy - x dx)
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
68
The pressure P, the volume V, and the temperature T (in Kelvin) of a confined gas are related by the ideal gas law P V = kT , where k is a constant. If P = 0.5 pascal when V = 50 cm3 and T = 360 K, determine by approximately what percentage P changes if V and T change to52 cm3 and 351 K, respectively.
A) 6.5 %
B) 1.5 %
C) -4.5 %
D) -6.5 %
E) -1.5 %
A) 6.5 %
B) 1.5 %
C) -4.5 %
D) -6.5 %
E) -1.5 %

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
69
The area of a triangle is given by the formula A =  ab sin , where is the angle between the sides having lengths a and b. If measurements indicate that a = 4 m with error ± 1 cm,b = 3 m with error ± 1 cm, and = 60° with error ± 2°, use differentials to determine the approximate maximum error in the calculated area of the triangle.
ab sin , where is the angle between the sides having lengths a and b. If measurements indicate that a = 4 m with error ± 1 cm,b = 3 m with error ± 1 cm, and = 60° with error ± 2°, use differentials to determine the approximate maximum error in the calculated area of the triangle.
A) about 0.135 m2
B) about 6.015 m2
C) about 0.603 m2
D) about 0.014 m2
E) about 0.862 m2
 ab sin , where is the angle between the sides having lengths a and b. If measurements indicate that a = 4 m with error ± 1 cm,b = 3 m with error ± 1 cm, and = 60° with error ± 2°, use differentials to determine the approximate maximum error in the calculated area of the triangle.
ab sin , where is the angle between the sides having lengths a and b. If measurements indicate that a = 4 m with error ± 1 cm,b = 3 m with error ± 1 cm, and = 60° with error ± 2°, use differentials to determine the approximate maximum error in the calculated area of the triangle.A) about 0.135 m2
B) about 6.015 m2
C) about 0.603 m2
D) about 0.014 m2
E) about 0.862 m2

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
70
When the ellipse b2x2 + a2y2 = a2b2 is rotated about the x-axis, the volume V of the spheroid is 4 ab2/3. If a and b are each increased by 1%, use differentials to find the approximate percentage change in V.
A) increase of 1%
B) increase of 2%
C) increase of 3%
D) increase of 4%
E) increase of 5%
A) increase of 1%
B) increase of 2%
C) increase of 3%
D) increase of 4%
E) increase of 5%

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
71
In an electric circuit the current measured in amperes is related to the voltage and the resistance by Ohm's Law V = IR. If the voltage V drops from 24 to 23 volts and the resistance R drops from 100 to 80 Ohms, use differentials to determine whether the current I will increase or decrease and by approximately how much?
A) decrease of 0.067 amps
B) increase of 0.094 amps
C) increase of 0.038 amps
D) decrease of 0.028 amps
E) decrease of 0.062 amps
A) decrease of 0.067 amps
B) increase of 0.094 amps
C) increase of 0.038 amps
D) decrease of 0.028 amps
E) decrease of 0.062 amps

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
72
Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x2 + xy, y2 - ln(z)).
A)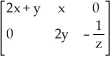
B)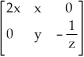
C)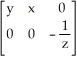
D)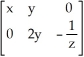
E)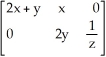
A)
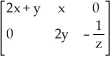
B)
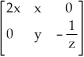
C)
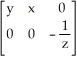
D)
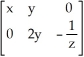
E)
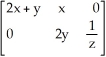

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
73
Use the Jacobian matrix for the transformation f(x, y, z) = 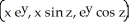 to find an approximate value for f(1.98, 0.03, -0.01).
to find an approximate value for f(1.98, 0.03, -0.01).
A) (2.00, -0.02, 0.03)
B) (2.04, -0.02, 0.03)
C) (2.02, 0.02, 0.97)
D) (1.98, 0.02, -0.03)
E) (2, 0, 0)
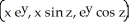 to find an approximate value for f(1.98, 0.03, -0.01).
to find an approximate value for f(1.98, 0.03, -0.01).A) (2.00, -0.02, 0.03)
B) (2.04, -0.02, 0.03)
C) (2.02, 0.02, 0.97)
D) (1.98, 0.02, -0.03)
E) (2, 0, 0)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
74
Find a unit vector in the direction of which the function f(x, y) = 6 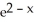 sin
sin 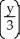 (a) increases most rapidly, and (b) decreases most rapidly at the point (2, ).
(a) increases most rapidly, and (b) decreases most rapidly at the point (2, ).
A) (a)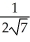 (3
(3 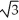 i - j) (b)
i - j) (b) 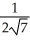 (-3
(-3 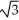 i + j)
i + j)
B) (a)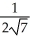 (3
(3 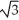 i + j) (b) -
i + j) (b) - 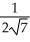 (3
(3 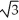 i + j)
i + j)
C) (a) -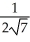 (3
(3 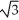 i + j) (b)
i + j) (b) 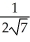 (3
(3 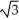 i + j)
i + j)
D) (a)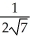 (-3
(-3 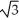 i + j) (b)
i + j) (b) 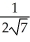 (3
(3 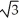 i - j)
i - j)
E) (a)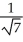 (3
(3 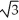 i - j) (b)
i - j) (b) 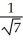 (-3
(-3 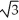 i + j)
i + j)
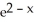 sin
sin 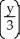 (a) increases most rapidly, and (b) decreases most rapidly at the point (2, ).
(a) increases most rapidly, and (b) decreases most rapidly at the point (2, ).A) (a)
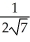 (3
(3 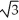 i - j) (b)
i - j) (b) 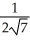 (-3
(-3 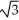 i + j)
i + j)B) (a)
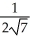 (3
(3 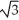 i + j) (b) -
i + j) (b) - 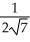 (3
(3 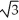 i + j)
i + j)C) (a) -
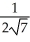 (3
(3 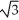 i + j) (b)
i + j) (b) 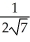 (3
(3 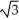 i + j)
i + j)D) (a)
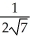 (-3
(-3 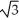 i + j) (b)
i + j) (b) 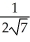 (3
(3 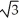 i - j)
i - j)E) (a)
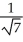 (3
(3 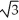 i - j) (b)
i - j) (b) 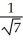 (-3
(-3 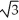 i + j)
i + j)
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
75
Find the directional derivative of f(x, y) = 3x2 + 2xy - 7y2 at the point (-1, 3) in the direction making an angle of 60° with the positive x- and y-axes.
A) -2 - 30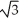
B) -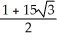
C) 1 - 15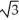
D) -1 - 15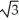
E) 1 -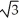
A) -2 - 30
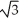
B) -
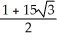
C) 1 - 15
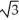
D) -1 - 15
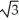
E) 1 -
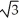

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
76
Calculate the directional derivative of the function 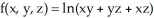 at (1, 1, 1) in the direction from (1, 1, 1) toward the point (-1, -2, 3).
at (1, 1, 1) in the direction from (1, 1, 1) toward the point (-1, -2, 3).
A) -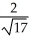
B)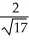
C)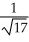
D) -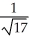
E) -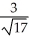
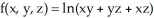 at (1, 1, 1) in the direction from (1, 1, 1) toward the point (-1, -2, 3).
at (1, 1, 1) in the direction from (1, 1, 1) toward the point (-1, -2, 3).A) -
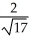
B)
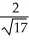
C)
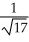
D) -
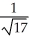
E) -
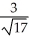

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
77
Let f(x, y, z) = 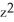 -2
-2 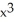 - 3y + 4 and let P be the point (1, -1, 3). Which of the following statements is false?
- 3y + 4 and let P be the point (1, -1, 3). Which of the following statements is false?
A)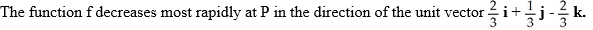
B) The maximum rate of change of f at P is 9.
C) There is no direction in which the rate of change of f at P is equal to 10.
D) There is a direction in which the rate of change of f at P is equal to -12.
E) The function f increases most rapidly at P in the direction of the vector -6 i - 3 j + 6 k.
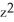 -2
-2 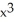 - 3y + 4 and let P be the point (1, -1, 3). Which of the following statements is false?
- 3y + 4 and let P be the point (1, -1, 3). Which of the following statements is false?A)
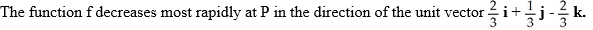
B) The maximum rate of change of f at P is 9.
C) There is no direction in which the rate of change of f at P is equal to 10.
D) There is a direction in which the rate of change of f at P is equal to -12.
E) The function f increases most rapidly at P in the direction of the vector -6 i - 3 j + 6 k.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
78
At the point (1, 2) the function f(x, y) has a directional derivative of 2 in the direction toward (2, 2) and a directional derivative of -2 in the direction toward (1, 1). Find the directional derivative of f at (1, 2) in the direction toward the point (4, 6).
A) -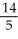
B) -
C)
D)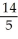
E) 4
A) -
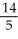
B) -

C)

D)
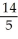
E) 4

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
79
The temperature in the xy-plane is a function T(x, y). At the point (a,b) the directional derivative of T in the direction of the vector 3 i + 4 j is 4 and the directional derivative in the direction of 5 i - 12 j is -2. Find 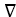 T(a,b).
T(a,b).
A)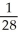 (68 i + 89 j)
(68 i + 89 j)
B)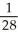 (43 i - 17 j)
(43 i - 17 j)
C)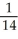 (-53 i + 117 j)
(-53 i + 117 j)
D)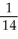 (28 i + 37 j)
(28 i + 37 j)
E) - (172 i + 89 j)
(172 i + 89 j)
 T(a,b).
T(a,b).A)
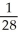 (68 i + 89 j)
(68 i + 89 j)B)
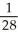 (43 i - 17 j)
(43 i - 17 j)C)
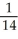 (-53 i + 117 j)
(-53 i + 117 j)D)
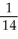 (28 i + 37 j)
(28 i + 37 j)E) -
 (172 i + 89 j)
(172 i + 89 j)
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
80
Find an equation of the tangent plane to the surface x2 + 2y2 + 3z2 = 6 at the point(1, 1, 1).
A) x + y + z = 3
B) x + 4y + 9z = 14
C) x + 2y + 3z = 6
D) 3x + 2y + z = 6
E) x + 2y - 3z = 6
A) x + y + z = 3
B) x + 4y + 9z = 14
C) x + 2y + 3z = 6
D) 3x + 2y + z = 6
E) x + 2y - 3z = 6

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck


