Exam 13: Partial Differentiation
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Use the chain rule to find the values of 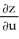 and
and 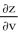 . at (u, v) = (0, 1), where z = x3y5,x = u - v, and y = u + v.
. at (u, v) = (0, 1), where z = x3y5,x = u - v, and y = u + v.
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
A
Find the Maclaurin series of the function exy-3y by using Taylor series for functions of one variable.
Free
(Multiple Choice)
4.7/5  (31)
(31)
Correct Answer:
A
Which function f(x,y) has the level curves corresponding to c = -1, 0, and 1 shown in the figure below?
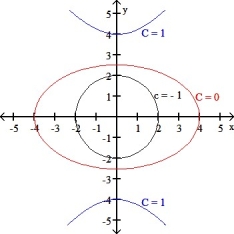
(Multiple Choice)
4.9/5  (36)
(36)
The equations x = u2 - v2 and y = 2uv define u and v as functions of x and y in a neighbourhood of the point where u = 2 and v = 1. Evaluate 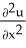 at that point.
at that point.
(Multiple Choice)
4.7/5  (28)
(28)
The pressure P, the volume V, and the temperature T (in Kelvin) of a confined gas are related by the ideal gas law P V = kT , where k is a constant. If P = 0.5 pascal when V = 50 cm3 and T = 360 K, determine by approximately what percentage P changes if V and T change to52 cm3 and 351 K, respectively.
(Multiple Choice)
4.8/5  (30)
(30)
Calculate and simplify ut - uxx - uyy for the function u = 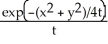 .
.
(Multiple Choice)
4.9/5  (37)
(37)
The temperature in the xy-plane is a function T(x, y). At the point (a,b) the directional derivative of T in the direction of the vector 3 i + 4 j is 4 and the directional derivative in the direction of 5 i - 12 j is -2. Find 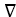 T(a,b).
T(a,b).
(Multiple Choice)
4.8/5  (34)
(34)
Find f11(x, y) and f22(x, y) if f(x, y) = ex sin y + 2xy + y.
(Multiple Choice)
4.9/5  (33)
(33)
Use the linearization of f(x,y) = x3 e-y about the point (2, 0) to find an approximate value for f(2.1, 0.1).
(Multiple Choice)
4.7/5  (39)
(39)
Let h(t) = f(x, y), where f(x, y) = 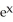 +
+ 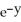 , x = t, y = t2. Find
, x = t, y = t2. Find 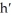 (2).
(2).
(Multiple Choice)
4.9/5  (40)
(40)
Find the Maclaurin polynomial of degree 5 for the function f(x, y) = cos(x - y2).
(Multiple Choice)
5.0/5  (39)
(39)
Find the domain of the function f(x, y) = ln(9 - x2 - 9y2).
(Multiple Choice)
4.7/5  (31)
(31)
The directional derivative of a function F(x,y) at a point P in the direction of the unit vector-  i +
i +  j is equal to -4, while the directional derivative at P in the direction of the unit vector
j is equal to -4, while the directional derivative at P in the direction of the unit vector 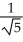 i+
i+ 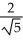 j is equal to0. The value of
j is equal to0. The value of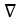 F(P) is equal to:
F(P) is equal to:
(Multiple Choice)
4.7/5  (35)
(35)
Find the equation of the plane tangent to the surface 5x2 - 2y2 + 2z = - 9 and parallel to the plane 5x -4y + z = 2.
(Multiple Choice)
4.8/5  (35)
(35)
z = 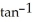 (y/x) + cos (x/y) satisfies the partial differential equationx
(y/x) + cos (x/y) satisfies the partial differential equationx 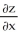 + y
+ y 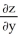 = 0 provided (x, y) (0, 0).
= 0 provided (x, y) (0, 0).
(True/False)
4.8/5  (38)
(38)
Showing 1 - 20 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)