Deck 5: More Applications of Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/130
Play
Full screen (f)
Deck 5: More Applications of Differentiation
1
A balloon is 100 metres off the ground and rising vertically at the constant rate of 3 metres per second just as an automobile passes beneath it travelling along a straight, level road at the constant rate of 72 kilometres per hour. How fast is the distance between them changing one second later? (rounded to the nearest hundredth of a metre)
A) 6.76 metres per second
B) 43.71 metres per second
C) 20.22 metres per second
D) 10.00 metres per second
E) 1.28 metres per second
A) 6.76 metres per second
B) 43.71 metres per second
C) 20.22 metres per second
D) 10.00 metres per second
E) 1.28 metres per second
6.76 metres per second
2
An aircraft is climbing at a 30-degree angle to the horizontal. How fast is the aircraft gaining altitude if its speed is 750 kilometres per hour?
A) 400 kilometres per hour
B) 350 kilometres per hour
C) 375 kilometres per hour
D) 250 kilometres per hour
E) 425 kilometres per hour
A) 400 kilometres per hour
B) 350 kilometres per hour
C) 375 kilometres per hour
D) 250 kilometres per hour
E) 425 kilometres per hour
375 kilometres per hour
3
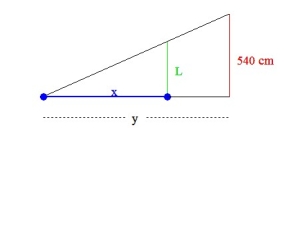
A lamp is shining on top of a vertical light post that is 540 centimetres tall. A girl is running away from the base of the light post at a constant rate so that her shadow is increasing at the rate of 15 cm/s and the tip of her shadow is moving away from the base at the rate of 90 cm/s. How tall is she?
Let x be length of shadow, y be the distance from the tip of the shadow to the base of the light post and L be the girl's height (as shown in the figure below).
From similarity,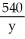 =
= 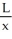 ; hence 540 x = L y; L is a constant!
; hence 540 x = L y; L is a constant!
Differentiating both sides with respect to time we obtain 540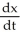 = L
= L 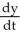
Substituting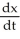 = rate of change of shadow = +15 cm / s and
= rate of change of shadow = +15 cm / s and
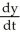 = rate of change of distance between the tip of the shadow and the base of the light post = +
= rate of change of distance between the tip of the shadow and the base of the light post = +
90 cm /s, we obtain 540(15) = L (90). Therefore
L =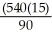 = 90 cm.
= 90 cm.
The girl is 90 cm tall (about 3 feet ).
From similarity,
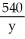 =
= 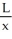 ; hence 540 x = L y; L is a constant!
; hence 540 x = L y; L is a constant!Differentiating both sides with respect to time we obtain 540
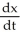 = L
= L 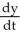
Substituting
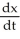 = rate of change of shadow = +15 cm / s and
= rate of change of shadow = +15 cm / s and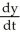 = rate of change of distance between the tip of the shadow and the base of the light post = +
= rate of change of distance between the tip of the shadow and the base of the light post = + 90 cm /s, we obtain 540(15) = L (90). Therefore
L =
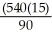 = 90 cm.
= 90 cm.The girl is 90 cm tall (about 3 feet ).

4
A plane flying horizontally at an altitude of 1 kilometre and a speed of 500 kilometres per hour passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing at the instant when the plane is 2 kilometres away from the station.
A) 350 kilometres per hour
B) 462 kilometres per hour
C) 402 kilometres per hour
D) 433 kilometres per hour
E) 382 kilometres per hour
A) 350 kilometres per hour
B) 462 kilometres per hour
C) 402 kilometres per hour
D) 433 kilometres per hour
E) 382 kilometres per hour

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
5
A water trough is 10 m long and has vertical cross-sections perpendicular to its long axis with the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height of 50 cm. If the trough is being filled with water at the rate of 0.2 cubic metres per minute, how fast is the water level rising when the water is 30 cm deep?
A)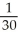 m/min
m/min
B)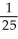 m/min
m/min
C)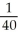 m/min
m/min
D)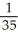 m/min
m/min
E)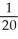 m/min
m/min
A)
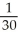 m/min
m/minB)
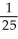 m/min
m/minC)
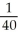 m/min
m/minD)
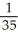 m/min
m/minE)
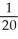 m/min
m/min
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
6
Water is leaking out of an inverted conical tank at a rate of 0.1 cubic metres per minute at the same time the water is being pumped into the tank at a constant rate. The tank has height 6 metres and the diameter at the top is 4 metres. If the water level is rising at a rate of 20 centimetres per minute, find the rate at which water is being pumped into the tank at the instant when the water is 2 metres deep.
A) 0.179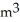 /min
/min
B) 0.279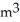 /min
/min
C) 0.379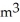 /min
/min
D) 0.479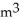 /min
/min
E) 0.365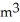 /min
/min
A) 0.179
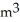 /min
/minB) 0.279
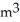 /min
/minC) 0.379
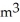 /min
/minD) 0.479
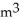 /min
/minE) 0.365
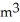 /min
/min
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
7
A boat is pulled toward a dock by a rope with one end attached to the bow of the boat and the other end passing through a ring attached to the dock 2 metres higher than the bow of the boat. If the rope is pulled in at the rate of 0.5 metres per second, how fast is the boat approaching the dock when 3 metres of rope are out? (round to the nearest hundredth metre)
A) 1.15 metres per second
B) 0.67 metres per second
C) 2.38 metres per second
D) 0.97 metres per second
E) 1.68 metres per second
A) 1.15 metres per second
B) 0.67 metres per second
C) 2.38 metres per second
D) 0.97 metres per second
E) 1.68 metres per second

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
8
In a classical equation from chemistry, the pressure of a gas is proportional to the product of the volume of the gas and the temperature of the gas. In symbols, P = kVT for some constant k. How fast is the pressure changing at an instant when the volume is 20 mL and increasing at 3 mL/min and the temperature is at 21 degrees C and is decreasing at a rate of 2 degrees per minute? Assume that k = 0.8 kilograms per mL-degree.
A) increasing at 18.4 kilograms/min
B) increasing at 14.4 kilograms/min
C) decreasing at 23.5 kilograms/min
D) decreasing at 12.8 kilograms/min
E) increasing at 12.7 kilograms/min
A) increasing at 18.4 kilograms/min
B) increasing at 14.4 kilograms/min
C) decreasing at 23.5 kilograms/min
D) decreasing at 12.8 kilograms/min
E) increasing at 12.7 kilograms/min

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
9
At a certain instant the length of one leg of a right triangle is 6 m and is increasing at 2 m/min while the length of the other leg is 8 m and is decreasing at 3 m/min. How fast is the area of the triangle changing at that instant?
A) decreasing at 1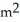 /min
/min
B) decreasing at 2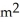 /min
/min
C) unchanging, holding steady
D) increasing at 2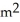 /min
/min
E) increasing at 1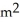 /min
/min
A) decreasing at 1
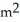 /min
/minB) decreasing at 2
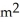 /min
/minC) unchanging, holding steady
D) increasing at 2
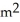 /min
/minE) increasing at 1
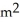 /min
/min
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
10
The power P (watts) in an electric circuit is related to the circuit's resistance R (ohms) and the current I (amperes) by the equation P = R I2. If the power of a circuit is a constant 40 watts and the resistance R is decreasing at the constant rate of 4 ohms /s, at what rate is the current I changing at the instant the current is 2 amperes?
A) The current is decreasing at the rate of amperes / s.
amperes / s.
B) The current is increasing at the rate of amperes / s.
amperes / s.
C) The current is decreasing at the rate of amperes / s.
amperes / s.
D) The current is increasing at the rate of amperes / s.
amperes / s.
E) The current is decreasing at the rate of amperes / s.
amperes / s.
A) The current is decreasing at the rate of
 amperes / s.
amperes / s.B) The current is increasing at the rate of
 amperes / s.
amperes / s.C) The current is decreasing at the rate of
 amperes / s.
amperes / s.D) The current is increasing at the rate of
 amperes / s.
amperes / s.E) The current is decreasing at the rate of
 amperes / s.
amperes / s.
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
11
A lamp is 3 metres high on a post located 5 metres from a vertical wall. A 2 metre tall man walks toward the wall from the lamppost on a path perpendicular to the wall. He is walking at a rate of 1 metre per second. When he is 1 metre from the wall, how fast is the shadow of his head moving up the wall?
A) 0.31 metres per second
B) 0.52 metres per second
C) 1.29 metres per second
D) 0.96 metres per second
E) 0.36 metres per second
A) 0.31 metres per second
B) 0.52 metres per second
C) 1.29 metres per second
D) 0.96 metres per second
E) 0.36 metres per second

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
12
The height of a right circular cylinder is increasing at the rate of 4 cm/s and its radius is decreasing at the rate of 2 cm/s. At what rate is the lateral surface area of the cylinder changing when the height is 3 centimetres and the radius is 1 centimetre?
The lateral surface area of a cylinder of base radius r and height h is given by S = 2 r h
A) decreasing at 16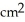 /s
/s
B) decreasing at 4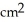 /s
/s
C) increasing at 4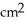 /s
/s
D) increasing at 20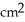 /s
/s
E) increasing at 16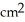 /s
/s
The lateral surface area of a cylinder of base radius r and height h is given by S = 2 r h
A) decreasing at 16
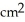 /s
/sB) decreasing at 4
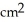 /s
/sC) increasing at 4
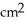 /s
/sD) increasing at 20
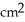 /s
/sE) increasing at 16
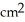 /s
/s
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
13
A plane is flying horizontally at an altitude of seven kilometres and a speed of 800 kilometres per hour. At time t = 0 the plane passes over a tracking station on the ground. How fast is the angle of elevation of the plane as measured at the tracking station changing 18 seconds later?
A) increasing at 86 rad/h
B) increasing at 66 rad/h
C) decreasing at 86 rad/h
D) decreasing at 66 rad/h
E) decreasing at 62 rad/h
A) increasing at 86 rad/h
B) increasing at 66 rad/h
C) decreasing at 86 rad/h
D) decreasing at 66 rad/h
E) decreasing at 62 rad/h

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
14
Water is leaking out of an inverted conical cup at a rate of 2 cubic centimetres per second. The radius of the cone is six centimetres and the height is 10 centimetres. Find the rate at which the water depth is changing at time t when the depth of the water is 3 centimetres.
A) decreasing at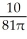 cm/sec
cm/sec
B) decreasing at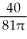 cm/sec
cm/sec
C) decreasing at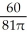 cm/sec
cm/sec
D) decreasing at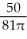 cm/sec
cm/sec
E) decreasing at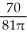 cm/sec
cm/sec
A) decreasing at
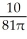 cm/sec
cm/secB) decreasing at
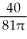 cm/sec
cm/secC) decreasing at
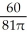 cm/sec
cm/secD) decreasing at
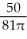 cm/sec
cm/secE) decreasing at
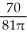 cm/sec
cm/sec
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
15
Find 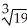 correct to four decimal places using Newton's Method.
correct to four decimal places using Newton's Method.
A) 2.6672
B) 2.6627
C) 2.6698
D) 2.6684
E) 2.6667
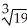 correct to four decimal places using Newton's Method.
correct to four decimal places using Newton's Method.A) 2.6672
B) 2.6627
C) 2.6698
D) 2.6684
E) 2.6667

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
16
Find the roots of the equation x3 - 5x - 3 = 0 correct to three decimal places using Newton's Method.
A) -1.834, -0.657, 2.491
B) -1.834, 0.657, 2.491
C) -1.824, -0.667, -2.501
D) -1.824, -0.667, 2.589
E) -1.834, -0.667, 2.491
A) -1.834, -0.657, 2.491
B) -1.834, 0.657, 2.491
C) -1.824, -0.667, -2.501
D) -1.824, -0.667, 2.589
E) -1.834, -0.667, 2.491

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
17
Find the solution of the equation 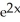 + 5x = 0 to four decimal places using Newton's Method.
+ 5x = 0 to four decimal places using Newton's Method.
A) 0.1486
B) -0.2486
C) -0.1486
D) -0.1506
E) -0.1473
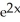 + 5x = 0 to four decimal places using Newton's Method.
+ 5x = 0 to four decimal places using Newton's Method.A) 0.1486
B) -0.2486
C) -0.1486
D) -0.1506
E) -0.1473

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
18
Find the roots of the equation ln x - 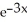 = 0 to four decimal places using Newton's Method.
= 0 to four decimal places using Newton's Method.
A) 1.2445
B) 1.9445
C) 1.3445
D) 1.0445
E) 1.0543
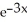 = 0 to four decimal places using Newton's Method.
= 0 to four decimal places using Newton's Method.A) 1.2445
B) 1.9445
C) 1.3445
D) 1.0445
E) 1.0543

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
19
Find the solutions of the equation cos x - x4 = 0 to 4 decimal places using Newton's Method.
A) 0.8241, -0.6421
B) 0.8906, -0.8906
C) 0.8241, -0.8241
D) 0.6421, -0.6421
E) 0.8954, -0.8954
A) 0.8241, -0.6421
B) 0.8906, -0.8906
C) 0.8241, -0.8241
D) 0.6421, -0.6421
E) 0.8954, -0.8954

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
20
Newton's Method with initial approximation x0 is used to approximate a real root of the equation x4 - 2 = 0. The value of Newton's Method iteration x1 is equal to
A)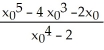
B)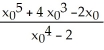
C)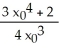
D)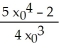
E) ±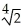
A)
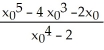
B)
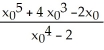
C)
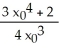
D)
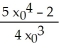
E) ±
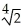

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
21
Use Newton's Method to find the x coordinate of a point on the curve y = x3 + 1 such that the tangent line to the curve at that point passes through the point (2, 0). Give your answer accurate to three decimal places.
A) 3.061
B) 3.050
C) 3.054
D) 3.058
E) 3.049
A) 3.061
B) 3.050
C) 3.054
D) 3.058
E) 3.049

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
22
Use Newton's Method to find the solution of the equation x + tan x = 0 on the interval [2, 3] accurate to four decimal places.
A) 2.0288
B) 2.0293
C) 2.0278
D) 2.0272
E) 2.0284
A) 2.0288
B) 2.0293
C) 2.0278
D) 2.0272
E) 2.0284

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
23
Newton's Method with the initial approximation x1 = 1 is used to approximate the real root of the equation x3 + 3x - 1 = 0. Determine the value of x3, the third iteration of Newton's Method.
A)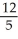
B)
C)
D)
E)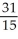
A)
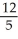
B)

C)

D)

E)
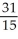

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
24
The function f(x) = ( 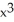 - 5)
- 5) 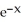 has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function.
has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function.
A) 3.4023
B) 3.2240
C) 3.1278
D) 3.4259
E) none of the above
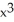 - 5)
- 5) 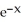 has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function.
has one critical point in the interval x > 0. Find this critical point with error within 0.005 by applying Newton's Method to an appropriate function.A) 3.4023
B) 3.2240
C) 3.1278
D) 3.4259
E) none of the above

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
25
Find all the roots of the equation sin x = x2.
A) ± 0.876726
B) 0.876726
C) 0.876833
D) 0, 0.876726
E) 0, 0.876833
A) ± 0.876726
B) 0.876726
C) 0.876833
D) 0, 0.876726
E) 0, 0.876833

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
26
Give the iteration formula for finding the roots of the equation sin x - x2 = 0 using Newton's Method.
A)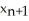 =
= 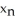 -
- 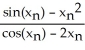
B)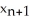 =
= 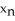 -
- 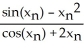
C)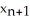 =
= 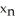 +
+ 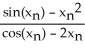
D)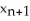 =
= 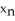 -
- 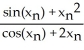
E)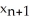 =
= 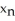 +
+ 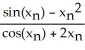
A)
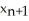 =
= 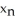 -
- 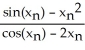
B)
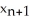 =
= 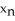 -
- 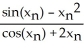
C)
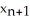 =
= 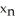 +
+ 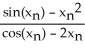
D)
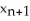 =
= 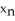 -
- 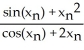
E)
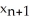 =
= 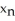 +
+ 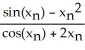

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
27
Use Newton's Method to find the roots of the equation cos x = x.
A) 0.739335
B) 0.739161
C) 0.739085
D) 0.739204
E) 0.739185
A) 0.739335
B) 0.739161
C) 0.739085
D) 0.739204
E) 0.739185

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
28
Suppose Newton's Method applied to f(x) = 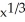 is used to "find"the root of the equation
is used to "find"the root of the equation 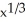 = 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
= 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
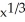 is used to "find"the root of the equation
is used to "find"the root of the equation 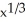 = 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
= 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root? 
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
29
By considering the locations of its critical points, determine how many real zeros the function 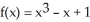 must have. Find them, correct to six decimal places.
must have. Find them, correct to six decimal places.
A) one zero, -1.624717
B) one zero, -1.424717
C) one zero, -1.324717
D) three zeros, -1.424717, -0.436712, and 0.688212
E) two zeros, -1.424717, and -0.436712
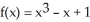 must have. Find them, correct to six decimal places.
must have. Find them, correct to six decimal places.A) one zero, -1.624717
B) one zero, -1.424717
C) one zero, -1.324717
D) three zeros, -1.424717, -0.436712, and 0.688212
E) two zeros, -1.424717, and -0.436712

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate . 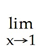
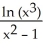
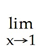
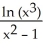

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate . 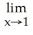
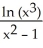
A)
B)
C)
D)
E)
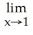
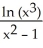
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
32
Use the table of values below to evaluate 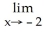
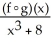
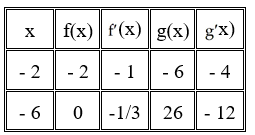
A) -
B) - 2
C)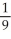
D) -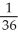
E)
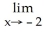
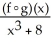

A) -

B) - 2
C)
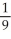
D) -
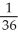
E)


Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the limit . 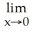
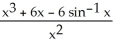
A) 3
B) 0
C) -3
D) 1
E)
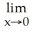
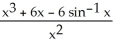
A) 3
B) 0
C) -3
D) 1
E)

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate . 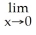
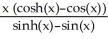
A) -1
B)
C) 3
D) 1
E) -
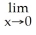
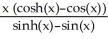
A) -1
B)
C) 3
D) 1
E) -

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate the limit . 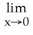
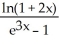
A) 1
B)
C) 0
D)
E)
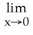
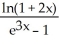
A) 1
B)

C) 0
D)
E)


Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the limit 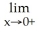 x ln x.
x ln x.
A) -
B) 1
C) 0
D)
E) -1
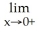 x ln x.
x ln x.A) -
B) 1
C) 0
D)
E) -1

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate . 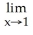
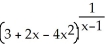
A) 1
B) e
C)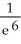
D)
E) -6
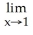
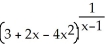
A) 1
B) e
C)
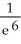
D)
E) -6

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate the limit . 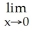
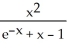
A) -2
B) 2
C) 0
D) 1
E) -1
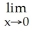
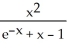
A) -2
B) 2
C) 0
D) 1
E) -1

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the limit . 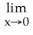
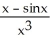
A)
B)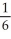
C) 1
D)
E)
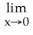
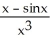
A)

B)
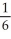
C) 1
D)

E)


Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the limit . 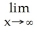
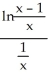
A) -2
B) -1
C) 0
D)
E) 1
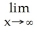
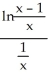
A) -2
B) -1
C) 0
D)
E) 1

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the limit . 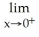
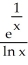
A) -
B)
C) 1
D) 0
E) -1
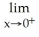
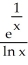
A) -
B)
C) 1
D) 0
E) -1

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the limit 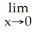 .
. 
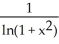 -
- 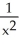

A)
B)
C)
D) 1
E) -
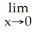 .
. 
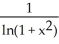 -
- 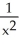

A)

B)

C)

D) 1
E) -


Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate 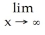 x ( - 2
x ( - 2 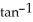 (7x)).
(7x)).
A)
B) 0
C)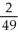
D) -
E)
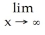 x ( - 2
x ( - 2 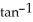 (7x)).
(7x)).A)

B) 0
C)
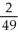
D) -

E)

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
44
Evaluate the limit . 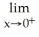
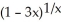
A) -
B) -3
C)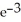
D) -ln 3
E)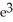
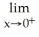
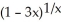
A) -

B) -3
C)
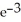
D) -ln 3
E)

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the limit . 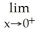
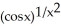
A)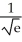
B) 1
C)
D) -
E) -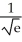
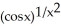
A)
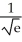
B) 1
C)

D) -

E) -
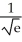

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
46
Find all local extreme values of the function f(x) = 2 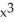 + 3
+ 3 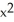 - 12x + 13 and their locations.
- 12x + 13 and their locations.
A) local maximum 33 at x = -2, local minimum 26 at x = 1
B) local maximum 26 at x = -2, local minimum 33 at x = 1
C) local maximum 26 at x = -1, local minimum 17 at x = 2
D) local maximum 17 at x = -1, local minimum 26 at x = 2
E) no local extrema
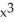 + 3
+ 3 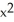 - 12x + 13 and their locations.
- 12x + 13 and their locations.A) local maximum 33 at x = -2, local minimum 26 at x = 1
B) local maximum 26 at x = -2, local minimum 33 at x = 1
C) local maximum 26 at x = -1, local minimum 17 at x = 2
D) local maximum 17 at x = -1, local minimum 26 at x = 2
E) no local extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
47
Find all local extreme values of the function f(x) = 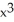 - 6
- 6 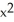 + 12x - 5 and their locations.
+ 12x - 5 and their locations.
A) local maximum 3 at x = 2, local minimum -61 at x = -2
B) local maximum -61 at x = -2, local minimum 3 at x = 2
C) local maximum 3 at x = -2, local minimum -61 at x = 2
D) local maximum -61 at x = 2, local minimum 3 at x = -2
E) no local extrema
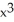 - 6
- 6 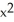 + 12x - 5 and their locations.
+ 12x - 5 and their locations.A) local maximum 3 at x = 2, local minimum -61 at x = -2
B) local maximum -61 at x = -2, local minimum 3 at x = 2
C) local maximum 3 at x = -2, local minimum -61 at x = 2
D) local maximum -61 at x = 2, local minimum 3 at x = -2
E) no local extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
48
Find any extreme values of the function f(x) = 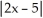 - 7 and their locations.
- 7 and their locations.
A) local (and absolute) minimum -7 at x = 5/2, no local maxima
B) local (and absolute) maximum -7 at x = 5/2, no local minima
C) local (and absolute) minimum -7 at x = 5/2, local maximum -2 at x = 0
D) local (and absolute) maximum -7 at x = 5/2, local minimum -2 at x = 0
E) no absolute or local extrema
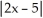 - 7 and their locations.
- 7 and their locations.A) local (and absolute) minimum -7 at x = 5/2, no local maxima
B) local (and absolute) maximum -7 at x = 5/2, no local minima
C) local (and absolute) minimum -7 at x = 5/2, local maximum -2 at x = 0
D) local (and absolute) maximum -7 at x = 5/2, local minimum -2 at x = 0
E) no absolute or local extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
49
At what values of t does the function g(t) = 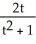 have extreme values?
have extreme values?
A) absolute maximum at t = 1, absolute minimum at t = -1, no other local extrema
B) absolute maximum at t = 1, absolute minimum at t = 0, no other local extrema
C) absolute maximum at t = 2, absolute minimum at t = 0, no other local extrema
D) absolute maximum at t = 2, absolute minimum at t = -2, no other local extrema
E) no absolute or local extrema
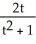 have extreme values?
have extreme values?A) absolute maximum at t = 1, absolute minimum at t = -1, no other local extrema
B) absolute maximum at t = 1, absolute minimum at t = 0, no other local extrema
C) absolute maximum at t = 2, absolute minimum at t = 0, no other local extrema
D) absolute maximum at t = 2, absolute minimum at t = -2, no other local extrema
E) no absolute or local extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
50
Find any extreme values of the function f(x) = x 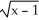 .
.
A) absolute minimum 0 at x = 1, no maxima
B) absolute minimum 0 at x = 0, local maximum 2 at x = 2
C) absolute minimum 0 at x = 0, no local maxima
D) absolute minimum 0 at x = 1, local maximum 2 at x = 2
E) no absolute or local extrema
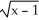 .
.A) absolute minimum 0 at x = 1, no maxima
B) absolute minimum 0 at x = 0, local maximum 2 at x = 2
C) absolute minimum 0 at x = 0, no local maxima
D) absolute minimum 0 at x = 1, local maximum 2 at x = 2
E) no absolute or local extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
51
Find the absolute maximum and absolute minimum values of the function f(x) = 2 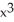 - 3
- 3 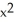 , -2 x 2.
, -2 x 2.
A) maximum 4, minimum -28
B) maximum 2, minimum -26
C) maximum 3, minimum -29
D) maximum 4, minimum -12
E) no absolute extrema
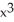 - 3
- 3 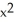 , -2 x 2.
, -2 x 2.A) maximum 4, minimum -28
B) maximum 2, minimum -26
C) maximum 3, minimum -29
D) maximum 4, minimum -12
E) no absolute extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
52
Find the absolute maximum and absolute minimum values of the function f(x) = 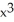 -
- 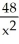 , -4 x -1.
, -4 x -1.
A) maximum -20, minimum -67
B) maximum -20, minimum -49
C) maximum -49, minimum -67
D) maximum -4, minimum -67
E) no absolute extrema
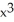 -
- 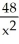 , -4 x -1.
, -4 x -1.A) maximum -20, minimum -67
B) maximum -20, minimum -49
C) maximum -49, minimum -67
D) maximum -4, minimum -67
E) no absolute extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
53
Find the absolute maximum and absolute minimum values of the function f(x) = 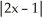 - 1, 0 x 2.
- 1, 0 x 2.
A) maximum 2, minimum -1
B) maximum 2, minimum 0
C) maximum 2, minimum -2
D) maximum 3, minimum -2
E) no absolute extrema
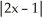 - 1, 0 x 2.
- 1, 0 x 2.A) maximum 2, minimum -1
B) maximum 2, minimum 0
C) maximum 2, minimum -2
D) maximum 3, minimum -2
E) no absolute extrema

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
54
Find the minimum values of the function f(x) = 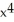 -
- 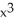 .
.
A) -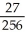
B) 0
C) -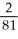
D) -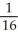
E) no local or absolute minima
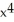 -
- 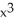 .
.A) -
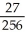
B) 0
C) -
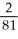
D) -
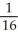
E) no local or absolute minima

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
55
For what value of k will f(x) = 2x - 3k 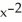 , have a local minimum at x = 1?
, have a local minimum at x = 1?
A) k =
B) k = -
C) k = 3
D) k = 0
E) k = -3
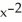 , have a local minimum at x = 1?
, have a local minimum at x = 1?A) k =

B) k = -

C) k = 3
D) k = 0
E) k = -3

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
56
Find the extreme values of f(x) = x - 2 sin x on [0, ].
A) maximum , minimum![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_95b3_a0f8_1f68d9a5de85_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_95b4_a0f8_978fce8d1a7a_TB9661_11.jpg)
B) maximum![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc5_a0f8_93b52ab178f3_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc6_a0f8_7f91f56b9714_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc7_a0f8_e1aee6a71ce7_TB9661_11.jpg)
C) maximum![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc8_a0f8_59edeb49c741_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc9_a0f8_6fe640ba2e5a_TB9661_11.jpg) - 2
- 2
D) maximum![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcca_a0f8_b5fad35f51b6_TB9661_11.jpg) +
+ ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bccb_a0f8_3f652138e14d_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bccc_a0f8_99a4eb937f9c_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bccd_a0f8_39457adb1e08_TB9661_11.jpg)
E) no extreme values
A) maximum , minimum
![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_95b3_a0f8_1f68d9a5de85_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_95b4_a0f8_978fce8d1a7a_TB9661_11.jpg)
B) maximum
![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc5_a0f8_93b52ab178f3_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc6_a0f8_7f91f56b9714_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc7_a0f8_e1aee6a71ce7_TB9661_11.jpg)
C) maximum
![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc8_a0f8_59edeb49c741_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcc9_a0f8_6fe640ba2e5a_TB9661_11.jpg) - 2
- 2D) maximum
![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bcca_a0f8_b5fad35f51b6_TB9661_11.jpg) +
+ ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bccb_a0f8_3f652138e14d_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bccc_a0f8_99a4eb937f9c_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x - 2 sin x on [0, \pi ].</strong> A) maximum \pi , minimum - B) maximum , minimum - C) maximum , minimum - 2 D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7825_bccd_a0f8_39457adb1e08_TB9661_11.jpg)
E) no extreme values

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
57
Find the extreme values of f(x) = x + ![Find the extreme values of f(x) = x + cos x on [0, π].](https://storage.examlex.com/TB9661/11ee77e1_7825_e3de_a0f8_73b9b2a0874a_TB9661_11.jpg) cos x on [0, π].
cos x on [0, π].
![Find the extreme values of f(x) = x + cos x on [0, π].](https://storage.examlex.com/TB9661/11ee77e1_7825_e3de_a0f8_73b9b2a0874a_TB9661_11.jpg) cos x on [0, π].
cos x on [0, π].
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
58
Find the extreme values of f(x) = x + ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_0af3_a0f8_d9ed2a6da1c9_TB9661_11.jpg) cos x on [0, ].
cos x on [0, ].
A) maximum![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_0af4_a0f8_0304d59cf66f_TB9661_11.jpg) + 1, minimum
+ 1, minimum ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_0af5_a0f8_d9cd1c93a06d_TB9661_11.jpg) - 1
- 1
B) maximum![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3206_a0f8_b311bc57c47e_TB9661_11.jpg) , minimum -
, minimum - ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3207_a0f8_1b2862e01326_TB9661_11.jpg)
C) maximum -![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3208_a0f8_fbbe35315f6f_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3209_a0f8_a3dcfb9de491_TB9661_11.jpg)
D) maximum![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320a_a0f8_976233538991_TB9661_11.jpg) +
+ ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320b_a0f8_8ffea83641ae_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320c_a0f8_19dc95855905_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320d_a0f8_fdf5c1736181_TB9661_11.jpg)
E) no extreme values
![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_0af3_a0f8_d9ed2a6da1c9_TB9661_11.jpg) cos x on [0, ].
cos x on [0, ].A) maximum
![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_0af4_a0f8_0304d59cf66f_TB9661_11.jpg) + 1, minimum
+ 1, minimum ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_0af5_a0f8_d9cd1c93a06d_TB9661_11.jpg) - 1
- 1B) maximum
![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3206_a0f8_b311bc57c47e_TB9661_11.jpg) , minimum -
, minimum - ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3207_a0f8_1b2862e01326_TB9661_11.jpg)
C) maximum -
![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3208_a0f8_fbbe35315f6f_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_3209_a0f8_a3dcfb9de491_TB9661_11.jpg)
D) maximum
![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320a_a0f8_976233538991_TB9661_11.jpg) +
+ ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320b_a0f8_8ffea83641ae_TB9661_11.jpg) , minimum
, minimum ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320c_a0f8_19dc95855905_TB9661_11.jpg) -
- ![<strong>Find the extreme values of f(x) = x + cos x on [0, \pi ].</strong> A) maximum + 1, minimum - 1 B) maximum , minimum \pi - C) maximum \pi - , minimum D) maximum + , minimum - E) no extreme values](https://storage.examlex.com/TB9661/11ee77e1_7826_320d_a0f8_fdf5c1736181_TB9661_11.jpg)
E) no extreme values

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
59
The function f(x) = 4 + k 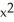 -
- 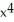 has a maximum value at x = 2. Find k.
has a maximum value at x = 2. Find k.
A) k = 8
B) k = -8
C) k = 4
D) k = -4
E) k = 0
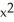 -
- 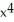 has a maximum value at x = 2. Find k.
has a maximum value at x = 2. Find k.A) k = 8
B) k = -8
C) k = 4
D) k = -4
E) k = 0

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
60
Find the absolute maximum and minimum values (if any) of f(x) = 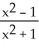 .
.
A) minimum -1, maximum 1
B) minimum -1, no maximum
C) no minimum, maximum 1
D) minimum -1, maximum 0
E) no absolute maximum or minimum
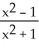 .
.A) minimum -1, maximum 1
B) minimum -1, no maximum
C) no minimum, maximum 1
D) minimum -1, maximum 0
E) no absolute maximum or minimum

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
61
Find the maximum value of the function f(x) = 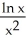 .
.
A)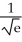
B)
C) 1
D)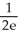
E) no maximum value
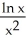 .
.A)
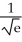
B)

C) 1
D)
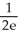
E) no maximum value

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
62
Let g(x) = 3(x - 1)2/3 - x. Which of the following statements is true?
A) g has a local maximum at (1, -1) and a local minimum at (9, 3).
B) g is increasing on the interval (- , 9).
C) g has a local maximum at (9, 3) and a local minimum at (1, -1).
D) g is decreasing on the interval (1, 9).
E) g is decreasing on the interval (- , 9).
A) g has a local maximum at (1, -1) and a local minimum at (9, 3).
B) g is increasing on the interval (- , 9).
C) g has a local maximum at (9, 3) and a local minimum at (1, -1).
D) g is decreasing on the interval (1, 9).
E) g is decreasing on the interval (- , 9).

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
63
Find and classify all the local extrema of the function f(x) = x - sin2x.
A) local minima at x = k +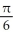 and local maxima at x = k -
and local maxima at x = k - 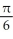 , where k is an integer
, where k is an integer
B) local maxima at x = k +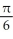 and local minima at x = k -
and local minima at x = k - 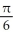 , where k is an integer
, where k is an integer
C) local maxima at x = k +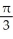 and local minima at x = k -
and local minima at x = k - 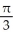 , where k is an integer
, where k is an integer
D) local minima at x = k +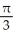 and local maxima at x = k -
and local maxima at x = k - 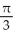 , where k is an integer
, where k is an integer
E) local minima at x = 2k +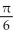 and local maxima at x = 2k -
and local maxima at x = 2k - 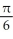 , where k is an integer
, where k is an integer
A) local minima at x = k +
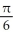 and local maxima at x = k -
and local maxima at x = k - 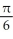 , where k is an integer
, where k is an integerB) local maxima at x = k +
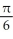 and local minima at x = k -
and local minima at x = k - 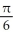 , where k is an integer
, where k is an integerC) local maxima at x = k +
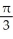 and local minima at x = k -
and local minima at x = k - 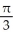 , where k is an integer
, where k is an integerD) local minima at x = k +
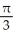 and local maxima at x = k -
and local maxima at x = k - 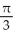 , where k is an integer
, where k is an integerE) local minima at x = 2k +
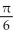 and local maxima at x = 2k -
and local maxima at x = 2k - 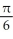 , where k is an integer
, where k is an integer
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
64
Determine the concavity of f(x) = 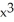 - 24
- 24 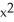 + 6x + 18 and identify any points of inflection.
+ 6x + 18 and identify any points of inflection.
A) concave downwards on (- , 8), upwards on (8, ); inflection at x = 8
B) concave downwards on (- , -8), upwards on (-8, ); inflection at x = -8
C) concave upwards on (- , 8), downwards on (8, ); inflection at x = 8
D) concave upwards on (- , -8), downwards on (-8, ); inflection at x = -8
E) concave upwards on (- , ); no inflection points
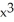 - 24
- 24 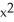 + 6x + 18 and identify any points of inflection.
+ 6x + 18 and identify any points of inflection.A) concave downwards on (- , 8), upwards on (8, ); inflection at x = 8
B) concave downwards on (- , -8), upwards on (-8, ); inflection at x = -8
C) concave upwards on (- , 8), downwards on (8, ); inflection at x = 8
D) concave upwards on (- , -8), downwards on (-8, ); inflection at x = -8
E) concave upwards on (- , ); no inflection points

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
65
Determine the concavity of f(x) = cos x + sin x on [0, 2 ] and identify any points of inflection.
A) concave down on [0, 3 /4)![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11.jpg) (7 /4, 2 ], concave on (3 /4, 7 /4); inflection points at x = 3 /4 and
(7 /4, 2 ], concave on (3 /4, 7 /4); inflection points at x = 3 /4 and ![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_4391_a0f8_2b34495d0ba4_TB9661_11.jpg)
B) concave up on [0, 3 /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (7 /4, 2 ], concave down on (3 /4, 7 /4); inflection points at x = 3 /4 and![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_4392_a0f8_c913310a9fb4_TB9661_11.jpg)
C) concave down on [0, /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (5 /4, 2 ], concave up on ( /4, 5 /4); inflection points at x = /4 and![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_4393_a0f8_6530a91cfcbe_TB9661_11.jpg)
D) concave up on [0, /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (5 /4, 2 ], concave down on ( /4, 5 /4); inflection points at x = /4 and![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_6aa4_a0f8_19008de1a10d_TB9661_11.jpg)
E) concave down on (0, 3 /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (7 /4, 2 ), concave up on (3 /4, 7 /4); inflection points at x = 3 /4 and![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_6aa5_a0f8_a1b06871ebbd_TB9661_11.jpg)
A) concave down on [0, 3 /4)
![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11.jpg) (7 /4, 2 ], concave on (3 /4, 7 /4); inflection points at x = 3 /4 and
(7 /4, 2 ], concave on (3 /4, 7 /4); inflection points at x = 3 /4 and ![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_4391_a0f8_2b34495d0ba4_TB9661_11.jpg)
B) concave up on [0, 3 /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (7 /4, 2 ], concave down on (3 /4, 7 /4); inflection points at x = 3 /4 and
![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_4392_a0f8_c913310a9fb4_TB9661_11.jpg)
C) concave down on [0, /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (5 /4, 2 ], concave up on ( /4, 5 /4); inflection points at x = /4 and
![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_4393_a0f8_6530a91cfcbe_TB9661_11.jpg)
D) concave up on [0, /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (5 /4, 2 ], concave down on ( /4, 5 /4); inflection points at x = /4 and
![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_6aa4_a0f8_19008de1a10d_TB9661_11.jpg)
E) concave down on (0, 3 /4) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (7 /4, 2 ), concave up on (3 /4, 7 /4); inflection points at x = 3 /4 and
![<strong>Determine the concavity of f(x) = cos x + sin x on [0, 2 \pi ] and identify any points of inflection.</strong> A) concave down on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and B) concave up on [0, 3 \pi /4) (7 \pi /4, 2 \pi ], concave down on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and C) concave down on [0, \pi /4) (5 \pi /4, 2 \pi ], concave up on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and D) concave up on [0, \pi /4) (5 \pi /4, 2 \pi ], concave down on ( \pi /4, 5 \pi /4); inflection points at x = \pi /4 and E) concave down on (0, 3 \pi /4) (7 \pi /4, 2 \pi ), concave up on (3 \pi /4, 7 \pi /4); inflection points at x = 3 \pi /4 and](https://storage.examlex.com/TB9661/11ee77e1_7827_6aa5_a0f8_a1b06871ebbd_TB9661_11.jpg)

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
66
Find all inflection points of the graph of f(x) = 3 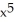 - 5
- 5 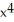 + 13x.
+ 13x.
A) (0, 0) and (1, 11)
B) (0, 0) only
C) (1, 11) only
D) (-1, -21) and (1, 11)
E) (-1, -21), (0, 0), and (1, 11)
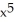 - 5
- 5 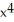 + 13x.
+ 13x.A) (0, 0) and (1, 11)
B) (0, 0) only
C) (1, 11) only
D) (-1, -21) and (1, 11)
E) (-1, -21), (0, 0), and (1, 11)

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
67
Let f(x) = 18 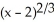 + 9
+ 9 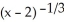 . The first and the second order derivatives of f are given by
. The first and the second order derivatives of f are given by  (x) =
(x) = 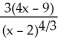 and
and 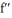 (x) =
(x) = 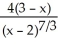 , respectively. Determine:(a) intervals of concavity.(b) the x and y coordinates of the inflection points.
, respectively. Determine:(a) intervals of concavity.(b) the x and y coordinates of the inflection points.
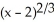 + 9
+ 9 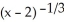 . The first and the second order derivatives of f are given by
. The first and the second order derivatives of f are given by  (x) =
(x) = 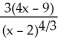 and
and  (x) =
(x) = 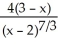 , respectively. Determine:(a) intervals of concavity.(b) the x and y coordinates of the inflection points.
, respectively. Determine:(a) intervals of concavity.(b) the x and y coordinates of the inflection points.
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
68
Find any extreme values and points of inflection of the function f(x) = x4 - 4 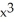 + 10.
+ 10.
A) absolute minimum -17 at x = 3; local maximum 10 at x = 0; inflection at x = 2
B) absolute minimum -17 at x = 3; inflections at x = 0 and x = 2
C) absolute maximum 10 at x = 0; inflections at x = 2 and x = 3
D) absolute maximum -17 at x = 3; inflections at x = 0 and x = 2
E) absolute maximum -17 at x = 3; local minimum 10 at x = 0; inflection at x = 2
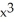 + 10.
+ 10.A) absolute minimum -17 at x = 3; local maximum 10 at x = 0; inflection at x = 2
B) absolute minimum -17 at x = 3; inflections at x = 0 and x = 2
C) absolute maximum 10 at x = 0; inflections at x = 2 and x = 3
D) absolute maximum -17 at x = 3; inflections at x = 0 and x = 2
E) absolute maximum -17 at x = 3; local minimum 10 at x = 0; inflection at x = 2

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
69
Using the second derivative test, classify the critical points of the function f(t) = t3 - t2 - t + 2 and locate any points of inflection.
A) local max at t = -1/3, local min at t = 1, inflection at t = 1/3
B) local min at t = -1/3, local max at t = 1, inflection at t = 1/3
C) local max at t = 1/3, local min at t = -1, inflection at t = -1/3
D) local min at t = 1/3, local max at t = -1, inflection at t = -1/3
E) none of the above
A) local max at t = -1/3, local min at t = 1, inflection at t = 1/3
B) local min at t = -1/3, local max at t = 1, inflection at t = 1/3
C) local max at t = 1/3, local min at t = -1, inflection at t = -1/3
D) local min at t = 1/3, local max at t = -1, inflection at t = -1/3
E) none of the above

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
70
Let g be a polynomial function such that 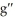 (x) = (x + 2)(
(x) = (x + 2)( 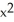 - 10x -24). Find the x-coordinate of all inflection points of the graph of g.
- 10x -24). Find the x-coordinate of all inflection points of the graph of g.
A) only -2
B) -2 and 12
C) - 2 , 4, and 6
D) only 12
E) -2, - 4, and -6
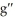 (x) = (x + 2)(
(x) = (x + 2)( 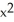 - 10x -24). Find the x-coordinate of all inflection points of the graph of g.
- 10x -24). Find the x-coordinate of all inflection points of the graph of g.A) only -2
B) -2 and 12
C) - 2 , 4, and 6
D) only 12
E) -2, - 4, and -6

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
71
Find the inflection points of the graph of f(x) = 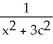 where c is a nonzero constant.
where c is a nonzero constant.
A)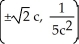
B)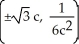
C)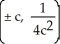
D)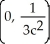
E) There are no inflection points.
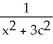 where c is a nonzero constant.
where c is a nonzero constant.A)
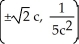
B)
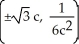
C)
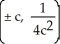
D)
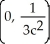
E) There are no inflection points.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
72
The function f(x) = 3x5 + Ax4 + Bx3 has inflection points at x = 0, x = -1, and x = 1. Find the values of the constants A and B.
A) A = 0, B = -10
B) A = 0, B = 10
C) A has any value, B = -10
D) A has any value, B = 10
E) A = 10, B = 0
A) A = 0, B = -10
B) A = 0, B = 10
C) A has any value, B = -10
D) A has any value, B = 10
E) A = 10, B = 0

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
73
Determine the concavity of f(x) = cos x + sin x on [0, 2π] and identify any points of inflection.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
74
At what value(s) of x does the graph of f(x) = x 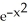 have inflections?
have inflections?
A) ±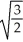
B) 0 and ±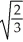
C) ±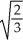
D) 0 and ±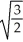
E) 0
 have inflections?
have inflections?A) ±
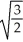
B) 0 and ±
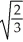
C) ±
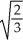
D) 0 and ±
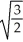
E) 0

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
75
Which of the following statements best describes the graph of the function f(x) = 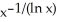 ?
?
A) The graph is concave up on (0, ).
B) The graph is concave down on (0, ).
C) The graph is concave up on (0,e) and concave down on (e, ).
D) The graph is a straight line.
E) The graph is concave down on (0,e) and concave up on (e, ).
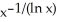 ?
?A) The graph is concave up on (0, ).
B) The graph is concave down on (0, ).
C) The graph is concave up on (0,e) and concave down on (e, ).
D) The graph is a straight line.
E) The graph is concave down on (0,e) and concave up on (e, ).

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
76
Determine the concavity and inflections of f(x) = 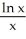 .
.
A)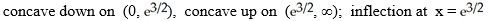
B)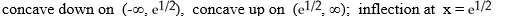
C)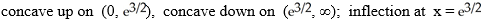
D)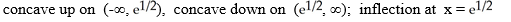
E) concave up on (0, )
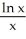 .
.A)
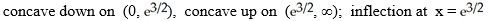
B)
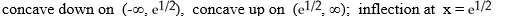
C)
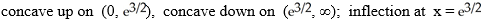
D)
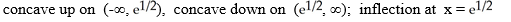
E) concave up on (0, )

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
77
Let P(x) be a polynomial in x, let k be a positive integer, and let 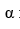 be a number such that
be a number such that 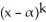 is a factor of
is a factor of 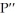 (x) but
(x) but 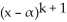 is not a factor of
is not a factor of 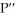 (x). For what values of k is it possible that P(x) has a local maximum or minimum value at x = 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11?
(x). For what values of k is it possible that P(x) has a local maximum or minimum value at x = 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11?
A) even values of k
B) k = 1 only
C) k = 2 only
D) odd values of k
E) k = 0 only
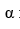 be a number such that
be a number such that 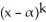 is a factor of
is a factor of  (x) but
(x) but 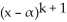 is not a factor of
is not a factor of  (x). For what values of k is it possible that P(x) has a local maximum or minimum value at x = 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11?
(x). For what values of k is it possible that P(x) has a local maximum or minimum value at x = 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11?A) even values of k
B) k = 1 only
C) k = 2 only
D) odd values of k
E) k = 0 only

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
78
What are the asymptotes of the graph of y = 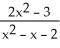 ?
?
A) horizontal asymptote at y = 2, vertical asymptotes at x = -1 and x = 2
B) horizontal asymptote at y = 2, vertical asymptotes at x = 1 and x = -2
C) horizontal asymptote at y =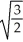 , vertical asymptotes at x = 1 and x = 2
, vertical asymptotes at x = 1 and x = 2
D) oblique asymptote at y = -x - 2, vertical asymptotes at x = -1 and x = 2
E) oblique asymptote at y = x - 2, vertical asymptotes at x = -1 and x = 2
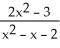 ?
?A) horizontal asymptote at y = 2, vertical asymptotes at x = -1 and x = 2
B) horizontal asymptote at y = 2, vertical asymptotes at x = 1 and x = -2
C) horizontal asymptote at y =
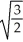 , vertical asymptotes at x = 1 and x = 2
, vertical asymptotes at x = 1 and x = 2D) oblique asymptote at y = -x - 2, vertical asymptotes at x = -1 and x = 2
E) oblique asymptote at y = x - 2, vertical asymptotes at x = -1 and x = 2

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
79
Find the equations of all horizontal asymptotes of f(x) = 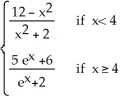
A) y = -1 and y = 5
B) y = -1 and y = 1
C) y = 3
D) y = -1 and y = 3
E) y = 1
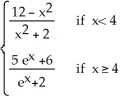
A) y = -1 and y = 5
B) y = -1 and y = 1
C) y = 3
D) y = -1 and y = 3
E) y = 1

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
80
Find the equations of the vertical asymptotes of f(x) = 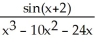
A) x = 0, x = 12, and x = -2
B) x = 0, x = 6, and x = 4
C) x = 0 and x = 12
D) x = 12 and x = -2
E) x = 0, x = -8, and x = -3
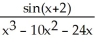
A) x = 0, x = 12, and x = -2
B) x = 0, x = 6, and x = 4
C) x = 0 and x = 12
D) x = 12 and x = -2
E) x = 0, x = -8, and x = -3

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck


