Exam 5: More Applications of Differentiation
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
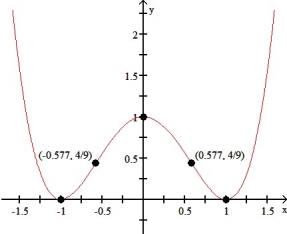
Find the local extrema and inflection points of the function f(x) = 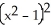 and sketch its graph.
and sketch its graph.
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
Local max at (0, 1), local min at (±1, 0), inflections at (±1/ 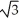 , 4/9)
, 4/9)
At what value(s) of x does the graph of f(x) = x 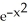 have inflections?
have inflections?
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
D
Using the second derivative test, classify the critical points of the function f(t) = t3 - t2 - t + 2 and locate any points of inflection.
Free
(Multiple Choice)
4.9/5  (28)
(28)
Correct Answer:
A
A function f(x) satisfies the following conditions:
f(1) = 0, f(n) (1) = n for n = 1, 2, and 3,
3x ≤ f(4) (x) ≤ 9x provided x ≥ 1.
(a) What is the Taylor polynomial p3 (x) of degree 3 for f(x) about x = 1?
(b) What is the approximate value for f(3/2) supplied by (x)?
(c) Based on the bounds for f(4) (x) given above, what is the smallest interval that you can be sure
contains the value f(3/2)?
(d) Based on your answer to (c), what is the best approximation you can give for f(3/2)?
(Essay)
4.8/5  (33)
(33)
A plane flying horizontally at an altitude of 1 kilometre and a speed of 500 kilometres per hour passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing at the instant when the plane is 2 kilometres away from the station.
(Multiple Choice)
4.9/5  (31)
(31)
At what values of t does the function g(t) = 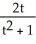 have extreme values?
have extreme values?
(Multiple Choice)
4.8/5  (43)
(43)
Find a suitable linearization for sin(x°) useful near x = 60°.
(Multiple Choice)
4.9/5  (30)
(30)
Let f(x) = 18 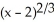 + 9
+ 9 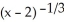 . The first and the second order derivatives of f are given by
. The first and the second order derivatives of f are given by  (x) =
(x) = 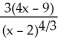 and
and 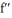 (x) =
(x) = 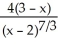 , respectively. Determine:(a) intervals of concavity.(b) the x and y coordinates of the inflection points.
, respectively. Determine:(a) intervals of concavity.(b) the x and y coordinates of the inflection points.
(Essay)
4.9/5  (37)
(37)
For what value of k will f(x) = 2x - 3k 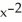 , have a local minimum at x = 1?
, have a local minimum at x = 1?
(Multiple Choice)
4.9/5  (37)
(37)
A hemispherical bowl of radius 10 inches is filled with water to a depth of x inches. The volume V of water in the bowl (in cubic centimetres) is given by the formulaV = 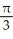 (30
(30 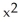 -
- 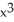 ). Suppose that you measure the depth of water in the bowl to be 5 cm with a maximum possible measured error of 0.5 cm. Estimate the maximum error in the calculated volume of water in the bowl using a linear approximation.
). Suppose that you measure the depth of water in the bowl to be 5 cm with a maximum possible measured error of 0.5 cm. Estimate the maximum error in the calculated volume of water in the bowl using a linear approximation.
(Multiple Choice)
4.8/5  (41)
(41)
A closed rectangular container with a square base is to have a volume of 12 cubic metres. The material for the top and bottom of the container will cost $6 per square metre and the material for the sides will cost $4 per square metre. Let x be the length of a side of the base (in metres) and C(x) be the total cost of the container (in dollars). Determine
(a) the total cost C(x).
(b) the dimensions of the most economical box.
(Essay)
4.7/5  (38)
(38)
Water is leaking out of an inverted conical cup at a rate of 2 cubic centimetres per second. The radius of the cone is six centimetres and the height is 10 centimetres. Find the rate at which the water depth is changing at time t when the depth of the water is 3 centimetres.
(Multiple Choice)
4.7/5  (32)
(32)
Find the solutions of the equation cos x - x4 = 0 to 4 decimal places using Newton's Method.
(Multiple Choice)
4.9/5  (34)
(34)
If the linear approximation of f(x) = 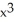 at x = -1 is used to estimate the value of
at x = -1 is used to estimate the value of 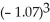 , then the estimated value is the exact value.
, then the estimated value is the exact value.
(True/False)
4.7/5  (32)
(32)
Find the smallest possible area of a triangle formed by the coordinate axes and a line tangent to the ellipse 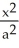 +
+ 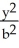 = 1, where a > 0 and b > 0.
= 1, where a > 0 and b > 0.
(Multiple Choice)
4.8/5  (46)
(46)
Find the best linear approximation to the function p(x) = -x3 + 3x at the point (2, -2).
(Multiple Choice)
4.9/5  (31)
(31)
For what values of the nonnegative constant c is the minimum distance from the point(0,c) to the parabola y = x2 equal to c?
(Multiple Choice)
4.9/5  (41)
(41)
Find the absolute maximum and minimum values (if any) of f(x) = 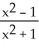 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Showing 1 - 20 of 130
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)