Deck 37: Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/60
Play
Full screen (f)
Deck 37: Infinite Series
1
Use the ratio test to determine if the following series converges or diverges:
converges
2
Use the partial sum test to determine if the series converges: the geometric series:
converges
3
Use the ratio test to determine if the series converges:
diverges
4
Use the ratio test to determine if the series converges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
5
Use the ratio test to determine if the following series converges or diverges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
6
Use the partial sum test to determine if the series converges of diverges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
7
Use the limit test to determine if the series converges of diverges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
8
Use the limit test to determine if the following series converges or diverges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
9
Use the partial sum test to determine if the series converges or diverges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
10
Use the ratio test to determine if the series converges of diverges:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
11
Compute the following number, to three decimal places, using three terms of the appropriate Maclaurin's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
12
Use the ratio test to find the interval of convergence of the following power series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
13
Use the ratio test to find the interval of convergence of the power series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
14
Compute the number to three decimal places using three terms of the appropriate Maclaurin series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
15
Find the first four terms of the Maclaurin series for the function:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
16
Find the first four terms of the Maclaurin series for the function:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
17
Find the first four terms of the Maclaurin series for the function:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
18
Use the ratio test to find the interval of convergence of the power series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
19
Compute the following number, to three decimal places, using three terms of the appropriate Maclaurin's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
20
Compute the value of the following expression, to three decimal places, using three terms of the appropriate Taylor's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
21
Compute the value of the following expression, to three decimal places, using three terms of the appropriate Taylor's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
22
Compute the value of , to three decimal places, using three terms of the Taylor's series expanded about .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
23
Compute the value of the following expression, to three decimal places, using three terms of the appropriate Taylor's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
24
Compute the value of the following expression, to three decimal places, using three terms of the appropriate Taylor's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
25
Compute the value of the following expression, to three decimal places, using three terms of the appropriate Taylor's series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
26
Compute the value of , to three decimal places, using three terms of the Taylor's series expanded about .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
27
Use the series for to find the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
28
Use the series for to find the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
29
Add the appropriate series to obtain the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
30
Multiply the appropriate series to obtain the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
31
Find the series for by differentiating and multiplying by the appropriate factor.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
32
Use the series for to find the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
33
Find the series for by differentiating and multiplying the related series by an appropriate factor.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
34
Add the appropriate series to obtain the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
35
Multiply the appropriate series to obtain the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the integral to three decimal places by integrating the first three terms of the series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate the integral to three decimal places by integrating the first three terms of the series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
38
Add the appropriate series to obtain the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
39
Multiply the appropriate series to obtain the series for .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the integral to three decimal places by integrating the first three terms of the series:

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
41
Write a Fourier series for the function below:
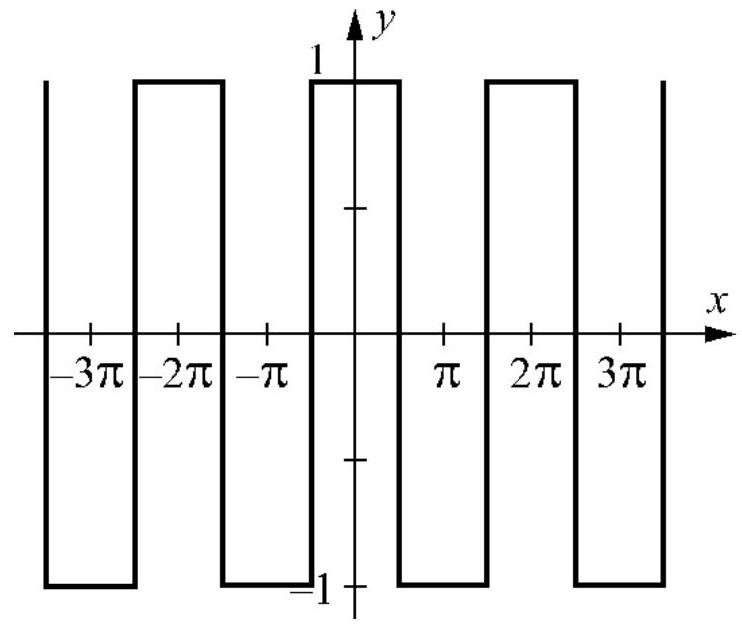


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
42
Write seven terms of the Fourier series given the following coefficients: ,

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
43
Write seven terms of the Fourier series given the following coefficients: ,

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
44
Write a Fourier series for the function below:
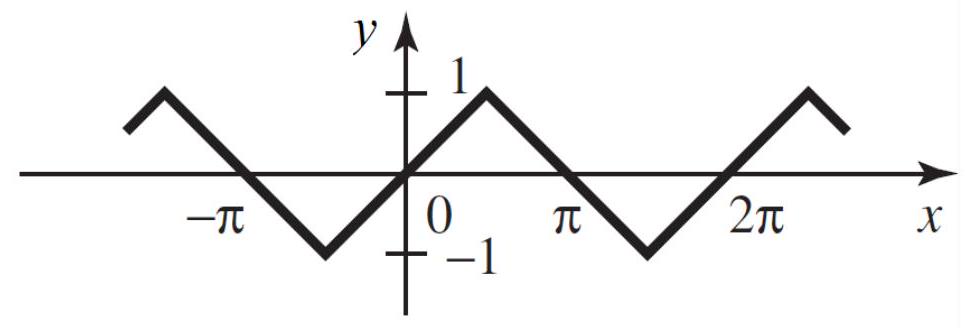
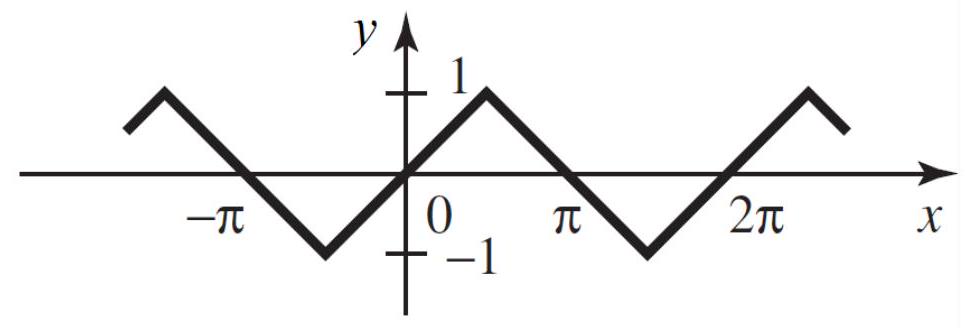

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
45
Write seven terms of the Fourier series given the following coefficients: ,

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
46
Label the function below as odd, even, or neither.
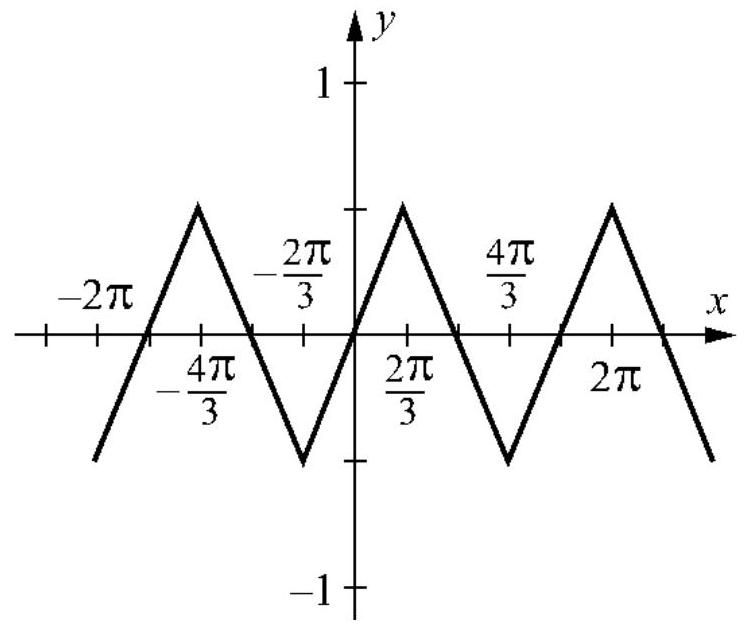


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
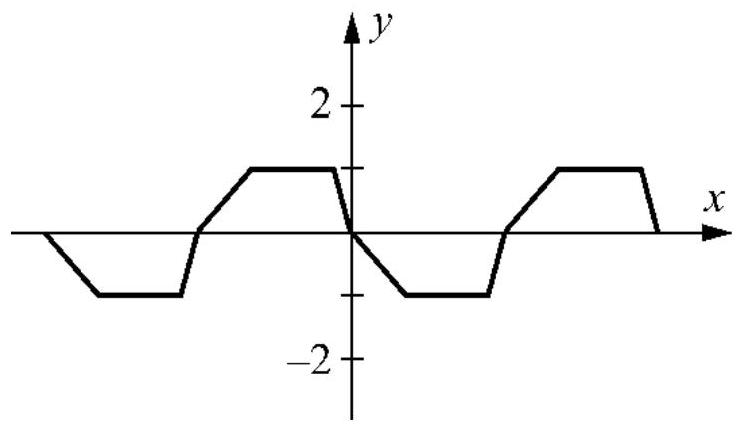
47
Label the function below as odd, even, or neither.


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
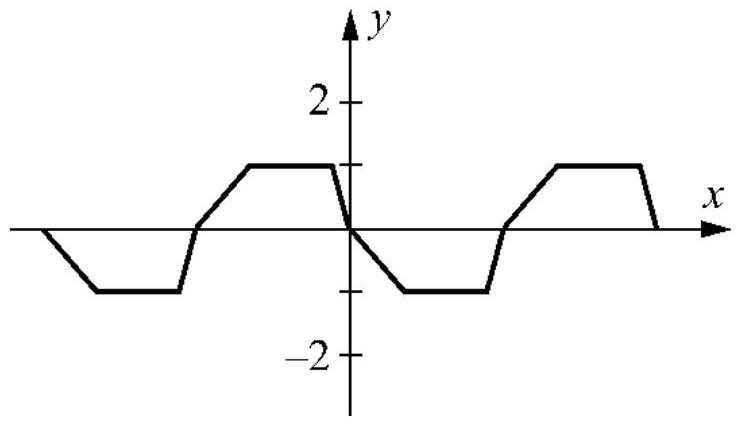
48
Does the function below have half-wave symmetry?


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
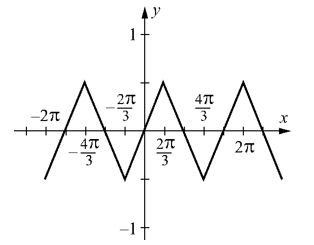
49
Does the function below have half-wave symmetry?


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
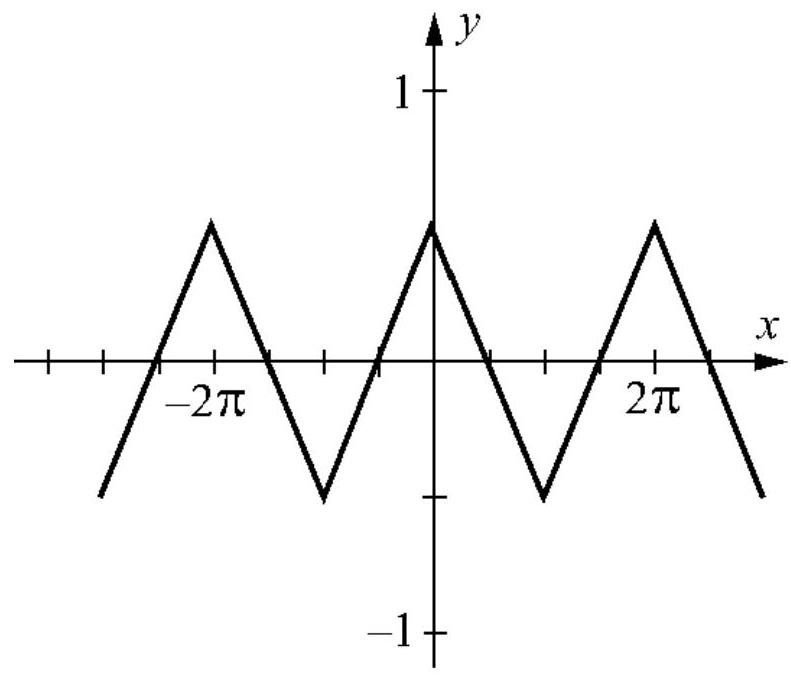
50
Label the function below as odd, even, or neither.


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
51
Label the function below as odd, even, or neither.
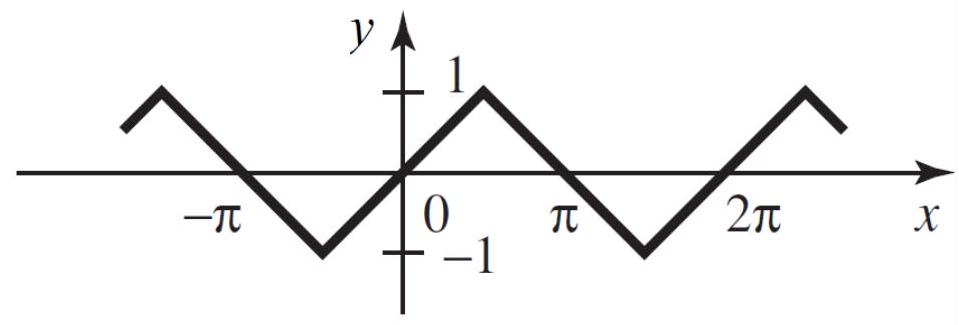
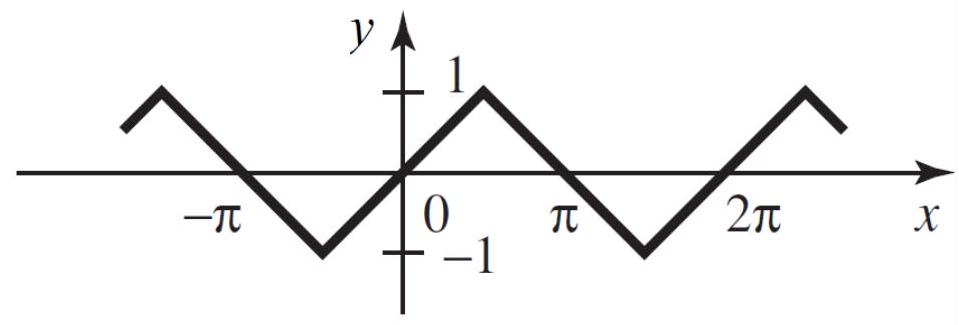

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
52
Verify that the first four terms of the Fourier series for the full wave rectification of the sine function
![Verify that the first four terms of the Fourier series for the full wave rectification of the sine function f(t)=\sin (2 \pi f t){f=1 \text { below are: }} f(t)=\frac{2}{\pi}\left[1-2\left(\frac{1}{3} \cos 2 \pi t+\frac{1}{15} \cos 4 \pi t+\frac{1}{35} \cos 6 \pi t\right)\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a592_87de_576c5eb89a0d_TB10878_00.jpg)
![Verify that the first four terms of the Fourier series for the full wave rectification of the sine function f(t)=\sin (2 \pi f t){f=1 \text { below are: }} f(t)=\frac{2}{\pi}\left[1-2\left(\frac{1}{3} \cos 2 \pi t+\frac{1}{15} \cos 4 \pi t+\frac{1}{35} \cos 6 \pi t\right)\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a592_87de_576c5eb89a0d_TB10878_00.jpg)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
53
Verify that the first four terms of the Fourier series for the half wave Rectification of the sine function
![Verify that the first four terms of the Fourier series for the half wave Rectification of the sine function f(t)=\sin (2 \pi f t) {f=1} \text { below are: } f(t)=\frac{\sin \pi t}{2}+\frac{1}{\pi}\left[1-\frac{2}{3} \cos 4 \pi t+\frac{2}{15} \cos 8 \pi t\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a593_87de_9db3e139ad91_TB10878_00.jpg)
![Verify that the first four terms of the Fourier series for the half wave Rectification of the sine function f(t)=\sin (2 \pi f t) {f=1} \text { below are: } f(t)=\frac{\sin \pi t}{2}+\frac{1}{\pi}\left[1-\frac{2}{3} \cos 4 \pi t+\frac{2}{15} \cos 8 \pi t\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a593_87de_9db3e139ad91_TB10878_00.jpg)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
54
Verify that the first four terms of the Fourier series for the sawtooth function below are:
![Verify that the first four terms of the Fourier series for the sawtooth function below are: f(t)=\frac{1}{2}-\frac{1}{\pi}\left[\sin 2 \pi t+\frac{1}{2} \sin 4 \pi t+\frac{1}{3} \sin 6 \pi t\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a594_87de_75c3f6f24669_TB10878_00.jpg)
![Verify that the first four terms of the Fourier series for the sawtooth function below are: f(t)=\frac{1}{2}-\frac{1}{\pi}\left[\sin 2 \pi t+\frac{1}{2} \sin 4 \pi t+\frac{1}{3} \sin 6 \pi t\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a594_87de_75c3f6f24669_TB10878_00.jpg)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
55
Write a Fourier series for the waveform below:
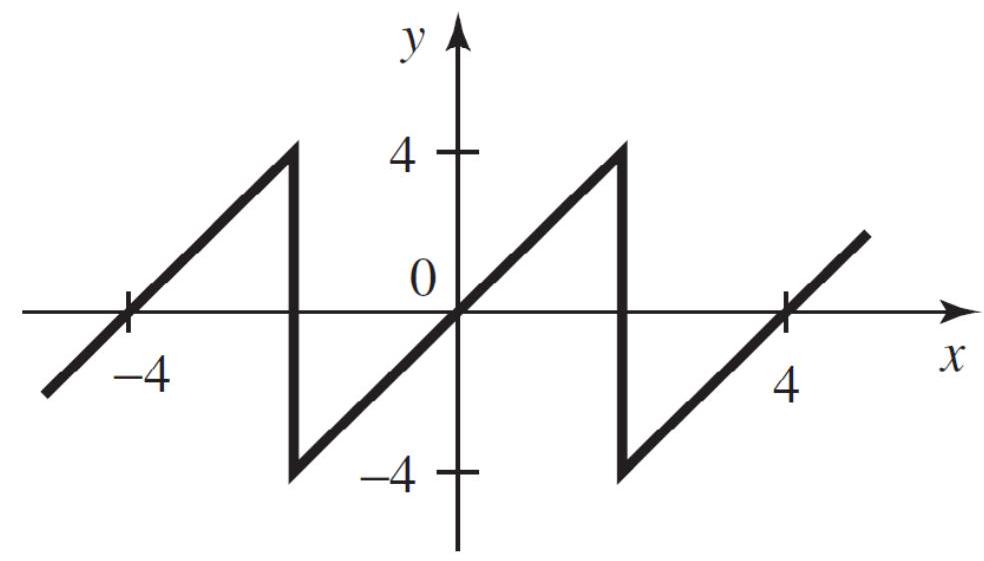


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
56
Find the first six terms of the following waveform. Assume half-wave symmetry.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
57
Find the first four terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
58
Find the first four terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
59
Find the first six terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
60
Find the first six terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck


