Exam 37: Infinite Series
Exam 1: Numerical Computation129 Questions
Exam 2: Introduction to Algebra130 Questions
Exam 3: Simple Equations and Word Problems83 Questions
Exam 4: Functions85 Questions
Exam 5: Graphs64 Questions
Exam 6: Geometry103 Questions
Exam 7: Right Triangles and Vectors88 Questions
Exam 8: Factors and Factoring136 Questions
Exam 9: Fractions and Fractional Equations155 Questions
Exam 10: Systems of Linear Equations75 Questions
Exam 11: Determinants75 Questions
Exam 12: Matrices96 Questions
Exam 13: Exponents and Radicals125 Questions
Exam 14: Quadratic Equations151 Questions
Exam 15: Oblique Triangles and Vectors89 Questions
Exam 16: Radian Measure, Arc Length, and Circular Motion75 Questions
Exam 17: Graphs of the Trigonometric Functions70 Questions
Exam 18: Trigonometric Identities and Equations116 Questions
Exam 19: Ratio, Proportion, and Variation98 Questions
Exam 20: Exponential and Logarithmic Functions140 Questions
Exam 21: Complex Numbers115 Questions
Exam 22: Analytic Geometry129 Questions
Exam 23: Binary, Hexadecimal, Octal, and Bcd Numbers110 Questions
Exam 24: Inequalities and Linear Programming39 Questions
Exam 25: Sequences, Series, and the Binomial Theorem121 Questions
Exam 26: Introduction to Statistics and Probability68 Questions
Exam 27: Derivatives of Algebraic Functions83 Questions
Exam 28: Graphical Applications of the Derivative50 Questions
Exam 29: Applied Applications of the Derivative71 Questions
Exam 30: Integration69 Questions
Exam 31: Applications of the Integral50 Questions
Exam 32: More Applications of the Integral58 Questions
Exam 33: Derivatives of Trigonometric, Logarithmic, and Exponential Functions113 Questions
Exam 34: Methods of Integration89 Questions
Exam 35: Differential Equations103 Questions
Exam 36: Solving Differential Equations by the Laplace Transform and by Numerical Methods56 Questions
Exam 37: Infinite Series60 Questions
Select questions type
Compute the value of , to three decimal places, using three terms of the Taylor's series expanded about .
Free
(Short Answer)
4.8/5  (30)
(30)
Correct Answer:
3.316
Does the function below have half-wave symmetry?
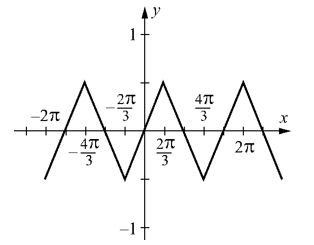
Free
(True/False)
4.9/5  (38)
(38)
Correct Answer:
True
Find the first four terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.
3 6 9 12 16 18 0 3.1 4.5 8.1 15.1 14.4 0
Free
(Essay)
4.8/5  (35)
(35)
Correct Answer:
Find the first four terms of the Maclaurin series for the function:
(Short Answer)
4.9/5  (37)
(37)
Evaluate the integral to three decimal places by integrating the first three terms of the series:
(Short Answer)
4.7/5  (29)
(29)
Use the ratio test to determine if the series converges of diverges:
(Short Answer)
4.8/5  (42)
(42)
Use the ratio test to determine if the following series converges or diverges:
(Short Answer)
4.9/5  (30)
(30)
Compute the value of the following expression, to three decimal places, using three terms of the appropriate Taylor's series:
(Short Answer)
4.8/5  (27)
(27)
Find the first six terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.
2 4 6 8 10 12 14 16 18 0 2.1 4.8 7.5 11.2 10.9 6.8 5.2 2.4 0
(Essay)
4.7/5  (32)
(32)
Find the first four terms of the Maclaurin series for the function:
(Short Answer)
4.7/5  (35)
(35)
Find the first six terms (rounded to three decimal places) of the Fourier series. Assume half-wave symmetry.
2 4 6 8 10 12 14 16 18 0 4 7.5 10 8 6.5 5 4 2 0
(Essay)
4.8/5  (36)
(36)
Find the series for by differentiating and multiplying by the appropriate factor.
(Short Answer)
4.9/5  (37)
(37)
Verify that the first four terms of the Fourier series for the sawtooth function below are:
![Verify that the first four terms of the Fourier series for the sawtooth function below are: f(t)=\frac{1}{2}-\frac{1}{\pi}\left[\sin 2 \pi t+\frac{1}{2} \sin 4 \pi t+\frac{1}{3} \sin 6 \pi t\right]](https://storage.examlex.com/TB10878/11eedbb5_5b9c_a594_87de_75c3f6f24669_TB10878_00.jpg)
(Short Answer)
4.8/5  (30)
(30)
Find the series for by differentiating and multiplying the related series by an appropriate factor.
(Short Answer)
4.9/5  (35)
(35)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)