Deck 6: Systems of Linear Equations and Matrices
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/215
Play
Full screen (f)
Deck 6: Systems of Linear Equations and Matrices
1
Determine whether the given ordered set of numbers is a solution of the system of equations.
-(-6,-2)
-(-6,-2)
True
2
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
-
False
3
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
-
True
4
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
-

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
-

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
-

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system of two equations in two variables.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the system of two equations in two variables.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the system of two equations in two variables.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system of two equations in two variables.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system of two equations in two variables.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system of two equations in two variables.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system of two equations in two variables.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system of two equations in two variables.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system of two equations in two variables.
-
A) No solution
B)
C)
D) for any real number
-
A) No solution
B)
C)
D) for any real number

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
16
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
17
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
18
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
19
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
20
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
21
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
22
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the problem by writing and solving a suitable system of equations.
-Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged for 3 days and 300 miles, while Mary was charged for 5 days and 600 miles. What does Best Rental charge per day and per mile?
A) per day and 25 cents per mile
B) per day and 29 cents per mile
C) per day and 25 cents per mile
D) per day and 24 cents per mile
-Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged for 3 days and 300 miles, while Mary was charged for 5 days and 600 miles. What does Best Rental charge per day and per mile?
A) per day and 25 cents per mile
B) per day and 29 cents per mile
C) per day and 25 cents per mile
D) per day and 24 cents per mile

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem by writing and solving a suitable system of equations.
-A shopkeeper orders 18 pounds of cashews and peanuts. If the amount of cashews he orders is 14 pounds less than the amount of peanuts, how many pounds of peanuts did he order?
A) 4 pounds
B) 9 pounds
C) 2 pounds
D) 16 pounds
-A shopkeeper orders 18 pounds of cashews and peanuts. If the amount of cashews he orders is 14 pounds less than the amount of peanuts, how many pounds of peanuts did he order?
A) 4 pounds
B) 9 pounds
C) 2 pounds
D) 16 pounds

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the problem by writing and solving a suitable system of equations.
-Carole's car averages 13.0 miles per gallon in city driving and 21.0 miles per gallon in highway driving. If she drove a total of 443.0 miles on 23 gallons of gas, how many of the gallons were used for city driving?
A) 23 gallons
B) 7 gallons
C) 18 gallons
D) 5 gallons
-Carole's car averages 13.0 miles per gallon in city driving and 21.0 miles per gallon in highway driving. If she drove a total of 443.0 miles on 23 gallons of gas, how many of the gallons were used for city driving?
A) 23 gallons
B) 7 gallons
C) 18 gallons
D) 5 gallons

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the problem by writing and solving a suitable system of equations.
-If 40 pounds of tomatoes and 20 pounds of bananas cost and 10 pounds of tomatoes and 30 pounds of bananas cost , what is the price per pound of tomatoes and bananas
A) tomatoes: per pound; bananas: per pound
B) tomatoes: per pound; bananas: per pound
C) tomatoes: per pound; bananas: per pound
D) tomatoes: per pound; bananas: per pound
-If 40 pounds of tomatoes and 20 pounds of bananas cost and 10 pounds of tomatoes and 30 pounds of bananas cost , what is the price per pound of tomatoes and bananas
A) tomatoes: per pound; bananas: per pound
B) tomatoes: per pound; bananas: per pound
C) tomatoes: per pound; bananas: per pound
D) tomatoes: per pound; bananas: per pound

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
27
Obtain an equivalent system by performing the stated elementary operation on the system.
-Interchange equations 1 and 3.
A)
B)
C)
D)
-Interchange equations 1 and 3.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
28
Obtain an equivalent system by performing the stated elementary operation on the system.
-Multiply the second equation by -1 .
A) x - 5y + z = 5
-3x + 3y + z = 18
5x + y + 4z = -12
X - 3y + z = -7
B) x - 5y + z = 5
-3x - 3y - z = -18
5x + y + 4z = -12
X - 3y + z = -7
C) x - 5y + z = 5
-3x + 3y + z = -18
5x + y + 4z = -12
X - 3y + z = -7
D) -x + 5y - z = -5
3x - 3y - z = -18
5x + y + 4z = -12
X - 3y + z = -7
-Multiply the second equation by -1 .
A) x - 5y + z = 5
-3x + 3y + z = 18
5x + y + 4z = -12
X - 3y + z = -7
B) x - 5y + z = 5
-3x - 3y - z = -18
5x + y + 4z = -12
X - 3y + z = -7
C) x - 5y + z = 5
-3x + 3y + z = -18
5x + y + 4z = -12
X - 3y + z = -7
D) -x + 5y - z = -5
3x - 3y - z = -18
5x + y + 4z = -12
X - 3y + z = -7

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
29
Obtain an equivalent system by performing the stated elementary operation on the system.
-Multiply the third equation by .
A)
B)
C)
D)
-Multiply the third equation by .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
30
Obtain an equivalent system by performing the stated elementary operation on the system.
-Replace the third equation by the sum of itself and -1 times the second equation.
A)
B)
C)
D)
-Replace the third equation by the sum of itself and -1 times the second equation.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
31
Obtain an equivalent system by performing the stated elementary operation on the system.
-Replace the fourth equation by the sum of itself and 3 times the second equation
X-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
2 y-2 z-3 w=8
A)x-2 y+5 z-6 w & =4 \\
4 y-z+4 w & =-5 \\
3 y-4 z+2 w & =-3 \\
14 y-5 z+9 w & =-7
B)x-2 y+5 z-6 w= & 4 \\
12 y-3 z+12 w= & -15 \\
3 y-4 z+2 w= & -3 \\
2 y-2 z-3 w= & 8
C)x-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
12 y+3 z+9 w=-7
D)x-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
-10 y+5 z-15 w=23
-Replace the fourth equation by the sum of itself and 3 times the second equation
X-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
2 y-2 z-3 w=8
A)x-2 y+5 z-6 w & =4 \\
4 y-z+4 w & =-5 \\
3 y-4 z+2 w & =-3 \\
14 y-5 z+9 w & =-7
B)x-2 y+5 z-6 w= & 4 \\
12 y-3 z+12 w= & -15 \\
3 y-4 z+2 w= & -3 \\
2 y-2 z-3 w= & 8
C)x-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
12 y+3 z+9 w=-7
D)x-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
-10 y+5 z-15 w=23

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system by back substitution.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the system by back substitution.
-6 x+2 y-3 z-5 w & =12
Y-2 z-5 w & =-11
5 z-2 w & =-24
4 w & =8
A)
B)
C)
D)
-6 x+2 y-3 z-5 w & =12
Y-2 z-5 w & =-11
5 z-2 w & =-24
4 w & =8
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
34
Write an augmented matrix for the system of equations.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
35
Write an augmented matrix for the system of equations.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
36
Write an augmented matrix for the system of equations.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
37
Write an augmented matrix for the system of equations.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
38
Write the system of equations associated with the augmented matrix. Do not solve.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
39
Write the system of equations associated with the augmented matrix. Do not solve.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
40
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
A)
B)
C)
D)
-Replace by
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
41
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
A)
B)
C)
D)
-Replace by
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
42
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
A)
B)
C)
D)
-Replace by
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
43
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
A)
B)
C)
D)
-Replace by
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
44
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
A)
B)
C)
D)
-Replace by
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
45
The reduced row echelon form of the augmented matrix of a system of equations is given. Find the solutions of thesystem.
-45
A) for any real number
B)
C)
D) No solution
-45
A) for any real number
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
46
The reduced row echelon form of the augmented matrix of a system of equations is given. Find the solutions of thesystem.
-
A)
B) for any real number
C)
D) No solution
-
A)
B) for any real number
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
47
The reduced row echelon form of the augmented matrix of a system of equations is given. Find the solutions of thesystem.
-
A) , w) for any real number
B) No solution
C)
D) , w) for any real number
-
A) , w) for any real number
B) No solution
C)
D) , w) for any real number

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
48
The reduced row echelon form of the augmented matrix of a system of equations is given. Find the solutions of thesystem.
-
A) for any real number
B)
C)
D) No solution
-
A) for any real number
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
49
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A)I nconsistent
B) Independent
C) Dependent
-
A)I nconsistent
B) Independent
C) Dependent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
50
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Dependent
B) Inconsistent
C) Independent
-
A) Dependent
B) Inconsistent
C) Independent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
51
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Dependent
B) Independent
C) Inconsistent
-
A) Dependent
B) Independent
C) Inconsistent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
52
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Independent
B) Inconsistent
C) Dependent
-
A) Independent
B) Inconsistent
C) Dependent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
53
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Dependent
B) Independent
C) Inconsistent
-
A) Dependent
B) Independent
C) Inconsistent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
54
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Dependent
B) Independent
C) Inconsistent
-
A) Dependent
B) Independent
C) Inconsistent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
55
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Dependent
B) Inconsistent
C) Independent
-
A) Dependent
B) Inconsistent
C) Independent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
56
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Independent
B) Inconsistent
C) Dependent
-
A) Independent
B) Inconsistent
C) Dependent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
57
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
A) Independent
B) Inconsistent
C) Dependent
-
A) Independent
B) Inconsistent
C) Dependent

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A)
B)
C) No solution
D) for any real number
-
A)
B)
C) No solution
D) for any real number

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
66
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
67
Use the Gauss-Jordan method to solve the system of equations.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
68
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
69
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
70
Use the Gauss-Jordan method to solve the system of equations.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
71
Use the Gauss-Jordan method to solve the system of equations.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
72
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
73
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
74
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
75
Use the Gauss-Jordan method to solve the system of equations.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
76
Use the Gauss-Jordan method to solve the system of equations.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the problem by writing and solving a suitable system of equations.
-Alan invests a total of in three different ways. He invests one part in a mutual fund which in the first year has a return of . He invests the second part in a government bond at per year. The third part he puts in the bank at per year. He invests twice as much in the mutual fund as in the bank. The first year Alan's investments bring a total return of . How much did he invest in each way?
A)m utual fund: ; bond: : bank:
B)m utual fund: ; bond: : bank:
C)m utual fund: ; bond: : bank:
D)m utual fund: ; bond: : bank:
-Alan invests a total of in three different ways. He invests one part in a mutual fund which in the first year has a return of . He invests the second part in a government bond at per year. The third part he puts in the bank at per year. He invests twice as much in the mutual fund as in the bank. The first year Alan's investments bring a total return of . How much did he invest in each way?
A)m utual fund: ; bond: : bank:
B)m utual fund: ; bond: : bank:
C)m utual fund: ; bond: : bank:
D)m utual fund: ; bond: : bank:

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem by writing and solving a suitable system of equations.
-Julia is preparing a meal by combining three ingredients. One unit of each ingredient provides the following quantities (in grams) of carbohydrates, fat, and protein.

Ideally the meal should contain 25 grams of protein, 35 grams of carbohydrates, and 13 grams of fat. How many units of each ingredient should Julia use?
A) 2 grams of ingredient grams of ingredient grams of ingredient
B) 3 grams of ingredient , 4 grams of ingredient , 2 grams of ingredient
C) 3 grams of ingredient , 2 grams of ingredient grams of ingredient
D) 4 grams of ingredient grams of ingredient grams of ingredient
-Julia is preparing a meal by combining three ingredients. One unit of each ingredient provides the following quantities (in grams) of carbohydrates, fat, and protein.

Ideally the meal should contain 25 grams of protein, 35 grams of carbohydrates, and 13 grams of fat. How many units of each ingredient should Julia use?
A) 2 grams of ingredient grams of ingredient grams of ingredient
B) 3 grams of ingredient , 4 grams of ingredient , 2 grams of ingredient
C) 3 grams of ingredient , 2 grams of ingredient grams of ingredient
D) 4 grams of ingredient grams of ingredient grams of ingredient

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the problem by writing and solving a suitable system of equations.
-A company produces three models of video cassette player, models , and Z. Each model machine requires 3.2 hours of electronics work, 2.8 hours of assembly time, and 4.4 hours of quality assurance time. Each model machine requires 5.2 hours of electronics work, 4.4 hours of assembly time, and 5.2 hours of quality assurance time. Each model machine requires 5.2 hours of electronics work, 3.2 hours of assembly time, and 3.8 hours of quality assurance time. There are 440 hours available each week for electronics, 346 hours for assembly, and 453 hours for quality assurance. How many of each model should be produced each week if all available time must be used?
A) 38 model , 37 model Y, 25 model
B) 41 model X, 35 model Y, 24 model Z
C) 40 model , 30 model model
D) 40 model , 35 model Y, 25 model Z
-A company produces three models of video cassette player, models , and Z. Each model machine requires 3.2 hours of electronics work, 2.8 hours of assembly time, and 4.4 hours of quality assurance time. Each model machine requires 5.2 hours of electronics work, 4.4 hours of assembly time, and 5.2 hours of quality assurance time. Each model machine requires 5.2 hours of electronics work, 3.2 hours of assembly time, and 3.8 hours of quality assurance time. There are 440 hours available each week for electronics, 346 hours for assembly, and 453 hours for quality assurance. How many of each model should be produced each week if all available time must be used?
A) 38 model , 37 model Y, 25 model
B) 41 model X, 35 model Y, 24 model Z
C) 40 model , 30 model model
D) 40 model , 35 model Y, 25 model Z

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the problem by writing and solving a suitable system of equations.
-Barges from ports and went to cities and . sent 30 barges and sent 8 . City A needs 21 barges and B needs 17. Shipping costs from to from to from to , and from to B. was spent. How many barges went where?
A)
B)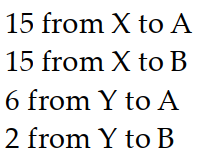
C)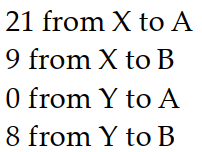
D)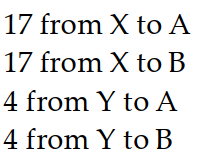
-Barges from ports and went to cities and . sent 30 barges and sent 8 . City A needs 21 barges and B needs 17. Shipping costs from to from to from to , and from to B. was spent. How many barges went where?
A)

B)
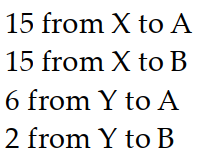
C)
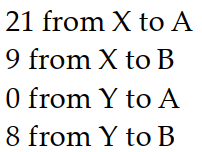
D)
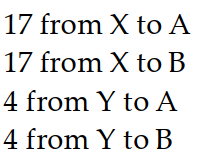

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck


