Exam 6: Systems of Linear Equations and Matrices
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
C
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
C
Find the inverse, if it exists, of the given matrix.
-
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
(True/False)
4.8/5  (35)
(35)
Find the order of the matrix product and the product , whenever the products exist.
- is , B is .
(Multiple Choice)
4.9/5  (33)
(33)
Use the Gauss-Jordan method to solve the system of equations.
-
(Multiple Choice)
4.8/5  (31)
(31)
Obtain an equivalent system by performing the stated elementary operation on the system.
-Multiply the third equation by .
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem by writing and solving a suitable system of equations.
-Julia is preparing a meal by combining three ingredients. One unit of each ingredient provides the following quantities (in grams) of carbohydrates, fat, and protein.
 Ideally the meal should contain 25 grams of protein, 35 grams of carbohydrates, and 13 grams of fat. How many units of each ingredient should Julia use?
Ideally the meal should contain 25 grams of protein, 35 grams of carbohydrates, and 13 grams of fat. How many units of each ingredient should Julia use?
(Multiple Choice)
4.9/5  (28)
(28)
Write the system of equations associated with the augmented matrix. Do not solve.
-
(Multiple Choice)
4.8/5  (37)
(37)
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
(Multiple Choice)
4.9/5  (50)
(50)
Solve the problem.
-Su ppose the following matrix represents the input-output matrix of a primitive economy. How much of each commodity should be produced to produce 15 bushels of yams and 4 pigs?
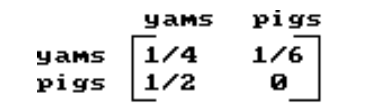
(Multiple Choice)
4.9/5  (41)
(41)
Use the Gauss-Jordan method to solve the system of equations.
-
(Multiple Choice)
4.8/5  (46)
(46)
The diagram shows the roads connecting four cities.
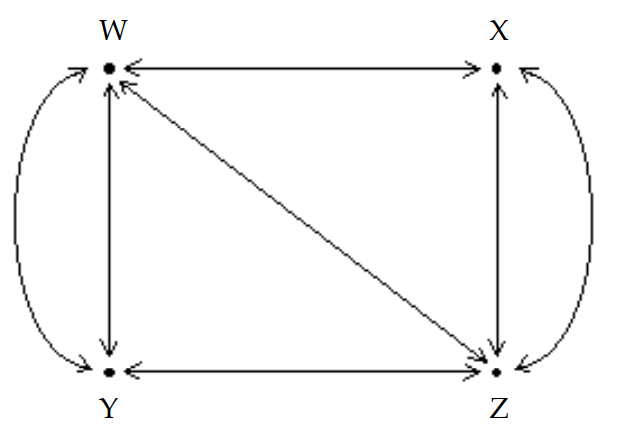 The matrix A below represents the number of routes between each pair of cities without passing through another city.
The matrix A below represents the number of routes between each pair of cities without passing through another city.
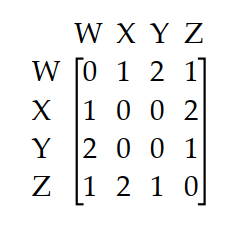 Calculate . What information is given by the entry in row 2 , column 3 of ?
Calculate . What information is given by the entry in row 2 , column 3 of ?
(Multiple Choice)
4.8/5  (31)
(31)
Write the word or phrase that best completes each statement or answers thequestion.
-A simplified economy has only two industries, the electric company and the gas company. Each dollar's worth of the electric company's output requires 0.20 of its own output and 0.4 of the gas company's output. Each dollar's worth of the gas company's output requires 0.50 of its own output and 0.7 of the electric company's output. What should the production of electricity and gas be (in dollars) if there is a million demand for electricity and a million demand for gas?
(Short Answer)
5.0/5  (36)
(36)
Write a system of equations and use the inverse of the coefficient matrix to solve the system.
-A bakery sells three types of cakes, each requiring the amount of ingredients shown.
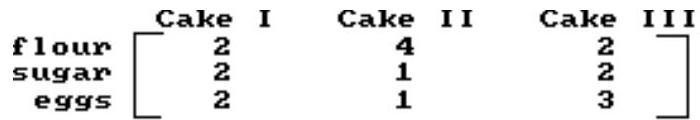 To fill its orders for these cakes, the bakery used 72 cups of flour, 48 cups of sugar, and 54 eggs. How many cakes of each type were made?
To fill its orders for these cakes, the bakery used 72 cups of flour, 48 cups of sugar, and 54 eggs. How many cakes of each type were made?
(Multiple Choice)
4.8/5  (30)
(30)
Showing 1 - 20 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)