Deck 12: Applications of the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/220
Play
Full screen (f)
Deck 12: Applications of the Derivative
1
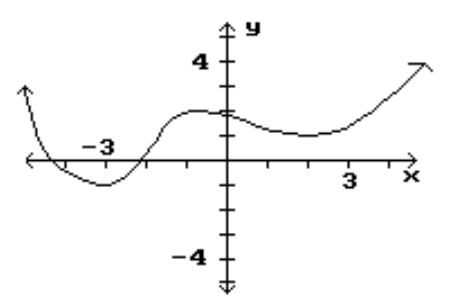
Find the location and value of each local extremum for the function.
-
A)
B)
C)
D)
-

A)
B)
C)
D)
2
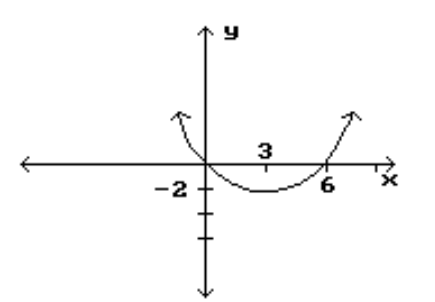
Find the location and value of each local extremum for the function.
-
A)
B)
C)
D)
-

A)
B)
C)
D)
3
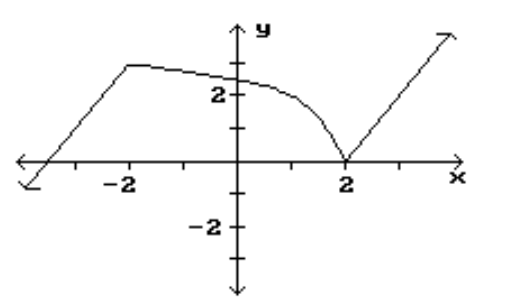
Find the location and value of each local extremum for the function.
-
A)
B) None
C)
D)
-

A)
B) None
C)
D)
4
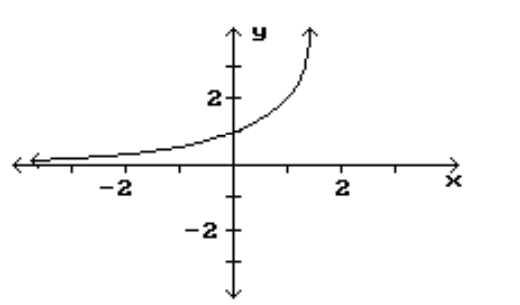
Find the location and value of each local extremum for the function.
-
A)
B)
C) None
D)
-

A)
B)
C) None
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
5
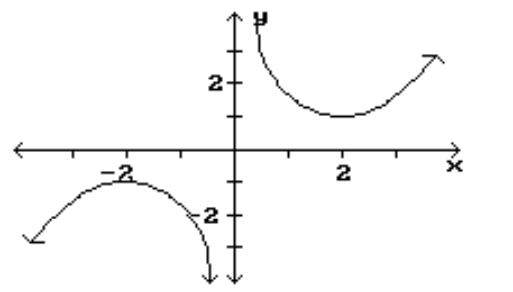
Find the location and value of each local extremum for the function.
-
A)
B)
C) None
D)
-

A)
B)
C) None
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
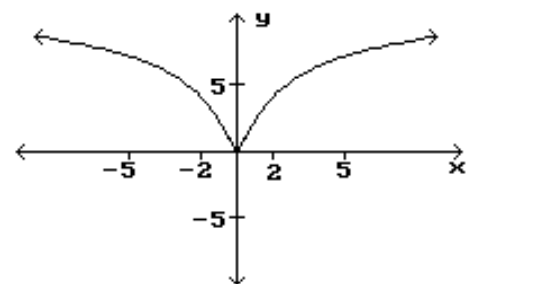
6
Find the location and value of each local extremum for the function.
-
A) None
B)
C)
D)
-

A) None
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
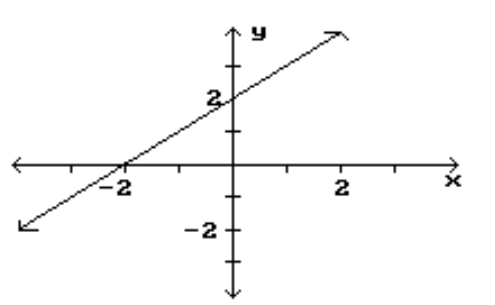
7
Find the location and value of each local extremum for the function.
-
A) None
B)
C)
D)
-

A) None
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
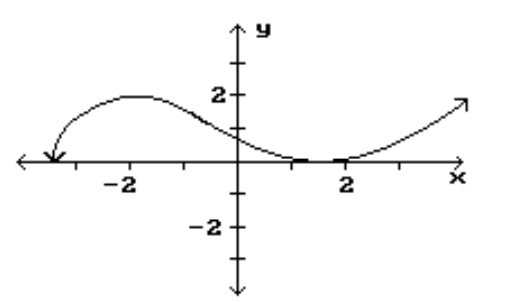
8
Find the location and value of each local extremum for the function.
-
A)
B)
C)
D) None
-

A)
B)
C)
D) None

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
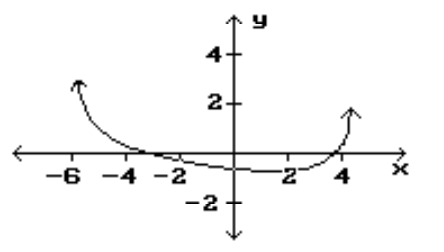
9
Find the location and value of each local extremum for the function.
-
A)
B)
C)
D) None
-

A)
B)
C)
D) None

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
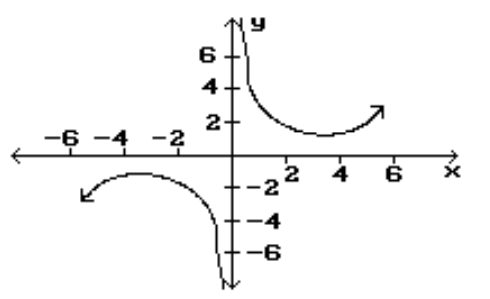
10
Find the location and value of each local extremum for the function.
-
A)
B)
C)
D) None
-

A)
B)
C)
D) None

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
11
Identify the intervals where the function is changing as requested.
-Increasing
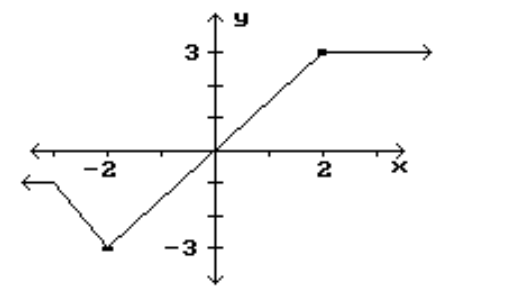
A)
B)
C)
D)
-Increasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
12
Identify the intervals where the function is changing as requested.
-Decreasing
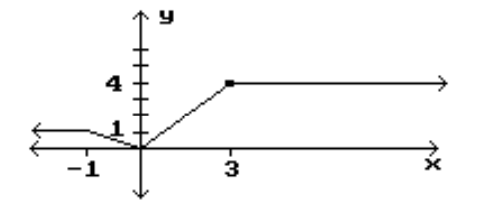
A)
B)
C)
D)
-Decreasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
13
Identify the intervals where the function is changing as requested.
-Increasing
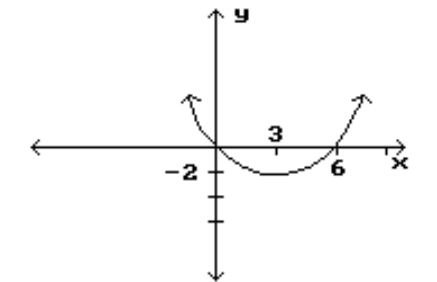
A)
B)
C)
D)
-Increasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
14
Identify the intervals where the function is changing as requested.
-Increasing
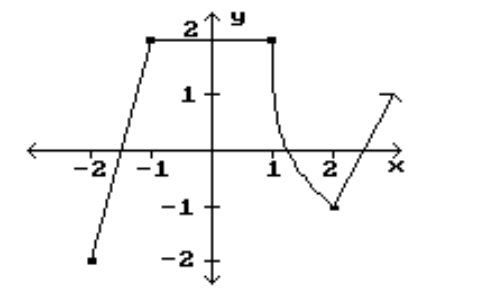
A)
B)
C)
D)
-Increasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
15
Identify the intervals where the function is changing as requested.
-Increasing
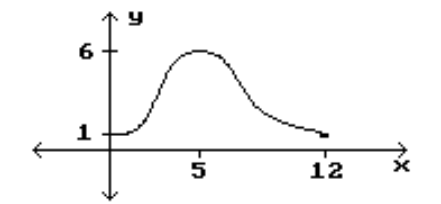
A)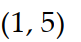
B)
C)
D)
-Increasing

A)
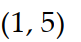
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
16
Identify the intervals where the function is changing as requested.
-Increasing
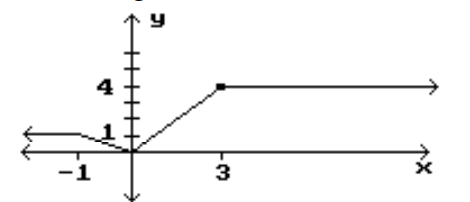
A)
B)
C)
D)
-Increasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
17
Identify the intervals where the function is changing as requested.
-Decreasing
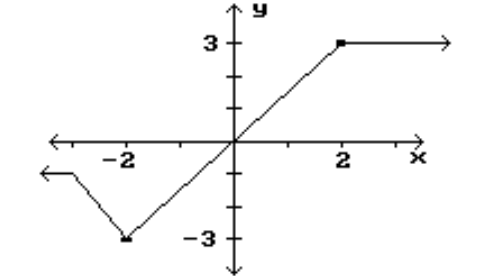
A)
B)
C)
D)
-Decreasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
18
Identify the intervals where the function is changing as requested.
-Decreasing
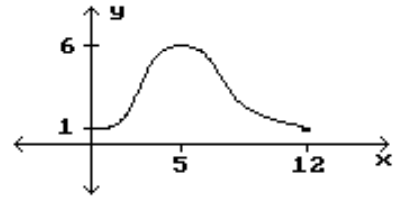
A)
B)
C)
D)
-Decreasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
19
Identify the intervals where the function is changing as requested.
-Decreasing
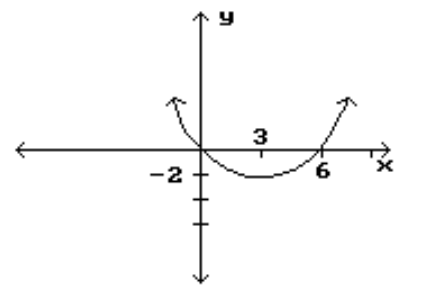
A)
B)
C)
D)
-Decreasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
20
Identify the intervals where the function is changing as requested.
-Decreasing
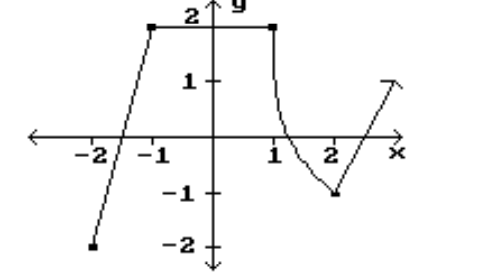
A)
B)
C)
D)
-Decreasing

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
21
Find the largest open interval where the function is changing as requested.
-Increasing
A)
B)
C)
D)
-Increasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
22
Find the largest open interval where the function is changing as requested.
-Increasing
A)
B)
C)
D)
-Increasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
23
Find the largest open interval where the function is changing as requested.
-Increasing
A)
B)
C)
D)
-Increasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
24
Find the largest open interval where the function is changing as requested.
-Increasing
A)
B)
C)
D)
-Increasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
25
Find the largest open interval where the function is changing as requested.
-Increasing
A)
B)
C)
D)
-Increasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
26
Find the largest open interval where the function is changing as requested.
-Decreasing
A)
B)
C)
D)
-Decreasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
27
Find the largest open interval where the function is changing as requested.
-Decreasing
A)
B)
C)
D)
-Decreasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
28
Find the largest open interval where the function is changing as requested.
-Decreasing
A)
B)
C)
D)
-Decreasing
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
29
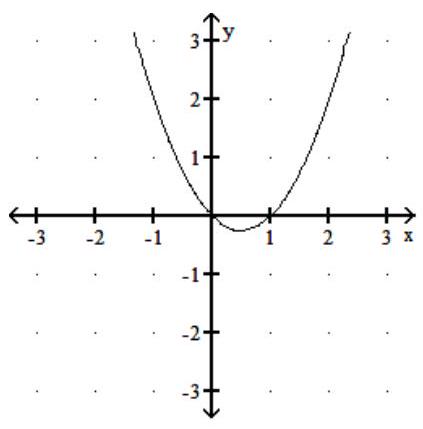
The graph of the derivative function is given. Find the critical numbers of the function .
-
A) 1
B) 0.5
C) 0
D) 0,1
-

A) 1
B) 0.5
C) 0
D) 0,1

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
30
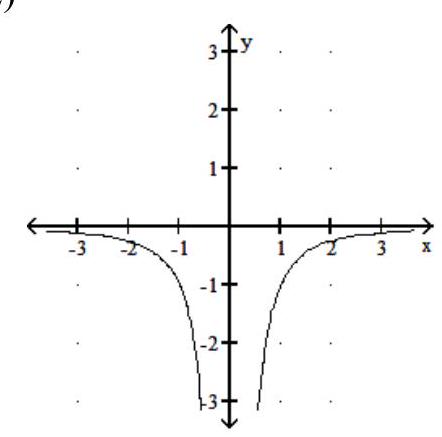
The graph of the derivative function is given. Find the critical numbers of the function .
-
A)
B)
C) none
D) 0
-

A)
B)
C) none
D) 0

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
31
The graph of the derivative function is given. Find the critical numbers of the function .
-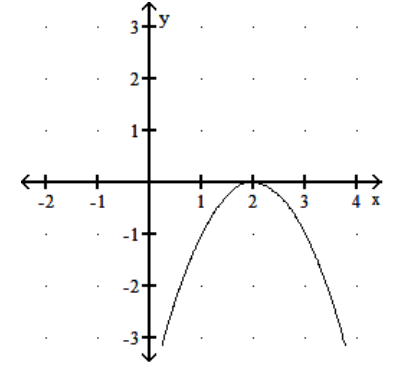
A) 2
B) 0,2
C)
D) 0
-

A) 2
B) 0,2
C)
D) 0

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
32
The graph of the derivative function is given. Find the critical numbers of the function .
-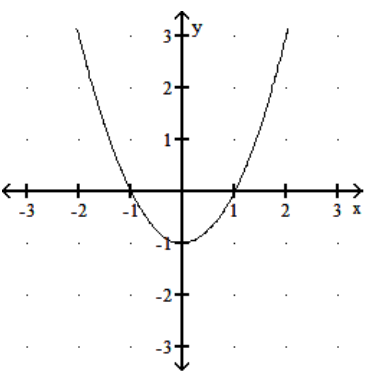
A) -
B)
C) -1
D) 0
-

A) -
B)
C) -1
D) 0

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
33
The graph of the derivative function is given. Find the critical numbers of the function .
-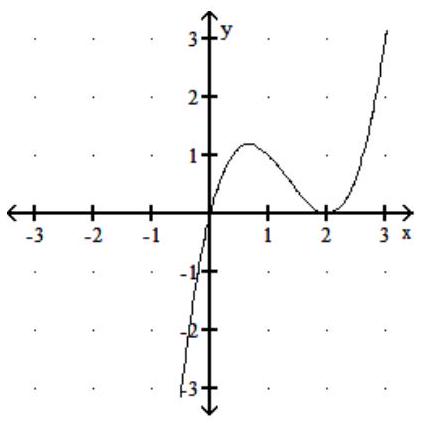
A) 0,2
B)
C)
D) none
-

A) 0,2
B)
C)
D) none

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
34
Determine the location of each local extremum of the function.
-
A) Local maximum at 3 ; local minimum at 4
B) Local maximum at -4 ; local minimum at -3
C) No local extrema
D) Local extremum at 3.5
-
A) Local maximum at 3 ; local minimum at 4
B) Local maximum at -4 ; local minimum at -3
C) No local extrema
D) Local extremum at 3.5

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
35
Determine the location of each local extremum of the function.
-
A) Local maximum at 4 ; local minimum at -3
B) Local maximum at -4 ; local minimum at 3
C) Local maximum at 3 ; local minimum at -4
D) Local maximum at -3 ; local minimum at 4
-
A) Local maximum at 4 ; local minimum at -3
B) Local maximum at -4 ; local minimum at 3
C) Local maximum at 3 ; local minimum at -4
D) Local maximum at -3 ; local minimum at 4

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
36
Determine the location of each local extremum of the function.
-
A) Local maxima at -3 and 4 ; local minimum at 3
B) Local maximum at -3 ; local minimum at 4
C) Local maxima at 3 and -4 ; local minimum at 3
D) Local maximum at 3 ; local minima at -3 and 4
-
A) Local maxima at -3 and 4 ; local minimum at 3
B) Local maximum at -3 ; local minimum at 4
C) Local maxima at 3 and -4 ; local minimum at 3
D) Local maximum at 3 ; local minima at -3 and 4

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
37
Determine the location of each local extremum of the function.
-
A) Local maximum at ; local minimum at 2
B) Local maximum at ; local minimum at -1
C) Local maximum at -2 ; local minimum at
D) Local maximum at 1 ; local minimum at 0.67
-
A) Local maximum at ; local minimum at 2
B) Local maximum at ; local minimum at -1
C) Local maximum at -2 ; local minimum at
D) Local maximum at 1 ; local minimum at 0.67

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
38
Determine the location of each local extremum of the function.
-
A) Local minimum at 3
B) Local maximum at 3
C) Local maximum at 3 ; local minimum at -3
D) No local extrema
-
A) Local minimum at 3
B) Local maximum at 3
C) Local maximum at 3 ; local minimum at -3
D) No local extrema

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
39
Use the first derivative test to determine the location of each local extremum and the value of the function at thatextremum.
-
A) No local extrema
B) Local maximum at
C) Local minimum at
D) Local minimum at
-
A) No local extrema
B) Local maximum at
C) Local minimum at
D) Local minimum at

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
40
Use the first derivative test to determine the location of each local extremum and the value of the function at thatextremum.
-
A) Local maximum at
B) No local extrema
C) Local minimum at
D) Local minimum at
-
A) Local maximum at
B) No local extrema
C) Local minimum at
D) Local minimum at

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
41
Use the first derivative test to determine the location of each local extremum and the value of the function at thatextremum.
-
A) No local extrema
B) Local minimum at
C) Local maximum at
D) Local minimum at
-
A) No local extrema
B) Local minimum at
C) Local maximum at
D) Local minimum at

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
42
Use the first derivative test to determine the location of each local extremum and the value of the function at thatextremum.
-
A) No local extrema
B) Local maximum at ; local minimum at
C) Local maximum at ; local minima at and
D) Local maximum at ; local minimum at
-
A) No local extrema
B) Local maximum at ; local minimum at
C) Local maximum at ; local minima at and
D) Local maximum at ; local minimum at

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
43
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maximum at -98.442 ; approximate local minimum at -1.558
B) Approximate local maximum at 1.558 ; approximate local minimum at 98.442
C) Approximate local minimum at 1.558 ; approximate local maximum at 98.442
D) Approximate local minimum at -98.442; approximate local maximum at -1.558
-
A) Approximate local maximum at -98.442 ; approximate local minimum at -1.558
B) Approximate local maximum at 1.558 ; approximate local minimum at 98.442
C) Approximate local minimum at 1.558 ; approximate local maximum at 98.442
D) Approximate local minimum at -98.442; approximate local maximum at -1.558

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
44
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maximum at 1.735; approximate local minima at -6.777 and 12.542
B) Approximate local maximum at 1.801; approximate local minima at -6.723 and 12.642
C) Approximate local maximum at 1.817; approximate local minima at -6.837 and 12.465
D) Approximate local maximum at 1.815 ; approximate local minima at -6.778 and 12.597
-
A) Approximate local maximum at 1.735; approximate local minima at -6.777 and 12.542
B) Approximate local maximum at 1.801; approximate local minima at -6.723 and 12.642
C) Approximate local maximum at 1.817; approximate local minima at -6.837 and 12.465
D) Approximate local maximum at 1.815 ; approximate local minima at -6.778 and 12.597

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
45
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maximum at 1.577; approximate local minima at -3.108 and 3.721
B) Approximate local maximum at 1.536 ; approximate local minima at -3.157 and 3.69
C) Approximate local maximum at 1.604; approximate local minima at -3.089 and 3.735
D) Approximate local maximum at 1.671 ; approximate local minima at -3.163 and 3.704
-
A) Approximate local maximum at 1.577; approximate local minima at -3.108 and 3.721
B) Approximate local maximum at 1.536 ; approximate local minima at -3.157 and 3.69
C) Approximate local maximum at 1.604; approximate local minima at -3.089 and 3.735
D) Approximate local maximum at 1.671 ; approximate local minima at -3.163 and 3.704

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
46
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maximum at -0.944 ; approximate local minima at -3.192 and 7.136
B) Approximate local maximum at 1.02 ; approximate local minima at -3.167 and 7.046
C) Approximate local maximum at 0.852 ; approximate local minima at -3.234 and 7.127
D) Approximate local maximum at 0.935 ; approximate local minima at -3.119 and 7.198
-
A) Approximate local maximum at -0.944 ; approximate local minima at -3.192 and 7.136
B) Approximate local maximum at 1.02 ; approximate local minima at -3.167 and 7.046
C) Approximate local maximum at 0.852 ; approximate local minima at -3.234 and 7.127
D) Approximate local maximum at 0.935 ; approximate local minima at -3.119 and 7.198

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
47
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maximum at 0.353 ; approximate local minimum at -12.638
B) Approximate local maximum at 0.29 ; approximate local minima at -0.572 and -12.568
C) Approximate local maximum at 0.379 ; approximate local minimum at 12.565
D) Approximate local maximum at 0.379 ; approximate local minima at -0.472 and 12.565
-
A) Approximate local maximum at 0.353 ; approximate local minimum at -12.638
B) Approximate local maximum at 0.29 ; approximate local minima at -0.572 and -12.568
C) Approximate local maximum at 0.379 ; approximate local minimum at 12.565
D) Approximate local maximum at 0.379 ; approximate local minima at -0.472 and 12.565

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
48
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maxima at -41.038 and -0.368 ; approximate local minima at -0.564 and 1.858
B) Approximate local maxima at -41.075 and -0.343 ; approximate local minima at -0.616 and 2.021
C) Approximate local maxima at -41.132 and -0.273 ; approximate local minima at -0.547 and 1.952
D) Approximate local maxima at -41.207 and -0.249 ; approximate local minima at -0.513 and 1.976
-
A) Approximate local maxima at -41.038 and -0.368 ; approximate local minima at -0.564 and 1.858
B) Approximate local maxima at -41.075 and -0.343 ; approximate local minima at -0.616 and 2.021
C) Approximate local maxima at -41.132 and -0.273 ; approximate local minima at -0.547 and 1.952
D) Approximate local maxima at -41.207 and -0.249 ; approximate local minima at -0.513 and 1.976

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
49
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
A) Approximate local maxima at -1.861 and 2.247 ; approximate local minimum at 0.423
B) Approximate local maxima at -1.85 and 2.165 ; approximate local minima at 0.445 and 79.11
C) Approximate local maxima at -1.864 and 2.282 ; approximate local minima at 0.373 and 79.195
D) Approximate local maxima at -1.861 and 2.247 ; approximate local minima at 0.423 and 79.192
-
A) Approximate local maxima at -1.861 and 2.247 ; approximate local minimum at 0.423
B) Approximate local maxima at -1.85 and 2.165 ; approximate local minima at 0.445 and 79.11
C) Approximate local maxima at -1.864 and 2.282 ; approximate local minima at 0.373 and 79.195
D) Approximate local maxima at -1.861 and 2.247 ; approximate local minima at 0.423 and 79.192

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
50
Solve each problem.
-If the price charged for a bolt is cents, then thousand bolts will be sold in a certain hardware store, where . How many bolts must be sold to maximize revenue?
A) 875 thousand bolts
B) 1750 thousand bolts
C) 875 bolts
D) 1750 bolts
-If the price charged for a bolt is cents, then thousand bolts will be sold in a certain hardware store, where . How many bolts must be sold to maximize revenue?
A) 875 thousand bolts
B) 1750 thousand bolts
C) 875 bolts
D) 1750 bolts

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
51
Solve each problem.
-The price of a certain computer system decreases immediately after its introduction and then increases. If the price is estimated by the formula , where is the time in months from its introduction, find the time until the minimum price is reached.
A) 19.2 months
B) 38.5 months
C) 12.5 months
D) 9.6 months
-The price of a certain computer system decreases immediately after its introduction and then increases. If the price is estimated by the formula , where is the time in months from its introduction, find the time until the minimum price is reached.
A) 19.2 months
B) 38.5 months
C) 12.5 months
D) 9.6 months

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
52
Solve each problem.
-A rectangular field is to be enclosed on four sides with a fence. Fencing costs per foot for two opposite sides, and per foot for the other two sides. Find the dimensions of the field of area that would be the cheapest to enclose.
A) by
B) by
C) by
D) by
-A rectangular field is to be enclosed on four sides with a fence. Fencing costs per foot for two opposite sides, and per foot for the other two sides. Find the dimensions of the field of area that would be the cheapest to enclose.
A) by
B) by
C) by
D) by

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
53
Solve each problem.
-The cost of a computer system increases with increased processor speeds. The cost of a system as a function of processor speed is estimated as , where is the processor speed in MHz. Find the processor speed for which cost is at a minimum.
A)
B)
C)
D)
-The cost of a computer system increases with increased processor speeds. The cost of a system as a function of processor speed is estimated as , where is the processor speed in MHz. Find the processor speed for which cost is at a minimum.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
54
Solve each problem.
-The velocity of a particle (in ) is given by , where is the time (in seconds) for which it has traveled. Find the time at which the velocity is at a minimum.
A)
B)
C)
D)
-The velocity of a particle (in ) is given by , where is the time (in seconds) for which it has traveled. Find the time at which the velocity is at a minimum.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
55
Solve each problem.
-Find the dimensions that produce the maximum floor area for a one-story house that is rectangular in shape and has a perimeter of .
A)
B)
C)
D)
-Find the dimensions that produce the maximum floor area for a one-story house that is rectangular in shape and has a perimeter of .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
56
Solve each problem.
-An architect needs to design a rectangular room with an area of . What dimensions should she use in order to minimize the perimeter?
A)
B)
C)
D)
-An architect needs to design a rectangular room with an area of . What dimensions should she use in order to minimize the perimeter?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
57
Solve each problem.
-A piece of molding long is to be cut to form a rectangular picture frame. What dimensions will enclose the largest area?
A)
B)
C)
D)
-A piece of molding long is to be cut to form a rectangular picture frame. What dimensions will enclose the largest area?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
58
Solve each problem.
-Find two numbers whose sum is 440 and whose product is as large as possible.
A) 219 and 221
B) 1 and 439
C) 220 and 220
D) 10 and 430
-Find two numbers whose sum is 440 and whose product is as large as possible.
A) 219 and 221
B) 1 and 439
C) 220 and 220
D) 10 and 430

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
59
Solve each problem.
-Find the dimensions of the rectangular field of maximum area that can be made from of fencing material.
A) by
B) by
C) by
D) by
-Find the dimensions of the rectangular field of maximum area that can be made from of fencing material.
A) by
B) by
C) by
D) by

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate at the point.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
-Find the velocity function if .
A)
B)
C)
D)
-Find the velocity function if .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
-Find the acceleration function if .
A)
B)
C)
D)
-Find the acceleration function if .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.
-Find the velocity function if .
A)
B)
C)
D)
-Find the velocity function if .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
-Find the acceleration function if .
A)
B)
C)
D)
-Find the acceleration function if .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
74
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
75
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
76
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
77
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
78
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
79
Find the coordinates of the points of inflection for the function.
-
A)
B)
C)
D) There are no points of inflection.
-
A)
B)
C)
D) There are no points of inflection.

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck
80
Find the coordinates of the points of inflection for the function.
-
A)
B)
C)
D) There are no points of inflection.
-
A)
B)
C)
D) There are no points of inflection.

Unlock Deck
Unlock for access to all 220 flashcards in this deck.
Unlock Deck
k this deck


