Exam 12: Applications of the Derivative
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Find the largest open interval where the function is changing as requested.
-Increasing
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
A
Solve the problem.
-The correlation between respiratory rate and body mass in the first three years of life can be expressed by the function
Where is the body weight (in ) and ) is the respiratory rate (in breaths per minute). Find using implicit differentiation.
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
D
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
B
Solve the problem.
-The price of a certain computer system decreases immediately after its introduction and then increases. If the price is estimated by the formula , where is the time in months from its introduction, find the time until the minimum price is reached. Round to the nearest tenth if necessary.
(Multiple Choice)
4.8/5  (39)
(39)
Determine the location of each local extremum of the function.
-
(Multiple Choice)
4.7/5  (34)
(34)
Solve each problem.
-A piece of molding long is to be cut to form a rectangular picture frame. What dimensions will enclose the largest area?
(Multiple Choice)
4.8/5  (38)
(38)
Identify the intervals where the function is changing as requested.
-Increasing
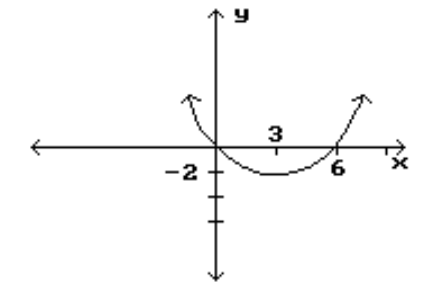
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-A man tall walks at a rate of away from a lamppost that is high. At what rate is the length of his shadow changing when he is away from the lamppost?
(Multiple Choice)
4.7/5  (39)
(39)
Determine the location of each local extremum of the function.
-
(Multiple Choice)
4.8/5  (38)
(38)
The rule of the derivative of a function is given. Find the location of all points of inflection of the function .
-
(Multiple Choice)
4.8/5  (32)
(32)
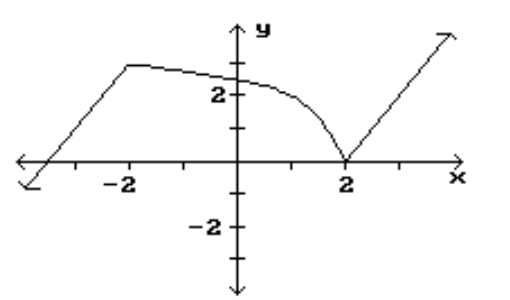
Find the location and value of each local extremum for the function.
-
(Multiple Choice)
4.7/5  (26)
(26)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-A product sells by word of mouth. The company that produces the product has noticed that revenue from sales is given by , where is the number of units produced and sold. If the revenue keeps changing at a rate of per month, how fast is the rate of sales changing when 300 units have been made and sold? (Round to the nearest dollar per month.)
(Multiple Choice)
4.8/5  (33)
(33)
Find the absolute extremum within the specified domain.
-Maximum of
(Multiple Choice)
5.0/5  (33)
(33)
A rectangular field is to be enclosed on four sides with a fence. Fencing costs per foot for two opposite sides, and per foot for the other two sides. Find the dimensions of the field of area that would be the cheapest to enclose. Round to the nearest tenth.
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-At a certain copy center, the cost (in dollars) of purchasing thousand printed cards can be approximated by . Use implicit differentiation to find and interpret when and .
(Multiple Choice)
4.8/5  (27)
(27)
Solve each problem.
-A rectangular field is to be enclosed on four sides with a fence. Fencing costs per foot for two opposite sides, and per foot for the other two sides. Find the dimensions of the field of area that would be the cheapest to enclose.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 1 - 20 of 220
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)