Deck 7: Goal Programming and Multiple Objective Optimization
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/62
Play
Full screen (f)
Deck 7: Goal Programming and Multiple Objective Optimization
1
What is the soft constraint form of the following hard constraint?
3X1 + 2 X2 10
A)3X1 + 2 X2 + d1- - d1+ = 10
B)3X1 + 2 X2 + d1- + d1+ = 10
C)3X1 + 2 X2 -d1- - d1+ 10
D)3X1 + 2 X2 + d1- - d1+ 10
3X1 + 2 X2 10
A)3X1 + 2 X2 + d1- - d1+ = 10
B)3X1 + 2 X2 + d1- + d1+ = 10
C)3X1 + 2 X2 -d1- - d1+ 10
D)3X1 + 2 X2 + d1- - d1+ 10
3X1 + 2 X2 + d1- - d1+ = 10
2
Suppose that the first goal in a GP problem is to make 3 X1 + 4 X2 approximately equal to 36. Using the deviational variables d1- and d1+, what constraint can be used to express this goal?
A)3 X1 + 4 X2 + d1- -d1+ 36
B)3 X1 + 4 X2 -d1- - d1+ = 36
C)3 X1 + 4 X2 + d1- + d1+ = 36
D)3 X1 + 4 X2 + d1- - d1+ = 36
A)3 X1 + 4 X2 + d1- -d1+ 36
B)3 X1 + 4 X2 -d1- - d1+ = 36
C)3 X1 + 4 X2 + d1- + d1+ = 36
D)3 X1 + 4 X2 + d1- - d1+ = 36
3 X1 + 4 X2 + d1- - d1+ = 36
3
Decision-making problems which can be stated as a collection of desired objectives are known as what type of problem?
A)A non-linear programming problem.
B)An unconstrained programming problem.
C)A goal programming problem.
D)An integer programming problem.
A)A non-linear programming problem.
B)An unconstrained programming problem.
C)A goal programming problem.
D)An integer programming problem.
C
4
A constraint which represents a target value for a problem is called a
A)fuzzy constraint.
B)vague constraint.
C)preference constraint
D)soft constraint
A)fuzzy constraint.
B)vague constraint.
C)preference constraint
D)soft constraint

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that X1 equals 4. What are the values for d1+ and d1- in the following constraint? X1 + d11-- d1+ = 8
A)d1- = 4, d1+ = 0
B)d1- = 0, d1+ = 4
C)d1- = 4, d1+ = 4
D)d1- = 8, d1+ = 0
A)d1- = 4, d1+ = 0
B)d1- = 0, d1+ = 4
C)d1- = 4, d1+ = 4
D)d1- = 8, d1+ = 0

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following formulas is a deviation-minimizing objective function for a goal programming problem?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
7
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.
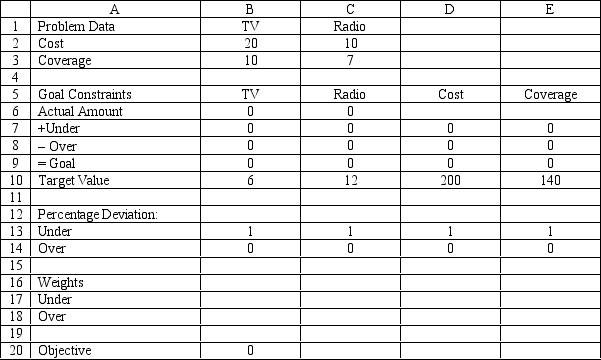
-Refer to Exhibit 7.1. What formula goes in cell B9?
A)=SUM(B6:B8)
B)=B6+B7-B8
C)=B6-B7+B8
D)=B10-B8

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
8
The RHS value of a goal constraint is referred to as the
A)target value.
B)constraint value.
C)objective value.
D)desired value.
A)target value.
B)constraint value.
C)objective value.
D)desired value.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
9
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.

-Refer to Exhibit 7.1. What formula goes in cell D6?
A)=SUMPRODUCT(B2:B3,B6:B7)
B)=B2*C2+B6*C6
C)=SUMPRODUCT(B2:C2,B10:C10)
D)=SUMPRODUCT(B2:C2,B6:C6)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
10
The di+, di- variables are referred to as
A)objective variables.
B)goal variables.
C)target variables.
D)deviational variables.
A)objective variables.
B)goal variables.
C)target variables.
D)deviational variables.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
11
What is the meaning of the ti term in this objective function for a goal programming problem? 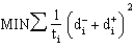
A)The time required for each decision variable.
B)The percent of goal i met.
C)The coefficient for the ith decision variable
D)The target value for goal i.
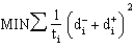
A)The time required for each decision variable.
B)The percent of goal i met.
C)The coefficient for the ith decision variable
D)The target value for goal i.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
12
Goal programming differs from linear programming or integer linear programming is that
A)goal programming provides for multiple objectives.
B)goal programming excludes hard constraints.
C)with goal programming we iterate until an acceptable solution is obtained.
D)goal programming requires fewer variables.
A)goal programming provides for multiple objectives.
B)goal programming excludes hard constraints.
C)with goal programming we iterate until an acceptable solution is obtained.
D)goal programming requires fewer variables.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
13
A constraint which cannot be violated is called a
A)binding constraint.
B)hard constraint.
C)definite constraint.
D)required constraint.
A)binding constraint.
B)hard constraint.
C)definite constraint.
D)required constraint.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following is false regarding a goal constraint?
A)A goal constraint allows us to determine how close a given solution comes to achieving a goal.
B)A goal constraint will always contain two deviational variables.
C)Deviation variables are non-negative.
D)If two deviation variables are used in a constraint at least one will have a value of zero.
A)A goal constraint allows us to determine how close a given solution comes to achieving a goal.
B)A goal constraint will always contain two deviational variables.
C)Deviation variables are non-negative.
D)If two deviation variables are used in a constraint at least one will have a value of zero.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that the first goal in a GP problem is to make 3 X1 + 4 X2 approximately equal to 36. Using the deviational variables d1- and d1+, the following constraint can be used to express this goal. 3 X1 + 4 X2 + d1- - d1+ = 36
If we obtain a solution where X1 = 6 and X2 = 2, what values do the deviational variables assume?
A)d1- = 0, d1+ = 10
B)d1- = 10, d1+ = 0
C)d1- = 5, d1+ = 5
D)d1- = 6, d1+ = 0
If we obtain a solution where X1 = 6 and X2 = 2, what values do the deviational variables assume?
A)d1- = 0, d1+ = 10
B)d1- = 10, d1+ = 0
C)d1- = 5, d1+ = 5
D)d1- = 6, d1+ = 0

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following are true regarding weights assigned to deviational variables?
A)The weights assigned can be negative.
B)The weights assigned must sum to one.
C)The weight assigned to the deviation under a particular goal must be the same as the weight assigned to the deviation above that particular goal.
D)All of these are false.
A)The weights assigned can be negative.
B)The weights assigned must sum to one.
C)The weight assigned to the deviation under a particular goal must be the same as the weight assigned to the deviation above that particular goal.
D)All of these are false.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
17
The di+ variable indicates the amount by which each goal's target value is
A)missed.
B)underachieved.
C)overachieved.
D)overstated.
A)missed.
B)underachieved.
C)overachieved.
D)overstated.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is true regarding goal programming?
A)The objective function is not useful when comparing goal programming solutions.
B)We can place upper bounds on any of the deviation variables.
C)A preemptive goal program involves deviations with arbitrarily large weights.
D)All of these are true.
A)The objective function is not useful when comparing goal programming solutions.
B)We can place upper bounds on any of the deviation variables.
C)A preemptive goal program involves deviations with arbitrarily large weights.
D)All of these are true.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
19
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.

-Refer to Exhibit 7.1. Which of the following is a constraint specified to Risk Solver Platform (RSP) for this model?
A)$B$9:$E$9=$B$6:$E$6
B)$B$9:$E$9<$B$10:$E$10
C)$B$9:$E$9=$B$10:$E$10
D)$B$9:$E$9>$B$10:$E$10

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
20
What weight would be assigned to a neutral deviational variable?
A)0
B)1
C)10
D)100
A)0
B)1
C)10
D)100

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
21
Exhibit 7.3
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel.
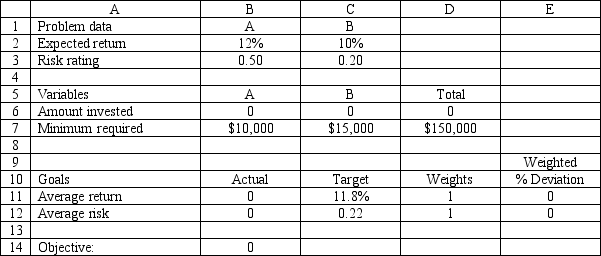
Refer to Exhibit 7.3. Which value should the investor change, and in what direction, if he wants to reduce the risk of the portfolio?
A)D11, increase
B)D12, increase
C)C12, increase
D)D12, decrease
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel.

Refer to Exhibit 7.3. Which value should the investor change, and in what direction, if he wants to reduce the risk of the portfolio?
A)D11, increase
B)D12, increase
C)C12, increase
D)D12, decrease

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
22
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.
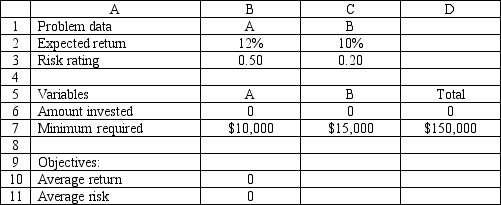
-Refer to Exhibit 7.2. Which cell(s) is(are) the target cells in this model?
A)$B$6:$C$6, $B$10:$B$11
B)$B$6:$C$6
C)$B$6:$D$6
D)$B$10:$B$11

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following MOLP:
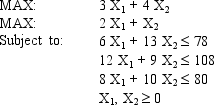 Graph the feasible region for this problem and compute the value of each objective at each extreme point. What are the solutions to each of the component LPs?
Graph the feasible region for this problem and compute the value of each objective at each extreme point. What are the solutions to each of the component LPs? 
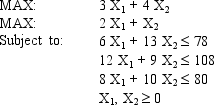 Graph the feasible region for this problem and compute the value of each objective at each extreme point. What are the solutions to each of the component LPs?
Graph the feasible region for this problem and compute the value of each objective at each extreme point. What are the solutions to each of the component LPs? 

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
24
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.

-Refer to Exhibit 7.2. What formula goes in cell B11?
A)=SUMPRODUCT(B2:C2,$B$6:$C$6)/$D$7
B)=B2*C2+B3*C3
C)=SUMPRODUCT(B3:C3,$B$6:$C$6)/$D$7
D)=SUMPRODUCT(B3:C3,$B$6:$C$6)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
25
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.

-Refer to Exhibit 7.2. Which cells are the changing cells in this model?
A)$B$6:$C$6, $B$10:$B$11
B)$B$6:$C$6
C)$B$6:$D$6
D)$B$10:$B$11

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
26
A manager wants to ensure that he does not exceed his budget by more than $1000 in a goal programming problem. If the budget constraint is the third constraint in the goal programming problem which of the following formulas will best ensure that the manager's objective is met?
A)MIN d3+
B)d3- 1000
C)d3+ = 1000
D)d3+ 1000
A)MIN d3+
B)d3- 1000
C)d3+ = 1000
D)d3+ 1000

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
27
The MINIMAX objective
A)yields the smallest possible deviations.
B)minimizes the maximum deviation from any goal.
C)chooses the deviation which has the largest value.
D)maximizes the minimum value of goal attainment.
A)yields the smallest possible deviations.
B)minimizes the maximum deviation from any goal.
C)chooses the deviation which has the largest value.
D)maximizes the minimum value of goal attainment.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
28
If no other feasible solution to a multi-objective linear programming (MOLP) problem allows an increase in any objective without decreasing at least one other objective, the solution is said to be
A)dually optimal.
B)Pareto optimal.
C)suboptimal.
D)maximally optimal.
A)dually optimal.
B)Pareto optimal.
C)suboptimal.
D)maximally optimal.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
29
Goal programming solution feedback indicates that the d4+ level of 50 should not be exceeded in future solution iterations. How should you modify your goal constraint 40 X1 + 20 X2 + d4-+ d4+ = 300
To accommodate this requirement?
A)Increase the RHS value from 300 to 350.
B)Replace the constraint with 40 X1 + 20 X2 350.
C)Do not modify the constraint, add a constraint d4+ 50.
D)Do not modify the constraint, add a constraint d4+ = 50.
To accommodate this requirement?
A)Increase the RHS value from 300 to 350.
B)Replace the constraint with 40 X1 + 20 X2 350.
C)Do not modify the constraint, add a constraint d4+ 50.
D)Do not modify the constraint, add a constraint d4+ = 50.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
30
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.

-Refer to Exhibit 7.1. If the company is very concerned about going over the $200,000 budget, which cell value should change and how should it change?
A)D13, increase
B)D13, decrease
C)D14, increase
D)D14, decrease

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
31
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.

-Refer to Exhibit 7.2. What formula goes in cell B10?
A)=SUMPRODUCT(B2:C2,$B$6:$C$6)/$D$7
B)=B2*C2+B3*C3
C)=SUMPRODUCT(B3:C3,$B$6:$C$6)/$D$7
D)=SUMPRODUCT(B2:C2,$B$6:$C$6)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
32
Exhibit 7.3
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel.

-Refer to Exhibit 7.3. What formula goes in cell E11?
A)=D11*(C11-B11)/C11
B)=(C11-B11)/C11
C)=D11*C11
D)=D11*(C11- B11)
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel.

-Refer to Exhibit 7.3. What formula goes in cell E11?
A)=D11*(C11-B11)/C11
B)=(C11-B11)/C11
C)=D11*C11
D)=D11*(C11- B11)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
33
The decision maker has expressed concern with Goal 1, budget, achievement. He indicated that future candidate solutions should stay under budget. How can you modify your goal programming model to accommodate this change?
A)Make budget a hard constraint in the model.
B)Give d1+ an extremely large weight in the objective function.
C)Remove d1+ from the goal constraint.
D)All of these.
A)Make budget a hard constraint in the model.
B)Give d1+ an extremely large weight in the objective function.
C)Remove d1+ from the goal constraint.
D)All of these.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
34
The primary benefit of a MINIMAX objective function is
A)it yields any feasible solution by changing the weights.
B)it is limited to all corner points.
C)it yields a larger variety of solutions than generally available using an LP method.
D)it makes many of the deviational variables equal to zero.
A)it yields any feasible solution by changing the weights.
B)it is limited to all corner points.
C)it yields a larger variety of solutions than generally available using an LP method.
D)it makes many of the deviational variables equal to zero.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
35
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.

-Refer to Exhibit 7.1. Which cell(s) is(are) the objective cell(s) in this model?
A)$B$20
B)$D$6
C)$E$6
D)$B$13:$E$14, $B$9:$E$9

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
36
Given the following goal constraints
5 X1 + 6 X2 + 7 X3 + d1-- d1+ = 87
3 X1 + X2 + 4 X3 + d2-- d2+ = 37
7 X1 + 3 X2 + 2 X3 + d3- -d3+ = 72
and solution (X1, X2, X3) = (7, 2, 5), what values do the deviational variables assume?
5 X1 + 6 X2 + 7 X3 + d1-- d1+ = 87
3 X1 + X2 + 4 X3 + d2-- d2+ = 37
7 X1 + 3 X2 + 2 X3 + d3- -d3+ = 72
and solution (X1, X2, X3) = (7, 2, 5), what values do the deviational variables assume?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
37
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.

-Refer to Exhibit 7.1. Which cells are the variable cells in this model?
A)$B$6:$C$6, $B$7:$E$8
B)$B$6:$C$6
C)$B$9:$E$9
D)$B$6:$E$8

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
38
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.

-Refer to Exhibit 7.2. What Risk Solver Platform (RSP) constraint involves cells $B$6:$C$6?
A)$B$6:$C$6=$B$7:$C$7
B)$B$6:$C$6 $B$7:$C$7
C)$B$6:$C$6 $B$7:$C$7
D)$B$6:$C$6=$D$7

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
39
An optimization technique useful for solving problems with more than one objective function is
A)dual programming.
B)sensitivity analysis.
C)multi-objective linear programming.
D)goal programming.
A)dual programming.
B)sensitivity analysis.
C)multi-objective linear programming.
D)goal programming.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
40
MINIMAX solutions to multi-objective linear programming (MOLP) problems are
A)dually optimal.
B)Pareto optimal.
C)suboptimal.
D)maximally optimal.
A)dually optimal.
B)Pareto optimal.
C)suboptimal.
D)maximally optimal.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
41
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
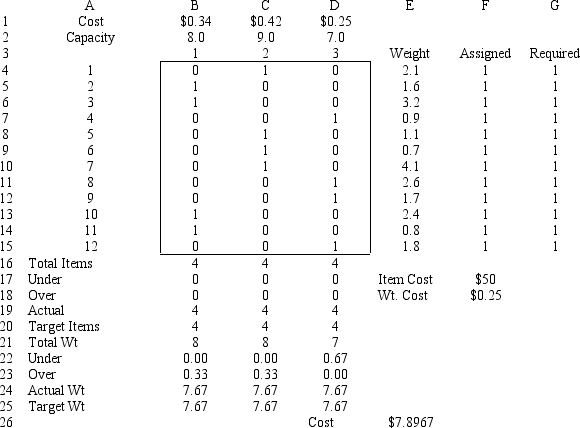
Refer to Exhibit 7.4. What formulas should go in cell E26 of the spreadsheet?
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
 Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Refer to Exhibit 7.4. What formulas should go in cell E26 of the spreadsheet?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
42
A company makes 2 products A and B from 2 resources. The products have the following resource requirements and produce the accompanying profits. The available quantity of resources is also shown in the table. 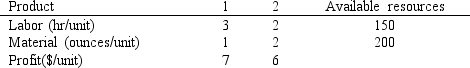 Management has developed the following set of goals
Management has developed the following set of goals
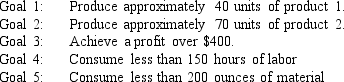 Based on the following GP formulation of the problem, and the associated optimal solution, what formulas should go in cells D6:F6, B9:F9, and B16 of the following Excel spreadsheet? NOTE: Formulas are not required in all of these cells.
Based on the following GP formulation of the problem, and the associated optimal solution, what formulas should go in cells D6:F6, B9:F9, and B16 of the following Excel spreadsheet? NOTE: Formulas are not required in all of these cells.
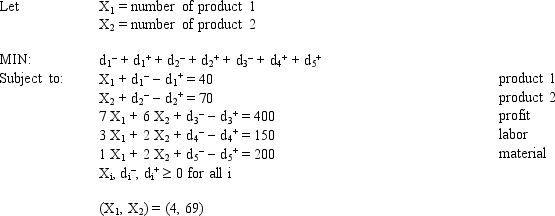
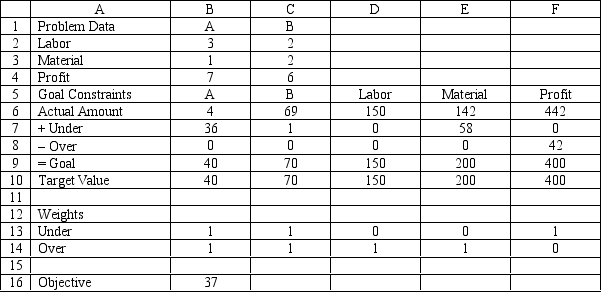
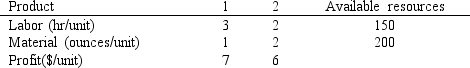 Management has developed the following set of goals
Management has developed the following set of goals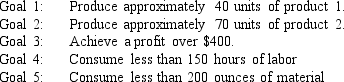 Based on the following GP formulation of the problem, and the associated optimal solution, what formulas should go in cells D6:F6, B9:F9, and B16 of the following Excel spreadsheet? NOTE: Formulas are not required in all of these cells.
Based on the following GP formulation of the problem, and the associated optimal solution, what formulas should go in cells D6:F6, B9:F9, and B16 of the following Excel spreadsheet? NOTE: Formulas are not required in all of these cells.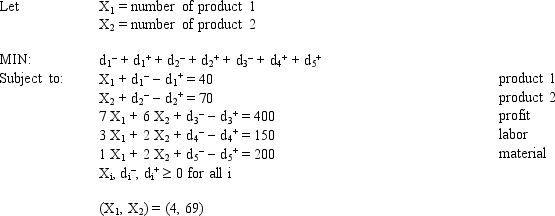


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.

Refer to Exhibit 7.4. Based on the integer goal programming formulation, the associated solution, and spreadsheet model, what formulas should go in cells B19:E19 and B24:E24 of the spreadsheet?
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
 Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Refer to Exhibit 7.4. Based on the integer goal programming formulation, the associated solution, and spreadsheet model, what formulas should go in cells B19:E19 and B24:E24 of the spreadsheet?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
44
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
The following Excel spreadsheet has been created to solve a goal programming problem with a MINIMAX objective based on the following goal programming formulation with MINIMAX objective and corresponding solution.
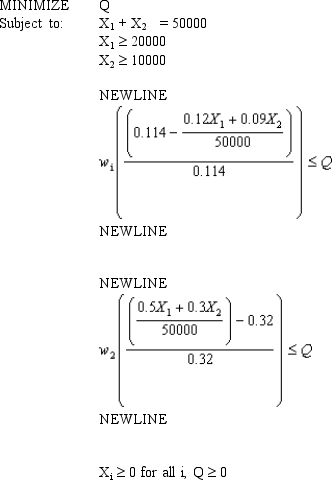 with solution (X1, X2) = (15,370, 34,630).
with solution (X1, X2) = (15,370, 34,630).
What values should go in cells B2:D14 of the spreadsheet?
 Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.The following Excel spreadsheet has been created to solve a goal programming problem with a MINIMAX objective based on the following goal programming formulation with MINIMAX objective and corresponding solution.
 with solution (X1, X2) = (15,370, 34,630).
with solution (X1, X2) = (15,370, 34,630).What values should go in cells B2:D14 of the spreadsheet?


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
45
A company makes 2 products A and B from 2 resources, labor and material. The products have the following resource requirements and produce the accompanying profits. The available quantity of resources is also shown in the table.  Management has developed the following set of goals
Management has developed the following set of goals
 Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.
 Management has developed the following set of goals
Management has developed the following set of goals Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
46
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.

Refer to Exhibit 7.4. Given the solution indicated in the spreadsheet, which trucks, if any, are under an equal weight amount, and which trucks are over an equal weight amount?
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
 Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Refer to Exhibit 7.4. Given the solution indicated in the spreadsheet, which trucks, if any, are under an equal weight amount, and which trucks are over an equal weight amount?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
47
A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000.
Based on the following formulation and associated integer solution, what values should go in cells B2:E16 of the spreadsheet?
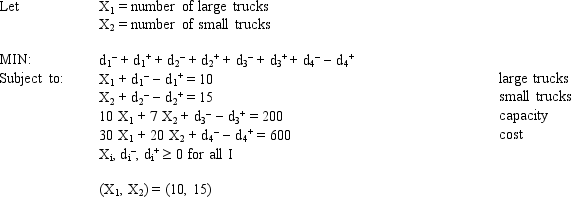

Based on the following formulation and associated integer solution, what values should go in cells B2:E16 of the spreadsheet?
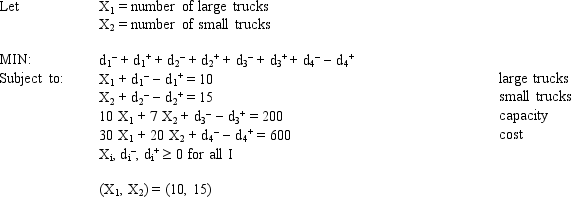


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
48
A dietician wants to formulate a low cost, high calorie food product for a customer. The following information is available about the 2 ingredients which can be combined to make the food. The customer wants 1000 pounds of the food product and it must contain at least 250 pounds of Food 1 and 300 pounds of Food 2.
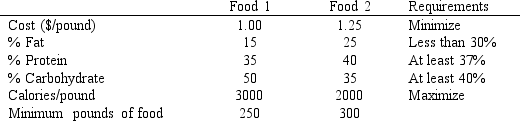 Formulate the MOLP for this problem.
Formulate the MOLP for this problem.
 Formulate the MOLP for this problem.
Formulate the MOLP for this problem.
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
49
A company makes 2 products A and B from 2 resources. The products have the following resource requirements and produce the accompanying profits. The available quantity of resources is also shown in the table. 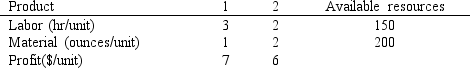 Management has developed the following set of goals
Management has developed the following set of goals
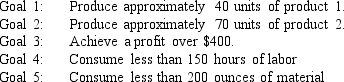 Based on this GP formulation of the problem and the associated optimal integer solution what values should go in cells B2:F16 of the following Excel spreadsheet?
Based on this GP formulation of the problem and the associated optimal integer solution what values should go in cells B2:F16 of the following Excel spreadsheet?
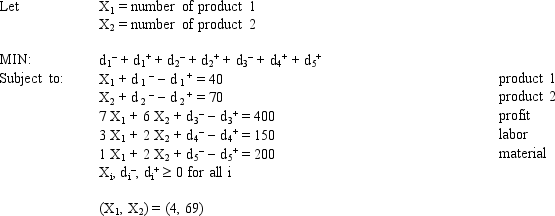
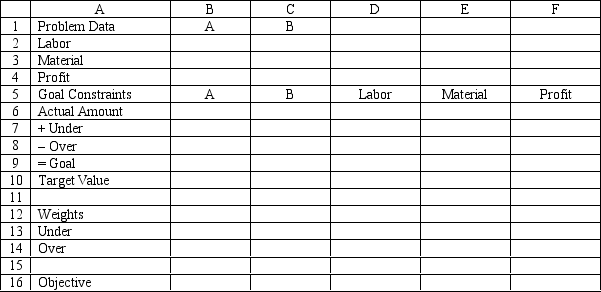
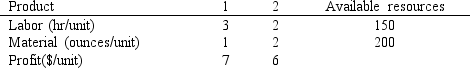 Management has developed the following set of goals
Management has developed the following set of goals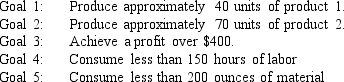 Based on this GP formulation of the problem and the associated optimal integer solution what values should go in cells B2:F16 of the following Excel spreadsheet?
Based on this GP formulation of the problem and the associated optimal integer solution what values should go in cells B2:F16 of the following Excel spreadsheet?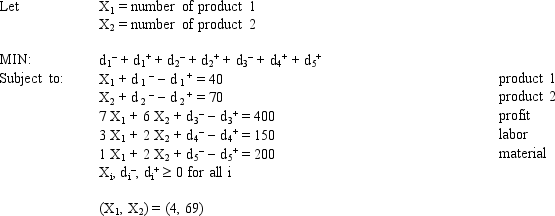


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
50
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
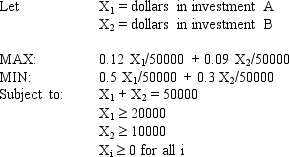 The solution for the second LP is (X1, X2) = (20,000, 30,000).
The solution for the second LP is (X1, X2) = (20,000, 30,000).
What formulas should go in cells B2:D11 of the spreadsheet? NOTE: Formulas are not required in all of these cells.
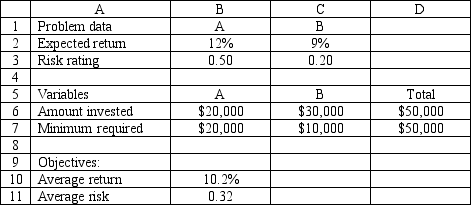
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem: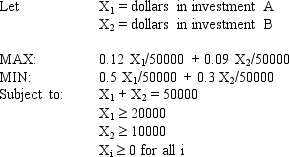 The solution for the second LP is (X1, X2) = (20,000, 30,000).
The solution for the second LP is (X1, X2) = (20,000, 30,000).What formulas should go in cells B2:D11 of the spreadsheet? NOTE: Formulas are not required in all of these cells.


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.

Refer to Exhibit 7.4. The solution indicates Truck 3 is under the target weight by 67 pounds. What if anything can be done to this model to provide a solution in which Truck 3 is closer to the target weight?
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
 Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Refer to Exhibit 7.4. The solution indicates Truck 3 is under the target weight by 67 pounds. What if anything can be done to this model to provide a solution in which Truck 3 is closer to the target weight?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
52
A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000.
Based on the following goal programming formulation, associated solution, and spreadsheet model, what formulas should go in cells D6:E6, B9:E9, and B16 of the spreadsheet?
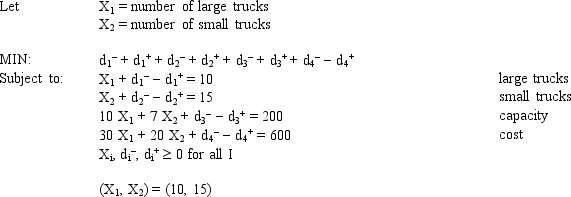
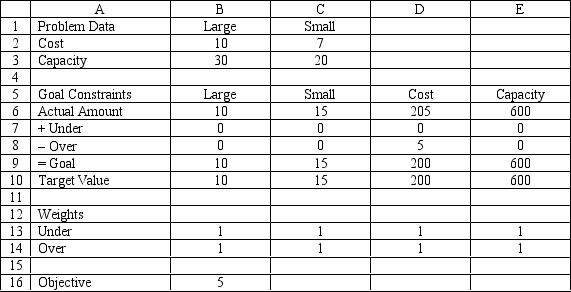
Based on the following goal programming formulation, associated solution, and spreadsheet model, what formulas should go in cells D6:E6, B9:E9, and B16 of the spreadsheet?
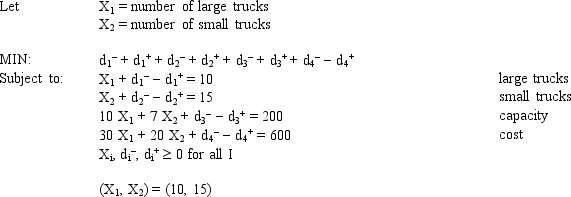


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
53
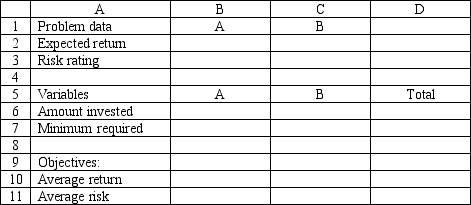
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
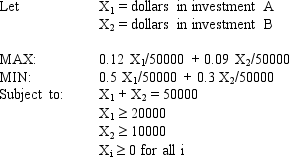 The solution for the second LP is (X1, X2) = (20,000, 30,000).
The solution for the second LP is (X1, X2) = (20,000, 30,000).
Based on this solution, what values should go in cells B2:D11 of the spreadsheet?
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem: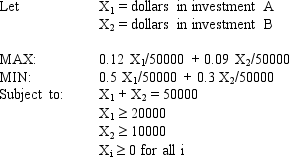 The solution for the second LP is (X1, X2) = (20,000, 30,000).
The solution for the second LP is (X1, X2) = (20,000, 30,000).Based on this solution, what values should go in cells B2:D11 of the spreadsheet?


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
54
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j. Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.

Refer to Exhibit 7.4. The spreadsheet model has scaled all the weights from pounds into 100s pounds. How does this scaling effect the solution obtained using the Risk Solver Platform (RSP)?
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
 Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Refer to Exhibit 7.4. The spreadsheet model has scaled all the weights from pounds into 100s pounds. How does this scaling effect the solution obtained using the Risk Solver Platform (RSP)?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
55
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.Formulate the MOLP for this investor.
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.Formulate the MOLP for this investor.
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.Formulate the MOLP for this investor.
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.Formulate the MOLP for this investor.
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
56
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Formulate the integer goal programming problem for Robert. (Hint: objective function involves decision and deviation variables.)
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.Formulate the integer goal programming problem for Robert. (Hint: objective function involves decision and deviation variables.)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
57
A dietician wants to formulate a low cost, high calorie food product for a customer. The following information is available about the 2 ingredients which can be combined to make the food. The customer wants 1000 pounds of the food product and it should contain 250 pounds of Food 1 and 300 pounds of Food 2. The final cost of the blend should be about $1.15 and contain about 2500 calories per pound. The percent of fat, protein, carbohydrate in each food is summarized below with the target values for the goals. The dietician would prefer the food product be low in fat while also high in protein and carbohydrates.
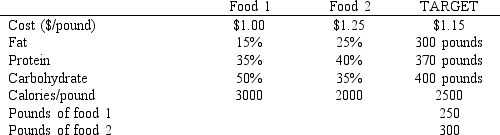 Formulate the GP for this problem
Formulate the GP for this problem
 Formulate the GP for this problem
Formulate the GP for this problem
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
58
A company needs to supply customers in 3 cities from its 3 warehouses. The supplies, demands and shipping costs are shown below.
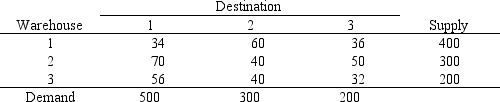 The company has identified the following goals:
The company has identified the following goals:
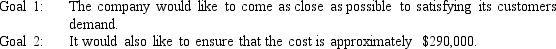 Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.
 The company has identified the following goals:
The company has identified the following goals: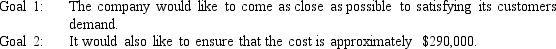 Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
59
A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000.
Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
60
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Formulate a goal programming model with a MINIMAX objective function.
 Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.Formulate a goal programming model with a MINIMAX objective function.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
61
You have been hired by the city of Twin Rivers to conduct analyses in support of their "Care for our Children" program.
The city council of Twin Rivers recently passed a resolution to fund much needed child care facilities for the city. A total of $850,000 has been made available to buy or lease child care sites throughout the city. An initial survey of the requirements for city-supported facilities has already been conducted and that data will form the basis of the siting and facility selection analysis process. That initial survey indicated the need for facilities providing four categories of child care: infant care, pre-school care, after school care, and drop-in care. The survey indicated the following minimum requirements for each category of child care. Naturally, a goal of this program is not only to try and cover these minimum requirements, but also to try and maximize the total number of child care slots created.

Various sites have been identified and these sites are either for lease or for sale. The leased sites require no additional modification at city expense. All modification expenses are borne by the owner. The sites for sale will require some level of renovation and these renovation costs have been rolled into the purchase cost for the site. Additionally, some types of maintenance on leased sites will be borne by the owner reducing the expected maintenance costs the city must cover. The sites and the pertinent information about those sites is summarized in the table below. Note that all costs are in $1000s. Each site was also assessed regarding the relative "safety" of the site. Safety issues included such things as parking, condition of the grounds, and condition of the structure. A safety index was used with each site rated as 1 for acceptably safe, 2 for marginally safe, and 3 for marginally safe given some modifications. Any sites surveyed found unacceptable in the safety department were dropped from further consideration.
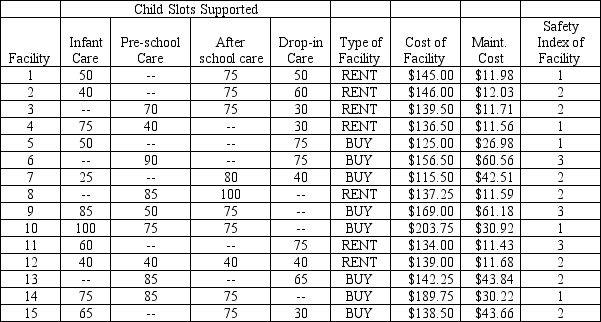
These new facilities will require staffing. The city council would like insight into the number of new staff required and the subsequent annual personnel budget to accommodate these new positions. Medical, administration, and of course providers are required for the facilities. The desired level of staffing is based on a projected child-to-staff ratio. For planning purposes, a Created Slot-to-Staff ratio can be employed.
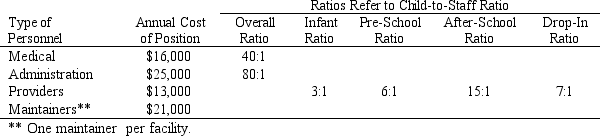
Although the city council has agreed to fund this project for approximately $850,000, reasonable targets for maintenance and personnel costs, and safety index levels must be established. The city council members would not only like recommendations on site selection that account for all the goals established for this project, they would like a summary breakout of the personnel requirements and costs associated with the recommended options.
Requirements:
a. Formulate the MOLP appropriate for this problem.
b. Implement and solve the MOLP using the Risk Solver Platform (RSP).
c. Formulate the GP appropriate for this problem.
d. Implement and solve the GP using the Risk Solver Platform (RSP).
e. Report your initial recommendation and a summary of the requirements for that recommendation.
f. Consider other issues that might arise in the current situation, adjust your model and report the results accordingly.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
62
Recent growth in the college's enrollment has been disproportional among her five primary departments. As a result, she is concerned about the mix of faculty and staff within each of the departments. Her concerns have been echoed in some recent staff meetings involving her department heads. This concern prompted a call to the consulting company you work for which in turn led to your assignment to investigate the Dean's problem.
Since the Dean feels the faculty mix and staff allocation is out-of-kilter across the departments, she would like an independent staffing analysis completed. She further wants this analysis completed "in the blind" with respect to her current staffing. Part of her rationale for this blind study concept is to avoid a rampant rumor mill suggesting a consulting was going to be cutting faculty and staff.Since Maxwell is primarily a teaching college, the teaching load among all the faculty is quite high. Naturally, the more senior in academic rank to receive some perks. The faculty teach courses both for students enrolled in their department's programs and to students enrolled in programs within other departments. These courses are referred to as In-Department and Out-Department courses, respectively. The number of In-Department and Out-Department courses per faculty member varies by academic rank and by the department. Within a department, the numbers are consistent among comparable faculty members.
The following data was provided by the Dean.
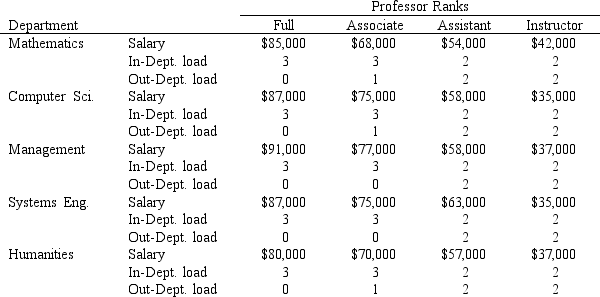 For the purposes of the study, the Dean suggested using an average of 3 classes per semester per student for In-Department course requirements and 2 classes per semester per student for Out-Department course requirements. The average class size is 20 students per class. For the purposes of the student, you may assume every department offers an equal share of the Out-Department course requirements across all five departments. Naturally, the Dean wants to ensure the staffing study suggests a faculty sufficient to handle to the expected number of courses offered.Through discussions with the Dean, various study goals became apparent and are listed below:
For the purposes of the study, the Dean suggested using an average of 3 classes per semester per student for In-Department course requirements and 2 classes per semester per student for Out-Department course requirements. The average class size is 20 students per class. For the purposes of the student, you may assume every department offers an equal share of the Out-Department course requirements across all five departments. Naturally, the Dean wants to ensure the staffing study suggests a faculty sufficient to handle to the expected number of courses offered.Through discussions with the Dean, various study goals became apparent and are listed below: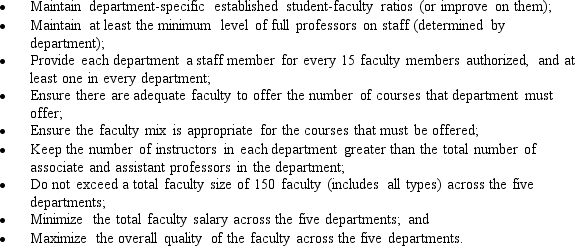
Additional data provided by the Dean pertinent to these goals is provided in the following table:
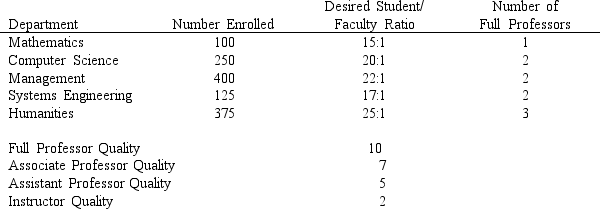
You have quickly realized that this is a multi-objective linear programming problem to find a solution that will minimize faculty salary costs and to find a solution to maximize the quality of a faculty mix. Since these are competing objectives, once determined, you will need to roll these values into a goal programming model to then interact with the Dean and arrive at a suitable faculty mix solution.
a. Formulate a MOLP for this problem.
b. Implement the MOLP in Excel and use the Risk Solver Platform (RSP) to find solutions. Report the suggested faculty and staff mix to obtain a minimum cost faculty, a maximum quality faculty, and the minimum size faculty required.c. Formulate the GP for this problem.
d. Implement the GP in Excel and solve the model using the Risk Solver Platform (RSP). Report back the suggested faculty and staff mix.
e. Examine the solution obtained in Part d. If any of the goals seem to far out of line, adjust your goal programming weights, resolve and re-examine the suggested solution.
a.Formulate a MOLP for this problem.
b.Implement the MOLP in Excel and use the Risk Solver Platform (RSP) to find solutions. Report the suggested faculty and staff mix to obtain a minimum cost faculty, a maximum quality faculty, and the minimum size faculty required.
c.Formulate the GP for this problem.
d.Implement the GP in Excel and solve the model using the Risk Solver Platform (RSP). Report back the suggested faculty and staff mix.
d. If any of the goals seem to far out of line, adjust your goal programming weights, resolve and re-examine the suggested solution.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck


