Exam 7: Goal Programming and Multiple Objective Optimization
Exam 1: Introduction to Modeling and Decision Analysis51 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet89 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling73 Questions
Exam 6: Integer Linear Programming73 Questions
Exam 7: Goal Programming and Multiple Objective Optimization62 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis77 Questions
Exam 10: Discriminant Analysis60 Questions
Exam 11: Time Series Forecasting116 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory80 Questions
Exam 14: Decision Analysis101 Questions
Exam 15: Project Management Online63 Questions
Select questions type
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.
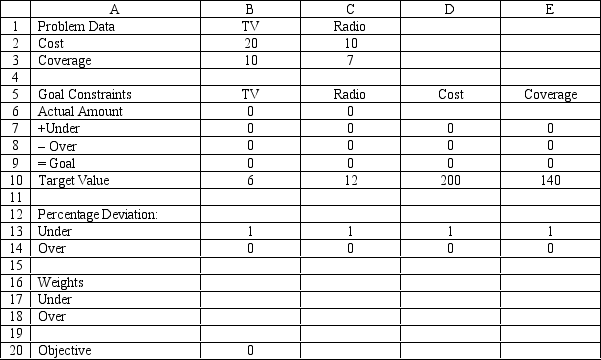 -Refer to Exhibit 7.1. Which of the following is a constraint specified to Risk Solver Platform (RSP) for this model?
-Refer to Exhibit 7.1. Which of the following is a constraint specified to Risk Solver Platform (RSP) for this model?
Free
(Multiple Choice)
5.0/5  (37)
(37)
Correct Answer:
C
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.  Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
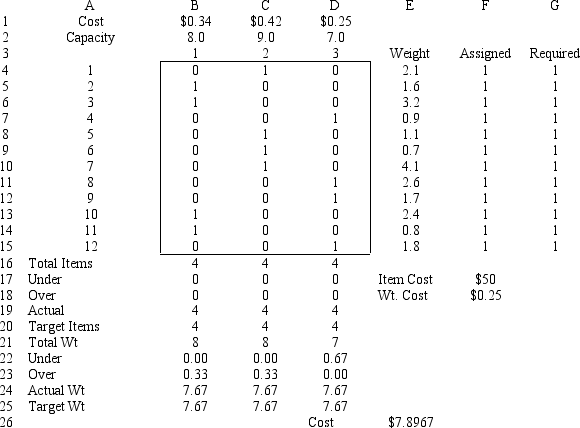 -Refer to Exhibit 7.4. The spreadsheet model has scaled all the weights from pounds into 100s pounds. How does this scaling effect the solution obtained using the Risk Solver Platform (RSP)?
-Refer to Exhibit 7.4. The spreadsheet model has scaled all the weights from pounds into 100s pounds. How does this scaling effect the solution obtained using the Risk Solver Platform (RSP)?
Free
(Essay)
4.7/5  (36)
(36)
Correct Answer:
The solution obtained is the same regardless of scaling. In terms of pounds, the total cost would be multiplied by 100, to obtain $78,967.
The di+, di- variables are referred to as
Free
(Multiple Choice)
4.9/5  (28)
(28)
Correct Answer:
D
What weight would be assigned to a neutral deviational variable?
(Multiple Choice)
4.8/5  (36)
(36)
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.
 -Refer to Exhibit 7.1. Which cells are the variable cells in this model?
-Refer to Exhibit 7.1. Which cells are the variable cells in this model?
(Multiple Choice)
4.9/5  (27)
(27)
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
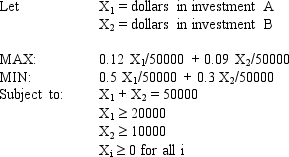 The solution for the second LP is (X1, X2) = (20,000, 30,000).
Based on this solution, what values should go in cells B2:D11 of the spreadsheet?
The solution for the second LP is (X1, X2) = (20,000, 30,000).
Based on this solution, what values should go in cells B2:D11 of the spreadsheet?
(Essay)
4.9/5  (37)
(37)
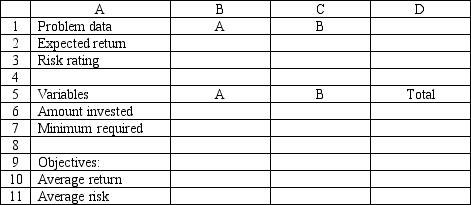
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
Note that a low Risk rating means a less risky investment. The investor can invest to maximize the expected rate of return or minimize risk. Any money beyond the minimum investment requirements can be invested in either fund.The following is the MOLP formulation for this problem:
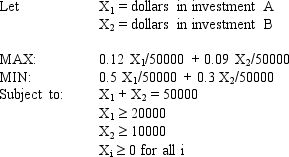 The solution for the second LP is (X1, X2) = (20,000, 30,000).
What formulas should go in cells B2:D11 of the spreadsheet? NOTE: Formulas are not required in all of these cells.
The solution for the second LP is (X1, X2) = (20,000, 30,000).
What formulas should go in cells B2:D11 of the spreadsheet? NOTE: Formulas are not required in all of these cells.
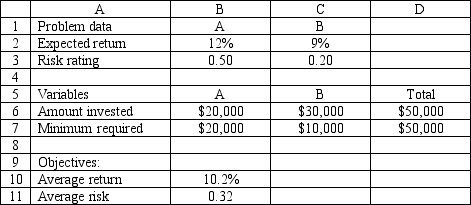
(Essay)
4.9/5  (34)
(34)
Which of the following are true regarding weights assigned to deviational variables?
(Multiple Choice)
4.9/5  (39)
(39)
You have been hired by the city of Twin Rivers to conduct analyses in support of their "Care for our Children" program.
The city council of Twin Rivers recently passed a resolution to fund much needed child care facilities for the city. A total of $850,000 has been made available to buy or lease child care sites throughout the city. An initial survey of the requirements for city-supported facilities has already been conducted and that data will form the basis of the siting and facility selection analysis process. That initial survey indicated the need for facilities providing four categories of child care: infant care, pre-school care, after school care, and drop-in care. The survey indicated the following minimum requirements for each category of child care. Naturally, a goal of this program is not only to try and cover these minimum requirements, but also to try and maximize the total number of child care slots created.
 Various sites have been identified and these sites are either for lease or for sale. The leased sites require no additional modification at city expense. All modification expenses are borne by the owner. The sites for sale will require some level of renovation and these renovation costs have been rolled into the purchase cost for the site. Additionally, some types of maintenance on leased sites will be borne by the owner reducing the expected maintenance costs the city must cover. The sites and the pertinent information about those sites is summarized in the table below. Note that all costs are in $1000s. Each site was also assessed regarding the relative "safety" of the site. Safety issues included such things as parking, condition of the grounds, and condition of the structure. A safety index was used with each site rated as 1 for acceptably safe, 2 for marginally safe, and 3 for marginally safe given some modifications. Any sites surveyed found unacceptable in the safety department were dropped from further consideration.
Various sites have been identified and these sites are either for lease or for sale. The leased sites require no additional modification at city expense. All modification expenses are borne by the owner. The sites for sale will require some level of renovation and these renovation costs have been rolled into the purchase cost for the site. Additionally, some types of maintenance on leased sites will be borne by the owner reducing the expected maintenance costs the city must cover. The sites and the pertinent information about those sites is summarized in the table below. Note that all costs are in $1000s. Each site was also assessed regarding the relative "safety" of the site. Safety issues included such things as parking, condition of the grounds, and condition of the structure. A safety index was used with each site rated as 1 for acceptably safe, 2 for marginally safe, and 3 for marginally safe given some modifications. Any sites surveyed found unacceptable in the safety department were dropped from further consideration.
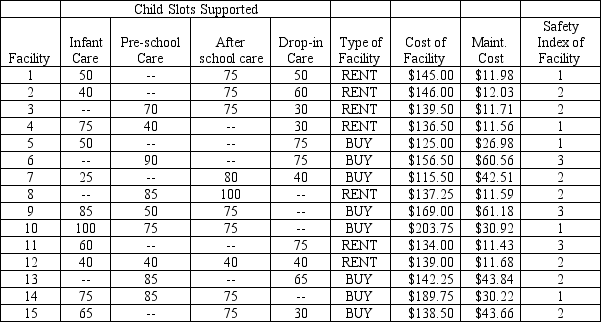 These new facilities will require staffing. The city council would like insight into the number of new staff required and the subsequent annual personnel budget to accommodate these new positions. Medical, administration, and of course providers are required for the facilities. The desired level of staffing is based on a projected child-to-staff ratio. For planning purposes, a Created Slot-to-Staff ratio can be employed.
These new facilities will require staffing. The city council would like insight into the number of new staff required and the subsequent annual personnel budget to accommodate these new positions. Medical, administration, and of course providers are required for the facilities. The desired level of staffing is based on a projected child-to-staff ratio. For planning purposes, a Created Slot-to-Staff ratio can be employed. 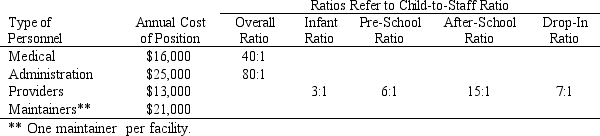 Although the city council has agreed to fund this project for approximately $850,000, reasonable targets for maintenance and personnel costs, and safety index levels must be established. The city council members would not only like recommendations on site selection that account for all the goals established for this project, they would like a summary breakout of the personnel requirements and costs associated with the recommended options.
Requirements:
a. Formulate the MOLP appropriate for this problem.
b. Implement and solve the MOLP using the Risk Solver Platform (RSP).
c. Formulate the GP appropriate for this problem.
d. Implement and solve the GP using the Risk Solver Platform (RSP).
e. Report your initial recommendation and a summary of the requirements for that recommendation.
f. Consider other issues that might arise in the current situation, adjust your model and report the results accordingly.
Although the city council has agreed to fund this project for approximately $850,000, reasonable targets for maintenance and personnel costs, and safety index levels must be established. The city council members would not only like recommendations on site selection that account for all the goals established for this project, they would like a summary breakout of the personnel requirements and costs associated with the recommended options.
Requirements:
a. Formulate the MOLP appropriate for this problem.
b. Implement and solve the MOLP using the Risk Solver Platform (RSP).
c. Formulate the GP appropriate for this problem.
d. Implement and solve the GP using the Risk Solver Platform (RSP).
e. Report your initial recommendation and a summary of the requirements for that recommendation.
f. Consider other issues that might arise in the current situation, adjust your model and report the results accordingly.
(Essay)
4.8/5  (33)
(33)
An investor wants to invest $50,000 in two mutual funds, A and B. The rates of return, risks and minimum investment requirements for each fund are:
 Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Formulate a goal programming model with a MINIMAX objective function.
Note that a low Risk rating means a less risky investment. The investor wants to maximize the expected rate of return while minimizing his risk. Any money beyond the minimum investment requirements can be invested in either fund. The investor has found that the maximum possible expected rate of return is 11.4% and the minimum possible risk is 0.32.
Formulate a goal programming model with a MINIMAX objective function.
(Essay)
4.9/5  (37)
(37)
Suppose that the first goal in a GP problem is to make 3 X1 + 4 X2 approximately equal to 36. Using the deviational variables d1- and d1+, what constraint can be used to express this goal?
(Multiple Choice)
4.8/5  (30)
(30)
If no other feasible solution to a multi-objective linear programming (MOLP) problem allows an increase in any objective without decreasing at least one other objective, the solution is said to be
(Multiple Choice)
4.8/5  (32)
(32)
An optimization technique useful for solving problems with more than one objective function is
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.  Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
 -Refer to Exhibit 7.4. The solution indicates Truck 3 is under the target weight by 67 pounds. What if anything can be done to this model to provide a solution in which Truck 3 is closer to the target weight?
-Refer to Exhibit 7.4. The solution indicates Truck 3 is under the target weight by 67 pounds. What if anything can be done to this model to provide a solution in which Truck 3 is closer to the target weight?
(Essay)
4.9/5  (31)
(31)
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.
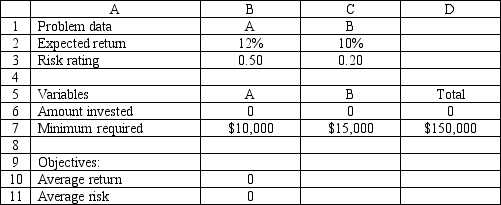 -Refer to Exhibit 7.2. What formula goes in cell B11?
-Refer to Exhibit 7.2. What formula goes in cell B11?
(Multiple Choice)
4.8/5  (30)
(30)
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.
 -Refer to Exhibit 7.2. What formula goes in cell B10?
-Refer to Exhibit 7.2. What formula goes in cell B10?
(Multiple Choice)
4.9/5  (29)
(29)
A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000.
Based on the following formulation and associated integer solution, what values should go in cells B2:E16 of the spreadsheet?
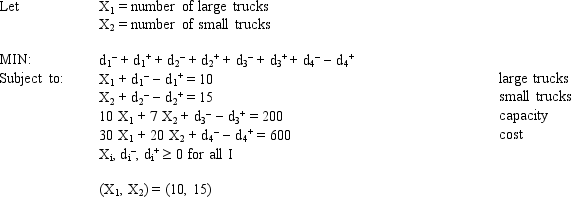
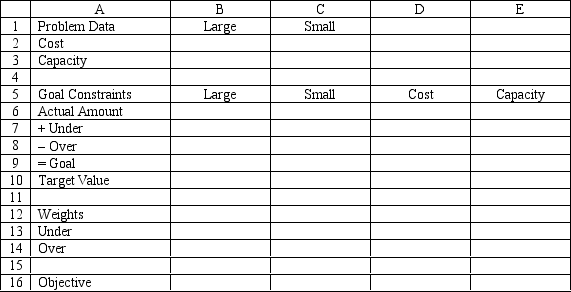
(Essay)
4.9/5  (39)
(39)
Which of the following is false regarding a goal constraint?
(Multiple Choice)
4.9/5  (39)
(39)
Recent growth in the college's enrollment has been disproportional among her five primary departments. As a result, she is concerned about the mix of faculty and staff within each of the departments. Her concerns have been echoed in some recent staff meetings involving her department heads. This concern prompted a call to the consulting company you work for which in turn led to your assignment to investigate the Dean's problem.
Since the Dean feels the faculty mix and staff allocation is out-of-kilter across the departments, she would like an independent staffing analysis completed. She further wants this analysis completed "in the blind" with respect to her current staffing. Part of her rationale for this blind study concept is to avoid a rampant rumor mill suggesting a consulting was going to be cutting faculty and staff.Since Maxwell is primarily a teaching college, the teaching load among all the faculty is quite high. Naturally, the more senior in academic rank to receive some perks. The faculty teach courses both for students enrolled in their department's programs and to students enrolled in programs within other departments. These courses are referred to as In-Department and Out-Department courses, respectively. The number of In-Department and Out-Department courses per faculty member varies by academic rank and by the department. Within a department, the numbers are consistent among comparable faculty members.
The following data was provided by the Dean.
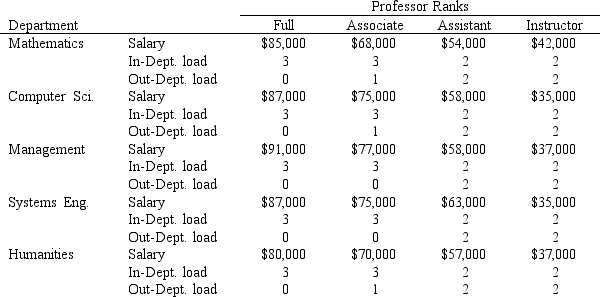 For the purposes of the study, the Dean suggested using an average of 3 classes per semester per student for In-Department course requirements and 2 classes per semester per student for Out-Department course requirements. The average class size is 20 students per class. For the purposes of the student, you may assume every department offers an equal share of the Out-Department course requirements across all five departments. Naturally, the Dean wants to ensure the staffing study suggests a faculty sufficient to handle to the expected number of courses offered.Through discussions with the Dean, various study goals became apparent and are listed below:
For the purposes of the study, the Dean suggested using an average of 3 classes per semester per student for In-Department course requirements and 2 classes per semester per student for Out-Department course requirements. The average class size is 20 students per class. For the purposes of the student, you may assume every department offers an equal share of the Out-Department course requirements across all five departments. Naturally, the Dean wants to ensure the staffing study suggests a faculty sufficient to handle to the expected number of courses offered.Through discussions with the Dean, various study goals became apparent and are listed below:
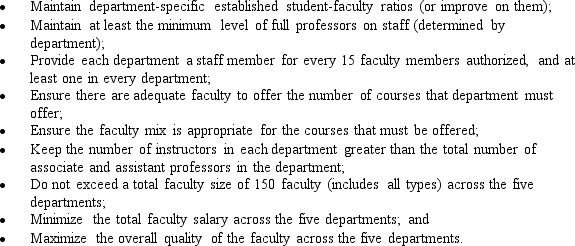 Additional data provided by the Dean pertinent to these goals is provided in the following table:
Additional data provided by the Dean pertinent to these goals is provided in the following table:
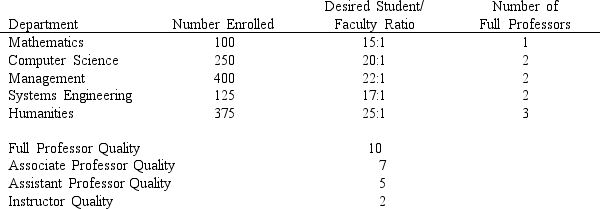 You have quickly realized that this is a multi-objective linear programming problem to find a solution that will minimize faculty salary costs and to find a solution to maximize the quality of a faculty mix. Since these are competing objectives, once determined, you will need to roll these values into a goal programming model to then interact with the Dean and arrive at a suitable faculty mix solution.
a. Formulate a MOLP for this problem.
b. Implement the MOLP in Excel and use the Risk Solver Platform (RSP) to find solutions. Report the suggested faculty and staff mix to obtain a minimum cost faculty, a maximum quality faculty, and the minimum size faculty required.c. Formulate the GP for this problem.
d. Implement the GP in Excel and solve the model using the Risk Solver Platform (RSP). Report back the suggested faculty and staff mix.
e. Examine the solution obtained in Part d. If any of the goals seem to far out of line, adjust your goal programming weights, resolve and re-examine the suggested solution.
a.Formulate a MOLP for this problem.
b.Implement the MOLP in Excel and use the Risk Solver Platform (RSP) to find solutions. Report the suggested faculty and staff mix to obtain a minimum cost faculty, a maximum quality faculty, and the minimum size faculty required.
c.Formulate the GP for this problem.
d.Implement the GP in Excel and solve the model using the Risk Solver Platform (RSP). Report back the suggested faculty and staff mix.
d. If any of the goals seem to far out of line, adjust your goal programming weights, resolve and re-examine the suggested solution.
You have quickly realized that this is a multi-objective linear programming problem to find a solution that will minimize faculty salary costs and to find a solution to maximize the quality of a faculty mix. Since these are competing objectives, once determined, you will need to roll these values into a goal programming model to then interact with the Dean and arrive at a suitable faculty mix solution.
a. Formulate a MOLP for this problem.
b. Implement the MOLP in Excel and use the Risk Solver Platform (RSP) to find solutions. Report the suggested faculty and staff mix to obtain a minimum cost faculty, a maximum quality faculty, and the minimum size faculty required.c. Formulate the GP for this problem.
d. Implement the GP in Excel and solve the model using the Risk Solver Platform (RSP). Report back the suggested faculty and staff mix.
e. Examine the solution obtained in Part d. If any of the goals seem to far out of line, adjust your goal programming weights, resolve and re-examine the suggested solution.
a.Formulate a MOLP for this problem.
b.Implement the MOLP in Excel and use the Risk Solver Platform (RSP) to find solutions. Report the suggested faculty and staff mix to obtain a minimum cost faculty, a maximum quality faculty, and the minimum size faculty required.
c.Formulate the GP for this problem.
d.Implement the GP in Excel and solve the model using the Risk Solver Platform (RSP). Report back the suggested faculty and staff mix.
d. If any of the goals seem to far out of line, adjust your goal programming weights, resolve and re-examine the suggested solution.
(Essay)
4.7/5  (53)
(53)
Given the following goal constraints
5 X1 + 6 X2 + 7 X3 + d1-- d1+ = 87
3 X1 + X2 + 4 X3 + d2-- d2+ = 37
7 X1 + 3 X2 + 2 X3 + d3- -d3+ = 72
and solution (X1, X2, X3) = (7, 2, 5), what values do the deviational variables assume?
(Essay)
4.9/5  (28)
(28)
Showing 1 - 20 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)