Deck 4: Sensitivity Analysis and the Simplex Method
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/77
Play
Full screen (f)
Deck 4: Sensitivity Analysis and the Simplex Method
1
The allowable decrease for a constraint is
A)how many more units of resource to purchase to maximize profits.
B)the amount by which the resource can decrease given shadow price.
C)how much resource to use to get the optimal solution.
D)the amount by which constraint coefficient can increase without changing the final optimal value.
A)how many more units of resource to purchase to maximize profits.
B)the amount by which the resource can decrease given shadow price.
C)how much resource to use to get the optimal solution.
D)the amount by which constraint coefficient can increase without changing the final optimal value.
B
2
A binding greater than or equal to ≥)constraint in a minimization problem means that
A)the variable is up against an upper limit.
B)the minimum requirement for the constraint has just been met.
C)another constraint is limiting the solution.
D)the shadow price for the constraint will be positive.
A)the variable is up against an upper limit.
B)the minimum requirement for the constraint has just been met.
C)another constraint is limiting the solution.
D)the shadow price for the constraint will be positive.
B
3
The allowable increase for a constraint is
A)how many more units of resource to purchase to maximize profits.
B)the amount by which the resource can increase given shadow price.
C)how much resource to use to get the optimal solution.
D)the amount by which the constraint coefficient can increase without changing the final optimal value.
A)how many more units of resource to purchase to maximize profits.
B)the amount by which the resource can increase given shadow price.
C)how much resource to use to get the optimal solution.
D)the amount by which the constraint coefficient can increase without changing the final optimal value.
B
4
The allowable increase for a changing cell decision variable)is
A)how many more units to produce to maximize profits.
B)the amount by which the objective function coefficient can increase without changing the optimal solution.
C)how much to charge to get the optimal solution.
D)the amount by which constraint coefficient can increase without changing the optimal solution.
A)how many more units to produce to maximize profits.
B)the amount by which the objective function coefficient can increase without changing the optimal solution.
C)how much to charge to get the optimal solution.
D)the amount by which constraint coefficient can increase without changing the optimal solution.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
5
The slope of the level curve for the objective function value can be changed by
A)increasing the value of the decision variables.
B)doubling all the coefficients in the objective function.
C)increasing the right hand sides of constraints.
D)changing a coefficient in the objective function.
A)increasing the value of the decision variables.
B)doubling all the coefficients in the objective function.
C)increasing the right hand sides of constraints.
D)changing a coefficient in the objective function.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
6
The difference between the right-hand side RHS)values of the constraints and the final optimal)value assumed by the left-hand side LHS)formula for each constraint is called the slack and is found in the
A)Status report
B)Slack report
C)Results report
D)Cell Value report
A)Status report
B)Slack report
C)Results report
D)Cell Value report

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
7
A manager should consider how sensitive the model is to changes in all of the following except
A)differential coefficients.
B)objective function coefficients.
C)constraint coefficients.
D)right-hand side values for constraints.
A)differential coefficients.
B)objective function coefficients.
C)constraint coefficients.
D)right-hand side values for constraints.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
8
A binding less than or equal to ≤)constraint in a maximization problem means
A)that all of the resource represented by the constraint is consumed in the solution.
B)it is not a constraint that the level curve contacts.
C)another constraint is limiting the solution.
D)the requirement for the constraint has been exceeded.
A)that all of the resource represented by the constraint is consumed in the solution.
B)it is not a constraint that the level curve contacts.
C)another constraint is limiting the solution.
D)the requirement for the constraint has been exceeded.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
9
Meaningful Analytic Solver Platform ASP)sensitivity report headings can be defined
A)by adding cell notes to spreadsheet cells.
B)by using the Guess button in the Analytic Solver Platform ASP)dialog box.
C)by carefully labeling rows and columns in the spreadsheet model.
D)naming cells in the spreadsheet model.
A)by adding cell notes to spreadsheet cells.
B)by using the Guess button in the Analytic Solver Platform ASP)dialog box.
C)by carefully labeling rows and columns in the spreadsheet model.
D)naming cells in the spreadsheet model.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
10
Analytic Solver Platform provides all of the following reports except
A)Answer
B)Sensitivity
C)Cost performance
D)Limits
A)Answer
B)Sensitivity
C)Cost performance
D)Limits

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
11
The Cell Value column in the Solver Answer Report shows
A)which constraints are binding.
B)final optimal)value assumed by each constraint cell.
C)objective function values.
D)Right hand sides of constraints.
A)which constraints are binding.
B)final optimal)value assumed by each constraint cell.
C)objective function values.
D)Right hand sides of constraints.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
12
The sensitivity analysis provides information about which of the following?
A)the impact of a change to an objective function coefficient.
B)the impact of a change in a resource level.
C)the impact of adding simple upper or lower bounds on a decision variable.
D)all of these.
A)the impact of a change to an objective function coefficient.
B)the impact of a change in a resource level.
C)the impact of adding simple upper or lower bounds on a decision variable.
D)all of these.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following statements is false concerning either of the Allowable Increase and Allowable Decrease columns in the Sensitivity Report?
A)The values equate the decision variable profit to the cost of resources expended.
B)The values give the range over which a shadow price is accurate.
C)The values give the range over which an objective function coefficient can change without changing the optimal solution.
D)The values provide a means to recognize when alternate optimal solution exist.
A)The values equate the decision variable profit to the cost of resources expended.
B)The values give the range over which a shadow price is accurate.
C)The values give the range over which an objective function coefficient can change without changing the optimal solution.
D)The values provide a means to recognize when alternate optimal solution exist.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
14
Benefits of sensitivity analysis include all the following except:
A)provides a better picture of how solutions change as model factors change.
B)fosters managerial acceptance of the optimal solution.
C)overcomes management skepticism of optimal solutions.
D)answers potential managerial questions regarding the solution to an LP problem.
A)provides a better picture of how solutions change as model factors change.
B)fosters managerial acceptance of the optimal solution.
C)overcomes management skepticism of optimal solutions.
D)answers potential managerial questions regarding the solution to an LP problem.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
15
Analytic Solver Platform provides sensitivity analysis information on all of the following except the
A)range of values for objective function coefficients which do not change optimal solution.
B)impact on optimal objective function value of changes in constrained resources.
C)impact on optimal objective function value of changes in value of decision variables.
D)impact on right hand sides of changes in constraint coefficients.
A)range of values for objective function coefficients which do not change optimal solution.
B)impact on optimal objective function value of changes in constrained resources.
C)impact on optimal objective function value of changes in value of decision variables.
D)impact on right hand sides of changes in constraint coefficients.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
16
When performing sensitivity analysis,which of the following assumptions must apply?
A)All other coefficients remain constant.
B)Only right hand side changes really mean anything.
C)The X1 variable change is the most important.
D)The non-negativity assumption can be relaxed
A)All other coefficients remain constant.
B)Only right hand side changes really mean anything.
C)The X1 variable change is the most important.
D)The non-negativity assumption can be relaxed

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
17
The allowable decrease for a changing cell decision variable)is
A)the amount by which the constraint coefficient can decrease without changing final optimal solution.
B)an indication of how many more units to produce to maximize profits.
C)the amount by which objective function coefficient can decrease without changing the final optimal solution.
D)an indication of how much to charge to get the optimal solution.
A)the amount by which the constraint coefficient can decrease without changing final optimal solution.
B)an indication of how many more units to produce to maximize profits.
C)the amount by which objective function coefficient can decrease without changing the final optimal solution.
D)an indication of how much to charge to get the optimal solution.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
18
Binding constraints have
A)zero slack.
B)negative slack.
C)positive slack.
D)surplus resources.
A)zero slack.
B)negative slack.
C)positive slack.
D)surplus resources.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
19
The coefficients in an LP model cj,aij,bj)represent
A)random variables.
B)numeric constants.
C)random constants.
D)numeric variables.
A)random variables.
B)numeric constants.
C)random constants.
D)numeric variables.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
20
When a manager considers the effect of changes in an LP model's coefficients he/she is performing
A)a random analysis.
B)a coefficient analysis.
C)a sensitivity analysis.
D)a qualitative analysis.
A)a random analysis.
B)a coefficient analysis.
C)a sensitivity analysis.
D)a qualitative analysis.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
21
What is the value of the slack variable in the following constraint when X1 and X2 are nonbasic and only non- negativity is used as simple bounds?
X1 + X2 + S1 = 100
A)0
B)50
C)100
D)can't be determined from the given information
X1 + X2 + S1 = 100
A)0
B)50
C)100
D)can't be determined from the given information

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
22
Given an objective function value of 150 and a shadow price for resource 1 of 5,if 10 more units of resource 1 are added assuming the allowable increase is greater than 10),what is the impact on the objective function value?
A)increase of 50
B)increase of unknown amount
C)decrease of 50
D)increase of 10
A)increase of 50
B)increase of unknown amount
C)decrease of 50
D)increase of 10

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
23
When the allowable increase or allowable decrease for the objective function coefficient of one or more variables is zero it indicates in the absence of degeneracy)that
A)the problem is infeasible.
B)alternate optimal solutions exist.
C)there is only one optimal solution.
D)no optimal solution can be found.
A)the problem is infeasible.
B)alternate optimal solutions exist.
C)there is only one optimal solution.
D)no optimal solution can be found.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
24
When a solution is degenerate the shadow prices and their ranges
A)may be interpreted in the usual way but they may not be unique.
B)must be disregarded.
C)are always valid and unique.
D)are always understated
A)may be interpreted in the usual way but they may not be unique.
B)must be disregarded.
C)are always valid and unique.
D)are always understated

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
25
To convert ≤ constraints into = constraints the Simplex method adds what type of variable to the constraint?
A)slack
B)dummy
C)redundant
D)spreading
A)slack
B)dummy
C)redundant
D)spreading

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
26
How many basic variables are there in a linear programming model which has n variables and m constraints?
A)n
B)m
C)n + m
D)n − m
A)n
B)m
C)n + m
D)n − m

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
27
All of the following are true about a variable with a negative reduced cost in a maximization problem except
A)its objective function coefficient must increase by that amount in order to enter the basis.
B)it is at its simple lower bound.
C)it has surplus resources.
D)the objective function value will decrease by that value if the variable is increased by one unit.
A)its objective function coefficient must increase by that amount in order to enter the basis.
B)it is at its simple lower bound.
C)it has surplus resources.
D)the objective function value will decrease by that value if the variable is increased by one unit.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
28
The shadow price of a nonbinding constraint is
A)positive
B)zero
C)negative
D)indeterminate
A)positive
B)zero
C)negative
D)indeterminate

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
29
If the shadow price for a resource is 0 and 150 units of the resource are added what happens to the optimal solution?
A)increases by an unknown amount
B)increases more than 0 but less than 150
C)no change
D)decreases by an unknown amount
A)increases by an unknown amount
B)increases more than 0 but less than 150
C)no change
D)decreases by an unknown amount

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
30
What is the value of the objective function if X1 is set to 0 in the following Limits Report?
Adjustable Lower Target Upper Target
Cell Name Value Limit Result Limit Result
$B$4 Number to make: X1 80 0 800 79.99999999 3200
$C$4 Number to make: X2 20 0 2400 20 3200
A)80
B)800
C)2400
D)3200
Adjustable Lower Target Upper Target
Cell Name Value Limit Result Limit Result
$B$4 Number to make: X1 80 0 800 79.99999999 3200
$C$4 Number to make: X2 20 0 2400 20 3200
A)80
B)800
C)2400
D)3200

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
31
When a solution is degenerate the reduced costs for the changing cells
A)is always equal to zero.
B)may not be unique.
C)may be set to any value the manager needs.
D)is equal to infinity.
A)is always equal to zero.
B)may not be unique.
C)may be set to any value the manager needs.
D)is equal to infinity.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
32
The absolute value of the shadow price indicates the amount by which the objective function will be
A)improved if the corresponding constraint is loosened.
B)improved if the corresponding constraint is tightened.
C)made worse if the corresponding constraint is loosened.
D)improved if the corresponding constraint is unchanged.
A)improved if the corresponding constraint is loosened.
B)improved if the corresponding constraint is tightened.
C)made worse if the corresponding constraint is loosened.
D)improved if the corresponding constraint is unchanged.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
33
The reduced cost for a changing cell decision variable)is
A)the amount by which the objective function value changes if the variable is increased by one unit.
B)how many more units to product to maximize profits.
C)the per unit profits minus the per unit costs for that variable.
D)equal to zero for variables at their optimal values.
A)the amount by which the objective function value changes if the variable is increased by one unit.
B)how many more units to product to maximize profits.
C)the per unit profits minus the per unit costs for that variable.
D)equal to zero for variables at their optimal values.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
34
For a minimization problem,if a decision variable's final value is 0,and its reduced cost is negative,which of the following is true?
A)Alternate optimal solutions exist.
B)There is evidence of degeneracy.
C)No feasible solution was found.
D)The variable has a non-negativity constraint.
A)Alternate optimal solutions exist.
B)There is evidence of degeneracy.
C)No feasible solution was found.
D)The variable has a non-negativity constraint.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
35
If the allowable increase for a constraint is 100 and we add 110 units of the resource what happens to the objective function value?
A)increase of 100
B)increase of 110
C)decrease of 100
D)increases but by unknown amount
A)increase of 100
B)increase of 110
C)decrease of 100
D)increases but by unknown amount

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
36
The solution to an LP problem is degenerate if
A)the right hand sides of any of the constraints have an allowable increase or allowable decrease of zero.
B)the shadow prices of any of the constraints have an allowable increase or allowable decrease of infinity.
C)the objective coefficients of any of the variables have an allowable increase or allowable decrease of zero.
D)the shadow prices of any of the constraints have an allowable increase or allowable decrease of zero.
A)the right hand sides of any of the constraints have an allowable increase or allowable decrease of zero.
B)the shadow prices of any of the constraints have an allowable increase or allowable decrease of infinity.
C)the objective coefficients of any of the variables have an allowable increase or allowable decrease of zero.
D)the shadow prices of any of the constraints have an allowable increase or allowable decrease of zero.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
37
A change in the right hand side of a binding constraint may change all of the following except
A)optimal value of the decision variables
B)slack values
C)other right hand sides
D)objective function value
A)optimal value of the decision variables
B)slack values
C)other right hand sides
D)objective function value

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
38
A variable with a final value equal to its simple lower or upper bound and a reduced cost of zero indicates that
A)an alternate optimal solution exists.
B)an error in formulation has been made.
C)the right hand sides should be increased.
D)the objective function needs new coefficients.
A)an alternate optimal solution exists.
B)an error in formulation has been made.
C)the right hand sides should be increased.
D)the objective function needs new coefficients.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
39
A change in the right hand side of a constraint changes
A)the slope of the objective function
B)objective function coefficients
C)other right hand sides
D)the feasible region
A)the slope of the objective function
B)objective function coefficients
C)other right hand sides
D)the feasible region

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
40
If the shadow price for a resource is 0 and 150 units of the resource are added what happens to the objective function value?
A)increase of 150
B)increases more than 0 but less than 150
C)no change
D)increases but by an unknown amount
A)increase of 150
B)increases more than 0 but less than 150
C)no change
D)increases but by an unknown amount

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
41
The Simplex method uses which of the following values to determine if the objective function value can be improved?
A)shadow price
B)target value
C)reduced cost
D)basic cost
A)shadow price
B)target value
C)reduced cost
D)basic cost

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
42
Jones Furniture Company produces beds and desks for college students.The production process requires carpentry and varnishing.Each bed requires 6 hours of carpentry and 4 hour of varnishing.Each desk requires 4 hours of carpentry and 8 hours of varnishing.There are 36 hours of carpentry time and 40 hours of varnishing time available.Beds generate $30 of profit and desks generate $40 of profit.Demand for desks is limited so at most 8 will be produced.
How much can the price of Desks drop before it is no longer profitable to produce them? Base your response on the following Analytic Solver Platform sensitivity output.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ? 36 carpentry)
4 X1 + 8 X2 ? 40 varnishing)X2 ? 8 demand for X2)
X1,X2 ? 0
How much can the price of Desks drop before it is no longer profitable to produce them? Base your response on the following Analytic Solver Platform sensitivity output.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ? 36 carpentry)
4 X1 + 8 X2 ? 40 varnishing)X2 ? 8 demand for X2)
X1,X2 ? 0

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 4.2
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1 = weight assigned to homework W2 = weight assigned to the project W3 = weight assigned to the mid-term W4 = weight assigned to the final
MAX: 75W1 + 94W2 + 85W3 + 92W4
Subject to: W1 + W2 + W3 + W4 = 1
W3 + W4 ≤ 0.70 W3 + W4 ≥ 0.50 0.05 ≤ W1 ≤ 0.25
0.05 ≤ W2 ≤ 0.25
0.10 ≤ W3 ≤ 0.40
0.10 ≤ W4 ≤ 0.40
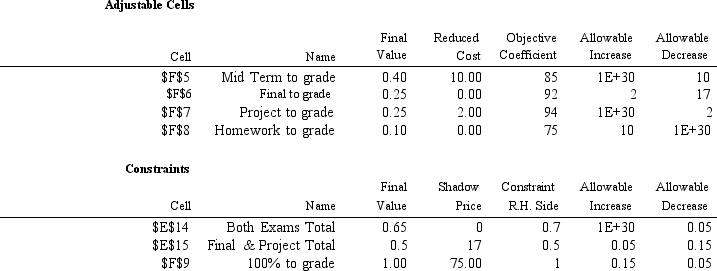
Refer to Exhibit 4.2.Constraint cell F9 corresponds to the constraint,W1 + W2 + W3 + W4 = 1,and has a shadow
price of 75.Armed with this information,what can Robert request of his instructor regarding this constraint?
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1 = weight assigned to homework W2 = weight assigned to the project W3 = weight assigned to the mid-term W4 = weight assigned to the final
MAX: 75W1 + 94W2 + 85W3 + 92W4
Subject to: W1 + W2 + W3 + W4 = 1
W3 + W4 ≤ 0.70 W3 + W4 ≥ 0.50 0.05 ≤ W1 ≤ 0.25
0.05 ≤ W2 ≤ 0.25
0.10 ≤ W3 ≤ 0.40
0.10 ≤ W4 ≤ 0.40

Refer to Exhibit 4.2.Constraint cell F9 corresponds to the constraint,W1 + W2 + W3 + W4 = 1,and has a shadow
price of 75.Armed with this information,what can Robert request of his instructor regarding this constraint?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
44
The optimization technique that locates solutions in the interior of the feasible region is known as
A)sub-optimal optimization
B)sensitivity analysis
C)robust optimization
D)USET optimization
A)sub-optimal optimization
B)sensitivity analysis
C)robust optimization
D)USET optimization

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
45
Exhibit 4.2
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1 = weight assigned to homework W2 = weight assigned to the project W3 = weight assigned to the mid-term W4 = weight assigned to the final
MAX: 75W1 + 94W2 + 85W3 + 92W4
Subject to: W1 + W2 + W3 + W4 = 1
W3 + W4 ≤ 0.70 W3 + W4 ≥ 0.50 0.05 ≤ W1 ≤ 0.25
0.05 ≤ W2 ≤ 0.25
0.10 ≤ W3 ≤ 0.40
0.10 ≤ W4 ≤ 0.40

Refer to Exhibit 4.2.Based on the Analytic Solver Platform sensitivity report information,is there anything Robert can request of his instructor to improve his final grade?
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1 = weight assigned to homework W2 = weight assigned to the project W3 = weight assigned to the mid-term W4 = weight assigned to the final
MAX: 75W1 + 94W2 + 85W3 + 92W4
Subject to: W1 + W2 + W3 + W4 = 1
W3 + W4 ≤ 0.70 W3 + W4 ≥ 0.50 0.05 ≤ W1 ≤ 0.25
0.05 ≤ W2 ≤ 0.25
0.10 ≤ W3 ≤ 0.40
0.10 ≤ W4 ≤ 0.40

Refer to Exhibit 4.2.Based on the Analytic Solver Platform sensitivity report information,is there anything Robert can request of his instructor to improve his final grade?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
46
The Simplex method works by first
A)identifying any basic feasible solution.
B)choosing the largest value for X1.
C)setting X1 at one-half of the its maximum value.
D)going directly to the optimal solution.
A)identifying any basic feasible solution.
B)choosing the largest value for X1.
C)setting X1 at one-half of the its maximum value.
D)going directly to the optimal solution.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
47
Exhibit 4.1
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j
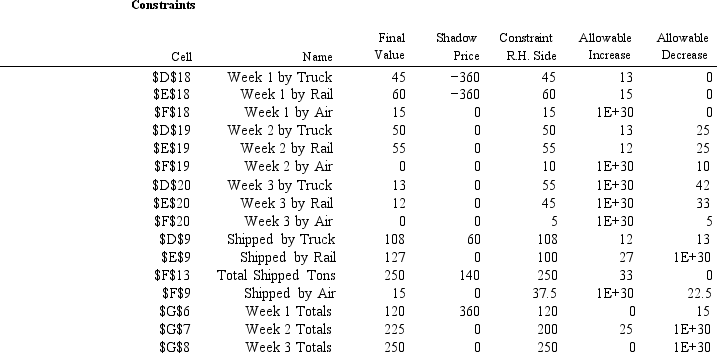
-Refer to Exhibit 4.1.The Week 1 by Truck and Week 1 by Rail constraints each have a shadow price of ?360.
What do these values imply?
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.The Week 1 by Truck and Week 1 by Rail constraints each have a shadow price of ?360.
What do these values imply?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
48
Why might a decision maker prefer a solution in the interior of the feasible region of a linear programming problem?
A)Such a solution has a better objective function value than any other solution
B)Such a solution is likely to remain feasible if some of the coefficients in the problem change
C)The decision maker is not sure if he/she wants to maximize or minimize the objective
D)Such a solution has more binding constraints
A)Such a solution has a better objective function value than any other solution
B)Such a solution is likely to remain feasible if some of the coefficients in the problem change
C)The decision maker is not sure if he/she wants to maximize or minimize the objective
D)Such a solution has more binding constraints

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
49
Exhibit 4.1
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.Of the three percentage of effort constraints,Shipped by Truck,Shipped by Rail,and Shipped by Air,which should be examined for potential cost reduction?
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.Of the three percentage of effort constraints,Shipped by Truck,Shipped by Rail,and Shipped by Air,which should be examined for potential cost reduction?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
50
Jones Furniture Company produces beds and desks for college students.The production process requires carpentry and varnishing.Each bed requires 6 hours of carpentry and 4 hour of varnishing.Each desk requires 4 hours of carpentry and 8 hours of varnishing.There are 36 hours of carpentry time and 40 hours of varnishing time available.Beds generate $30 of profit and desks generate $40 of profit.Demand for desks is limited so at most 8 will be produced.
Suppose the company can purchase more varnishing time for $3.00,should it be purchased and how much can be bought before the value of the additional time is uncertain? Base your response on the following Analytic Solver Platform sensitivity output.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ? 36 carpentry)
4 X1 + 8 X2 ? 40 varnishing)X2 ? 8 demand for X2)
X1,X2 ? 0
Suppose the company can purchase more varnishing time for $3.00,should it be purchased and how much can be bought before the value of the additional time is uncertain? Base your response on the following Analytic Solver Platform sensitivity output.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ? 36 carpentry)
4 X1 + 8 X2 ? 40 varnishing)X2 ? 8 demand for X2)
X1,X2 ? 0

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 4.1
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.Should the company negotiate for additional air delivery capacity?
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.Should the company negotiate for additional air delivery capacity?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
52
Is the optimal solution to this problem unique,or is there an alternate optimal solution? Explain your reasoning.
MAX 5 X1 + 2 X2
Subject to: 3 X1 + 5 X2 ≤ 15
10 X1 + 4 X2 ≤ 20 X1,X2 ≥ 0
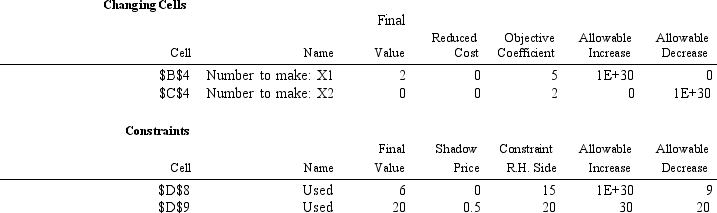
MAX 5 X1 + 2 X2
Subject to: 3 X1 + 5 X2 ≤ 15
10 X1 + 4 X2 ≤ 20 X1,X2 ≥ 0


Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
53
A solution to the system of equations using a set of basic variables is called
A)a feasible solution.
B)basic feasible solution.
C)a nonbasic solution.
D)a nonbasic feasible solution
A)a feasible solution.
B)basic feasible solution.
C)a nonbasic solution.
D)a nonbasic feasible solution

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
54
When automatically running multiple optimizations in Analytic Solver Platform,what spreadsheet function indicates which optimization is being run?
A)=PsiOptNum)
B)=PsiOptValue)
C)=PsiOptIndex)
D)=PsiCurrentOpt)
A)=PsiOptNum)
B)=PsiOptValue)
C)=PsiOptIndex)
D)=PsiCurrentOpt)

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
55
What are the objective function coefficients for X1 and X2 based on the following Analytic Solver Platform sensitivity output?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
56
What is the smallest value of the objective function coefficient X1 can assume without changing the optimal solution?
MAX: 7 X1 + 4 X2
Subject to: 2 X1 + X2 ≤ 16
X1 + X2 ≤ 10
2 X1 + 5 X2 ≤ 40 X1,X2 ≥ 0
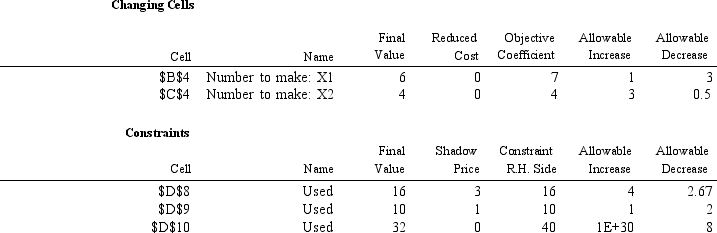
MAX: 7 X1 + 4 X2
Subject to: 2 X1 + X2 ≤ 16
X1 + X2 ≤ 10
2 X1 + 5 X2 ≤ 40 X1,X2 ≥ 0


Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
57
A farmer is planning his spring planting.He has 20 acres on which he can plant a combination of Corn,Pumpkins and Beans.He wants to maximize his profit but there is a limited demand for each crop.Each crop also requires fertilizer and irrigation water both of which are in short supply.The following table summarizes the data for the problem.
Based on the following Analytic Solver Platform sensitivity output,how much can the price of Corn drop before it is no longer profitable to plant corn?
Based on the following Analytic Solver Platform sensitivity output,how much can the price of Corn drop before it is no longer profitable to plant corn?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the following linear programming model and Analytic Solver Platform sensitivity output.What is the optimal objective function value if the RHS of the first constraint increases to 18?
MAX: 7 X1 + 4 X2
Subject to: 2 X1 + X2 ≤ 16
X1 + X2 ≤ 10
2 X1 + 5 X2 ≤ 40 X1,X2 ≥ 0
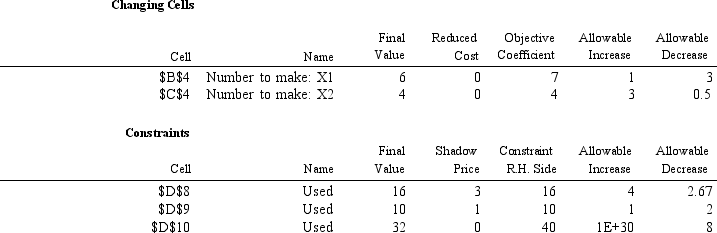
MAX: 7 X1 + 4 X2
Subject to: 2 X1 + X2 ≤ 16
X1 + X2 ≤ 10
2 X1 + 5 X2 ≤ 40 X1,X2 ≥ 0


Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
59
Exhibit 4.1
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.Are there alternate optimal solutions to this problem?
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
The following is the LP model for this logistics problem.
Let Xij = amount shipped by mode i in week j
where i = 1Truck),2Rail),3Air)and j = 1,2,3
Let WLij = weekly limit of mode i in week j as provided in above table)
200X11 + X12 + X13)+ 140X21 + X22 + X23)+ 500X31 +
MIN:
X + X )
Subject to:
32 33
Xij ? WL ij for all i and j Weekly limits by mode
X11 + X12 + X13 + X21 + X22 + X23 + X31 + X32 + X33 ? 250
Total at end of three weeks
X11 + X21 + X31 + X12 + X22 + X32 ? 200 Total at end of two weeks X11 + X21 + X31 ? 120 Total at end of first week
X11 + X12 + X13 ? 0.45*250 Truck mix requirement
X21 + X22 + X23 ? 0.40*250 Rail mix requirement
X31 + X32 + X33 ? 0.15*250 Air mix limit Xij ? 0 for all i and j

-Refer to Exhibit 4.1.Are there alternate optimal solutions to this problem?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
60
A farmer is planning his spring planting.He has 20 acres on which he can plant a combination of Corn,Pumpkins and Beans.He wants to maximize his profit but there is a limited demand for each crop.Each crop also requires fertilizer and irrigation water which are in short supply.The following table summarizes the data for the problem.
Suppose the farmer can purchase more fertilizer for $2.50 per pound,should he purchase it and how much can he buy and still be sure of the value of the additional fertilizer? Base your response on the following Analytic Solver Platform sensitivity output.
Suppose the farmer can purchase more fertilizer for $2.50 per pound,should he purchase it and how much can he buy and still be sure of the value of the additional fertilizer? Base your response on the following Analytic Solver Platform sensitivity output.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
61
A formulation has 20 variables and 8 constraints not counting non-negativity).How many variables are nonbasic?
A)8
B)12
C)20
D)28
A)8
B)12
C)20
D)28

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
62
Slack variables
A)are always equal to zero.
B)are usually negative.
C)are always positive.
D)can be positive or negative.
A)are always equal to zero.
B)are usually negative.
C)are always positive.
D)can be positive or negative.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
63
Finding a robust solution to an LP problem
A)is one of the many useful features of the Analytic Solver Platform
B)is trivial
C)is a guessing procedure
D)all of the above
A)is one of the many useful features of the Analytic Solver Platform
B)is trivial
C)is a guessing procedure
D)all of the above

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
64
A formulation has 10 variables and 4 constraints not counting non-negativity).How many variables are basic?
A)4
B)10
C)14
D)6
A)4
B)10
C)14
D)6

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the formulation below.How many decision variables will be there after the problem has been converted to a standard form?
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0
A)4
B)2
C)3
D)5
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0
A)4
B)2
C)3
D)5

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
66
When a variable is basic
A)it is present in the solution.
B)it may not be unique.
C)it is not present in the solution.
D)it's value is equal to zero.
A)it is present in the solution.
B)it may not be unique.
C)it is not present in the solution.
D)it's value is equal to zero.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
67
Solve this problem graphically.What is the optimal solution and what constraints are binding at the optimal solution?
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
68
Exhibit 4.2
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1 = weight assigned to homework W2 = weight assigned to the project W3 = weight assigned to the mid-term W4 = weight assigned to the final
MAX: 75W1 + 94W2 + 85W3 + 92W4
Subject to: W1 + W2 + W3 + W4 = 1
W3 + W4 ≤ 0.70 W3 + W4 ≥ 0.50 0.05 ≤ W1 ≤ 0.25
0.05 ≤ W2 ≤ 0.25
0.10 ≤ W3 ≤ 0.40
0.10 ≤ W4 ≤ 0.40

Refer to Exhibit 4.2.Based on the Analytic Solver Platform sensitivity report information,Robert has been approved by his instructor to increase the total weight allowed for the project and final exam to 0.50 plus the allowable increase.When Robert re-solves his model,what will his new final grade score be?
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1 = weight assigned to homework W2 = weight assigned to the project W3 = weight assigned to the mid-term W4 = weight assigned to the final
MAX: 75W1 + 94W2 + 85W3 + 92W4
Subject to: W1 + W2 + W3 + W4 = 1
W3 + W4 ≤ 0.70 W3 + W4 ≥ 0.50 0.05 ≤ W1 ≤ 0.25
0.05 ≤ W2 ≤ 0.25
0.10 ≤ W3 ≤ 0.40
0.10 ≤ W4 ≤ 0.40

Refer to Exhibit 4.2.Based on the Analytic Solver Platform sensitivity report information,Robert has been approved by his instructor to increase the total weight allowed for the project and final exam to 0.50 plus the allowable increase.When Robert re-solves his model,what will his new final grade score be?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
69
Solve this problem graphically.What is the optimal solution and what constraints are binding at the optimal solution?
MIN: 7 X1 + 3 X2
Subject to: 4 X1 + 4 X2 ≥ 40
2 X1 + 3 X2 ≥ 24 X1,X2 ≥ 0
MIN: 7 X1 + 3 X2
Subject to: 4 X1 + 4 X2 ≥ 40
2 X1 + 3 X2 ≥ 24 X1,X2 ≥ 0

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the formulation below.The standard form of the second constraint is:
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≥ 18
X1,X2 ≥ 0
A)5 X1 + 5 X2 = 20
B)6 X1 + 2 X2 = 18
C)6 X1 + 2 X2 + S2 = 18
D)6 X1 + 2 X2 - S2 = 18
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≥ 18
X1,X2 ≥ 0
A)5 X1 + 5 X2 = 20
B)6 X1 + 2 X2 = 18
C)6 X1 + 2 X2 + S2 = 18
D)6 X1 + 2 X2 - S2 = 18

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
71
A robust solution to an LP problem
A)is interior of the feasible region
B)has a reasonably good objective function value
C)is sub-optimal
D)all of the above
A)is interior of the feasible region
B)has a reasonably good objective function value
C)is sub-optimal
D)all of the above

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
72
Use slack variables to rewrite this problem so that all its constraints are equality constraints.
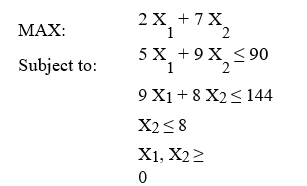
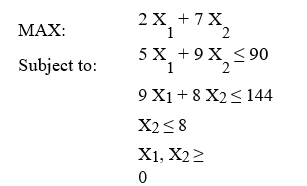

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
73
What needs to be done to the two constraints in order to convert the problem to a standard form?
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0
A)a slack variable needs to be added to each constraint to convert them to equalities.
B)nothing.
C)they need to be combined to a single constraint.
D)they need to be subtracted side-by-side
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0
A)a slack variable needs to be added to each constraint to convert them to equalities.
B)nothing.
C)they need to be combined to a single constraint.
D)they need to be subtracted side-by-side

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
74
The simplex method of linear programming LP):
A)moves to better and better corner point solution of the feasible region until no further objective function improvement can be achieved
B)explicitly enumerates all corner points of the feasible region and selects the best objective function value
C)evaluates all constraints for feasibility
D)does not cover all constraints to equalities
A)moves to better and better corner point solution of the feasible region until no further objective function improvement can be achieved
B)explicitly enumerates all corner points of the feasible region and selects the best objective function value
C)evaluates all constraints for feasibility
D)does not cover all constraints to equalities

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
75
A spider plot
A)is a graphical representation of multiple optimization runs
B)requires multiple runs of the problem
C)is computationally expensive to generate for problems with many constraints and variables
D)all of the above
A)is a graphical representation of multiple optimization runs
B)requires multiple runs of the problem
C)is computationally expensive to generate for problems with many constraints and variables
D)all of the above

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
76
Use slack variables to rewrite this problem so that all its constraints are equality constraints.
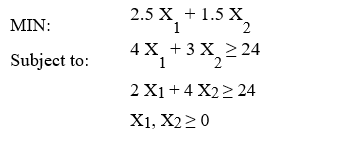
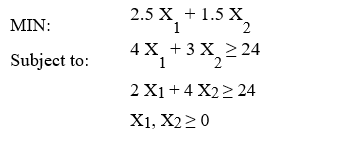

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
77
The simplex method of linear programming LP):
A)considers only the extreme points of the feasible region to achieve efficiency in solving LP problems
B)explicitly enumerates all corner points of the feasible region and selects the best objective function value
C)evaluates all constraints for feasibility
D)is not used in the Analytic Solver Platform software
A)considers only the extreme points of the feasible region to achieve efficiency in solving LP problems
B)explicitly enumerates all corner points of the feasible region and selects the best objective function value
C)evaluates all constraints for feasibility
D)is not used in the Analytic Solver Platform software

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck


