Deck 12: Extension E: Multiple Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/11
Play
Full screen (f)
Deck 12: Extension E: Multiple Integrals
1
Find the moment of inertia about the y-axis for a cube of constant density 3 and side length 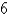 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.
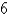 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.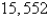
2
Find the mass of the solid S bounded by the paraboloid 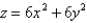 and the plane
and the plane 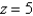 if S has constant density 3.
if S has constant density 3.
A) 15.07
B) 16.25
C) 24.91
D) 13.92
E) 19.63
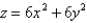 and the plane
and the plane 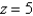 if S has constant density 3.
if S has constant density 3.A) 15.07
B) 16.25
C) 24.91
D) 13.92
E) 19.63
19.63
3
Use a triple integral to find the volume of the solid bounded by 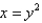 and the planes
and the planes 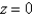 and
and 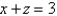
A)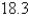
B)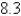
C)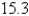
D)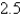
E)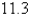
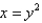 and the planes
and the planes 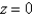 and
and 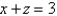
A)
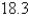
B)
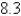
C)
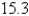
D)
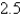
E)
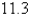
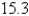
4
Express the triple integral 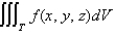 as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes
as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes 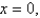
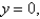
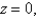 and
and 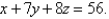
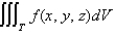 as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes
as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes 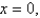
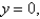
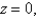 and
and 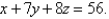

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the triple integral.Round your answer to one decimal place. 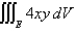
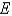 lies under the plane
lies under the plane 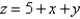 and above the region in the
and above the region in the 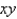 -plane bounded by the curves
-plane bounded by the curves 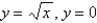 ,and
,and 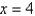
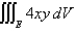
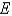 lies under the plane
lies under the plane 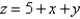 and above the region in the
and above the region in the 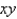 -plane bounded by the curves
-plane bounded by the curves 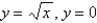 ,and
,and 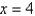

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
6
Find the mass of the solid E,if E is the cube given by 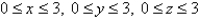 and the density function
and the density function 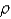 is
is 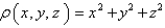
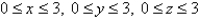 and the density function
and the density function 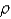 is
is 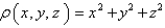

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
7
Express the volume of the wedge in the first octant that is cut from the cylinder 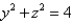 by the planes
by the planes 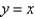 and
and 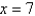 as an iterated integral with respect to z then to y then to x.
as an iterated integral with respect to z then to y then to x.
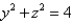 by the planes
by the planes 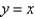 and
and 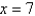 as an iterated integral with respect to z then to y then to x.
as an iterated integral with respect to z then to y then to x.
Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
8
Sketch the solid whose volume is given by the iterated integral 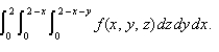
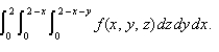

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate the triple integral.Round your answer to one decimal place. 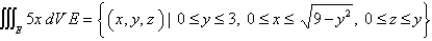
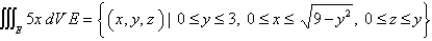

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
10
Express the integral as an iterated integral of the form 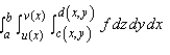 where E is the solid bounded by the surfaces
where E is the solid bounded by the surfaces 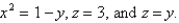
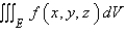
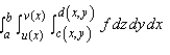 where E is the solid bounded by the surfaces
where E is the solid bounded by the surfaces 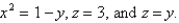
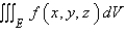

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
11
Calculate the iterated integral. 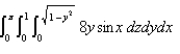
A)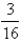
B) 8
C)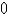
D)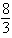
E) None of these
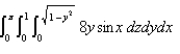
A)
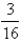
B) 8
C)
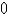
D)
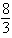
E) None of these

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck


