Exam 12: Extension E: Multiple Integrals
Exam 1: Extension A: Functions and Models20 Questions
Exam 1: Extension B: Functions and Models5 Questions
Exam 1: Extension C: Functions and Models8 Questions
Exam 1: Extension D: Functions and Models12 Questions
Exam 1: Extension E: Functions and Models7 Questions
Exam 1: Extension F: Functions and Models5 Questions
Exam 2: Extension A: Limits and Derivatives9 Questions
Exam 2: Extension B: Limits and Derivatives5 Questions
Exam 2: Extension C: Limits and Derivatives6 Questions
Exam 2: Extension D: Limits and Derivatives6 Questions
Exam 2: Extension E : Limits and Derivatives5 Questions
Exam 2: Extension F: Limits and Derivatives5 Questions
Exam 2: Extension G: Limits and Derivatives10 Questions
Exam 2: Extension H: Limits and Derivatives5 Questions
Exam 3: Extension A: Differentiation Rules5 Questions
Exam 3: Extension B: Differentiation Rules11 Questions
Exam 3: Extension C: Differentiation Rules8 Questions
Exam 3: Extension D: Differentiation Rules5 Questions
Exam 3: Extension E: Differentiation Rules4 Questions
Exam 3: Extension F: Differentiation Rules5 Questions
Exam 3: Extension G: Differentiation Rules5 Questions
Exam 4: Extension A: Applications of Differentiation17 Questions
Exam 4: Extension B: Applications of Differentiation8 Questions
Exam 4: Extension C: Applications of Differentiation15 Questions
Exam 4: Extension D: Applications of Differentiation5 Questions
Exam 4: Extension E: Applications of Differentiation12 Questions
Exam 4: Extension F: Applications of Differentiation5 Questions
Exam 4: Extension G: Applications of Differentiation12 Questions
Exam 5: Extension A: Integrals5 Questions
Exam 5: Extension B: Integrals10 Questions
Exam 5: Extension C: Integrals7 Questions
Exam 5: Extension D: Integrals5 Questions
Exam 5: Extension E: Integrals7 Questions
Exam 6: Extension A: Applications of Integration9 Questions
Exam 6: Extension B: Applications of Integration14 Questions
Exam 6: Extension C: Applications of Integration7 Questions
Exam 6: Extension D: Applications of Integration5 Questions
Exam 6: Extension E: Applications of Integration5 Questions
Exam 6: Extension F: Applications of Integration6 Questions
Exam 7: Extension A: Differential Equations11 Questions
Exam 7: Extension B: Differential Equations13 Questions
Exam 7: Extension C: Differential Equations5 Questions
Exam 7: Extension D: Differential Equations8 Questions
Exam 7: Extension E: Differential Equations7 Questions
Exam 7: Extension F: Differential Equations16 Questions
Exam 7: Extension G: Differential Equations10 Questions
Exam 8: Extension A: Infinte Sequences and Series6 Questions
Exam 8: Extension B: Infinte Sequences and Series11 Questions
Exam 8: Extension C: Infinte Sequences and Series7 Questions
Exam 8: Extension D: Infinte Sequences and Series5 Questions
Exam 8: Extension E: Infinte Sequences and Series6 Questions
Exam 8: Extension F: Infinte Sequences and Series5 Questions
Exam 8: Extension G: Infinte Sequences and Series8 Questions
Exam 8: Extension H: Infinte Sequences and Series5 Questions
Exam 9: Extension A: Vectors and the Geometry of Space5 Questions
Exam 9: Extension B: Vectors and the Geometry of Space5 Questions
Exam 9: Extension C: Vectors and the Geometry of Space5 Questions
Exam 9: Extension D: Vectors and the Geometry of Space6 Questions
Exam 9: Extension E: Vectors and the Geometry of Space9 Questions
Exam 10: Extension A: Vector Functions9 Questions
Exam 10: Extension B: Vector Functions5 Questions
Exam 10: Extension C: Vector Functions5 Questions
Exam 10: Extension D: Vector Functions7 Questions
Exam 10: Extension E: Vector Functions10 Questions
Exam 10: Extension F: Vector Functions4 Questions
Exam 10: Extension H: Vector Functions5 Questions
Exam 10: Extension G: Vector Functions9 Questions
Exam 10: Extension H: Vector Functions14 Questions
Exam 11: Extension A: Partial Derivatives5 Questions
Exam 11: Extension B: Partial Derivatives13 Questions
Exam 11: Extension C: Partial Derivatives17 Questions
Exam 11: Extension D: Partial Derivatives8 Questions
Exam 11: Extension E: Partial Derivatives5 Questions
Exam 11: Extension F: Partial Derivatives5 Questions
Exam 11: Extension G: Partial Derivatives14 Questions
Exam 11: Extension H: Partial Derivatives6 Questions
Exam 12: Extension A: Multiple Integrals5 Questions
Exam 12: Extension B: Multiple Integrals10 Questions
Exam 12: Extension C: Multiple Integrals11 Questions
Exam 12: Extension D: Multiple Integrals5 Questions
Exam 12: Extension E: Multiple Integrals11 Questions
Exam 12: Extension F: Multiple Integrals5 Questions
Exam 12: Extension G: Multiple Integrals6 Questions
Exam 12: Extension H: Multiple Integrals6 Questions
Exam 13: Extension A: Vector Calculus5 Questions
Exam 13: Extension B: Vector Calculus7 Questions
Exam 13: Extension C: Vector Calculus5 Questions
Exam 13: Extension D: Vector Calculus6 Questions
Exam 13: Extension E: Vector Calculus10 Questions
Exam 13: Extension F: Vector Calculus5 Questions
Exam 13: Extension G: Vector Calculus5 Questions
Exam 13: Extension H: Vector Calculus9 Questions
Exam 13: Extension I: Vector Calculus3 Questions
Select questions type
Find the mass of the solid S bounded by the paraboloid 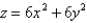 and the plane
and the plane 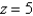 if S has constant density 3.
if S has constant density 3.
Free
(Multiple Choice)
4.8/5  (41)
(41)
Correct Answer:
E
Find the moment of inertia about the y-axis for a cube of constant density 3 and side length 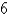 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.
Free
(Essay)
4.7/5  (41)
(41)
Correct Answer:
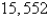
Use a triple integral to find the volume of the solid bounded by 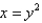 and the planes
and the planes 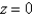 and
and 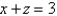
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
C
Find the mass of the solid E,if E is the cube given by 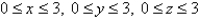 and the density function
and the density function 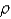 is
is 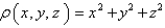
(Essay)
4.8/5  (23)
(23)
Express the integral as an iterated integral of the form 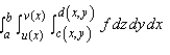 where E is the solid bounded by the surfaces
where E is the solid bounded by the surfaces 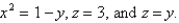
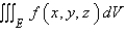
(Essay)
4.8/5  (41)
(41)
Express the volume of the wedge in the first octant that is cut from the cylinder 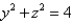 by the planes
by the planes 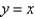 and
and 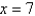 as an iterated integral with respect to z then to y then to x.
as an iterated integral with respect to z then to y then to x.
(Essay)
4.9/5  (37)
(37)
Evaluate the triple integral.Round your answer to one decimal place. 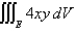
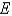 lies under the plane
lies under the plane 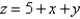 and above the region in the
and above the region in the 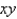 -plane bounded by the curves
-plane bounded by the curves 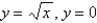 ,and
,and 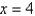
(Essay)
4.7/5  (40)
(40)
Express the triple integral 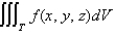 as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes
as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes 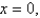
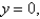
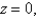 and
and 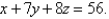
(Essay)
4.7/5  (27)
(27)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)