Deck 1: Introduction and Vectors
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/69
Play
Full screen (f)
Deck 1: Introduction and Vectors
1
One U.S.fluid gallon contains a volume of 231 cubic inches.How many liters of gasoline would you have to buy in Canada to fill a 14-gallon tank? (Note: 1L = 10+3 cm3. )
A)53
B)21
C)14
D)8.0
E)4.0
A)53
B)21
C)14
D)8.0
E)4.0
53
2
John and Linda are arguing about the definition of density.John says the density of an object is proportional to its mass.Linda says the object's mass is proportional to its density and to its volume.Which one,if either,is correct?
A)They are both wrong.
B)John is correct,but Linda is wrong.
C)John is wrong,but Linda is correct.
D)They are both correct.
E)They are free to redefine density as they wish.
A)They are both wrong.
B)John is correct,but Linda is wrong.
C)John is wrong,but Linda is correct.
D)They are both correct.
E)They are free to redefine density as they wish.
They are both correct.
3
Which one of the quantities below has dimensions equal to ?
A)mv
B)mv2
C)
D)mrv
E)
A)mv
B)mv2
C)
D)mrv
E)
4
If you drove day and night without stopping for one year without exceeding the legal highway speed limit in the United States,the maximum number of miles you could drive would be closest to:
A)8 700.
B)300 000.
C)500 000.
D)1 000 000.
E)32 000 000.
A)8 700.
B)300 000.
C)500 000.
D)1 000 000.
E)32 000 000.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
5
If each frame of a motion picture film is 35 cm high,and 24 frames go by in a second,estimate how many frames are needed to show a two hour long movie.
A)1 400
B)25 000
C)50 000
D)170 000
E)This cannot be determined without knowing how many reels were used.
A)1 400
B)25 000
C)50 000
D)170 000
E)This cannot be determined without knowing how many reels were used.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following products of ratios gives the conversion factor to convert miles per hour to meters per second ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
7
One number has three significant figures and another number has four significant figures.If these numbers are added,subtracted,multiplied,or divided,which operation can produce the greatest number of significant figures?
A)the addition
B)the subtraction
C)the multiplication
D)the division
E)All the operations result in the same number of significant figures.
A)the addition
B)the subtraction
C)the multiplication
D)the division
E)All the operations result in the same number of significant figures.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
8
The density of an object is defined as:
A)the volume occupied by each unit of mass.
B)the amount of mass for each unit of volume.
C)the weight of each unit of volume.
D)the amount of the substance that has unit volume and unit mass.
E)the amount of the substance that contains as many particles as 12 grams of the carbon-12 isotope.
A)the volume occupied by each unit of mass.
B)the amount of mass for each unit of volume.
C)the weight of each unit of volume.
D)the amount of the substance that has unit volume and unit mass.
E)the amount of the substance that contains as many particles as 12 grams of the carbon-12 isotope.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
9
The answer to a question is [MLT - 1].The question is "What are the dimensions of
A)mr?"
B)mvr?"
C)ma?"
D)mat?"
E) ?"
A)mr?"
B)mvr?"
C)ma?"
D)mat?"
E) ?"

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
10
The quantity with the same units as force times time,Ft,with dimensions MLT - 1 is
A)mv
B)mvr
C)mv2r
D)ma
E)
A)mv
B)mvr
C)mv2r
D)ma
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
11
A standard exam page is 8.5 inches by 11 inches.An exam that is 2.0 mm thick has a volume of
A)1.9 * 104 mm3.
B)4.7 * 104 mm3.
C)1.2 *105 mm3.
D)3.1 * 105 mm3.
E)3.1 * 103 mm3.
A)1.9 * 104 mm3.
B)4.7 * 104 mm3.
C)1.2 *105 mm3.
D)3.1 * 105 mm3.
E)3.1 * 103 mm3.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
12
The equation for the change of position of a train starting at x = 0 m is given by .The dimensions of b are
A)T - 3
B)LT - 3
C)LT - 2
D)LT - 1
E)L - 1T - 1
A)T - 3
B)LT - 3
C)LT - 2
D)LT - 1
E)L - 1T - 1

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
13
One mole of the carbon-12 isotope contains 6.022 * 1023 atoms.What volume in m3 would be needed to store one mole of cube-shaped children's blocks 2.00 cm long on each side?
A)4.8 * 1018
B)1.2 *1022
C)6.0 * 1023
D)1.2 *1024
E)4.8 *1024
A)4.8 * 1018
B)1.2 *1022
C)6.0 * 1023
D)1.2 *1024
E)4.8 *1024

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following products of ratios gives the conversion factors to convert meters per second to miles per hour ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
15
Find the average density of a red giant star with a mass of 20 * 1030 kg (approximately 10 solar masses)and a radius of 150 *109 m (equal to the Earth's distance from the sun).
A)1.41*10-4 kg/m3
B)0.007 kg/m3
C)1.41 kg/m3
D)710 kg/m3
E)1.41*10 - 3 kg/m3
A)1.41*10-4 kg/m3
B)0.007 kg/m3
C)1.41 kg/m3
D)710 kg/m3
E)1.41*10 - 3 kg/m3

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following quantities has the same dimensions as kinetic energy, ? Note: [a] = [g] = LT - 2;[h] = L and [v] = LT - 1.
A)ma
B)mvx
C)mvt
D)mgh
E)mgt
A)ma
B)mvx
C)mvt
D)mgh
E)mgt

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
17
Which quantity can be converted from the English system to the metric system by the conversion factor ?
A)feet per second
B)feet per hour
C)miles per second
D)miles per hour
E)miles per minute
A)feet per second
B)feet per hour
C)miles per second
D)miles per hour
E)miles per minute

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
18
The term occurs in Bernoulli's equation in Chapter 15,with being the density of a fluid and v its speed.The dimensions of this term are
A)M - 1L5T2
B)MLT2
C)ML - 1T - 2
D)M - 1L9T - 2
E)M - 1L3T - 2
A)M - 1L5T2
B)MLT2
C)ML - 1T - 2
D)M - 1L9T - 2
E)M - 1L3T - 2

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
19
Find the average density of a white dwarf star if it has a mass equal to that of the sun (2.0 * 1030 kg)and a radius equal to that of the Earth (6.4*106 m).
A)9.0 * 106 kg/m3
B)1.8* 107 kg/m3
C)1.8 * 109 kg/m3
D)3.6 * 1010 kg/m3
E)9.0 *107 kg/m3
A)9.0 * 106 kg/m3
B)1.8* 107 kg/m3
C)1.8 * 109 kg/m3
D)3.6 * 1010 kg/m3
E)9.0 *107 kg/m3

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
20
Spike claims that dimensional analysis shows that the correct expression for change in velocity, ,is ,where m is mass,t is time,and F is the magnitude of force.Carla says that can't be true because the dimensions of force are .Which one,if either,is correct?
A)Spike,because .
B)Spike,because .
C)Carla,because .
D)Carla,because .
E)Spike,because the dimensions of force are .
A)Spike,because .
B)Spike,because .
C)Carla,because .
D)Carla,because .
E)Spike,because the dimensions of force are .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
21
Vectors and are shown.What is the magnitude of a vector if ? 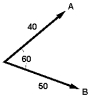
A)46
B)10
C)30
D)78
E)90

A)46
B)10
C)30
D)78
E)90

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
22
Given that and ,what is ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
23
Exhibit 3-3 The vectors , ,and are shown below. 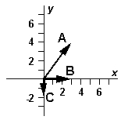 Use this exhibit to answer the following question(s).
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-3.Which diagram below correctly represents ?
A)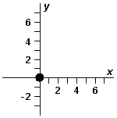
B)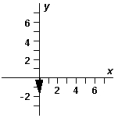
C)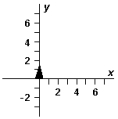
D)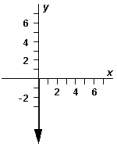
E)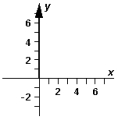
 Use this exhibit to answer the following question(s).
Use this exhibit to answer the following question(s).-Refer to Exhibit 3-3.Which diagram below correctly represents ?
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
24
Given that and ,what is ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
25
If and ,what is the direction of the vector ?
A)-49
B)-41
C)-90
D)+49
E)+21
A)-49
B)-41
C)-90
D)+49
E)+21

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
26
A vector, ,when added to the vector yields a resultant vector which is in the positive y direction and has a magnitude equal to that of .What is the magnitude of ?
A)3.2
B)6.3
C)9.5
D)18
E)5
A)3.2
B)6.3
C)9.5
D)18
E)5

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
27
If vector is added to vector ,the result is .If is subtracted from ,the result is .What is the direction of (to the nearest degree)?
A)225
B)221
C)230
D)236
E)206
A)225
B)221
C)230
D)236
E)206

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
28
A rectangle has a length of 1.323 m and a width of 4.16 m.Using significant figure rules,what is the area of this rectangle?
A)5.503 68 m2
B)5.503 7 m2
C)5.504 m2
D)5.50 m2
E)5.5 m2
A)5.503 68 m2
B)5.503 7 m2
C)5.504 m2
D)5.50 m2
E)5.5 m2

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
29
If and ,what is the magnitude of the vector ?
A)42
B)22
C)64
D)90
E)13
A)42
B)22
C)64
D)90
E)13

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
30
Anthony has added the vectors listed below and gotten the result .What errors has he made?
A)He lost the minus sign in vector .
B)He read the in as .
C)He lost the minus sign in vector .
D)All of the above are correct.
E)Only (a)and (b)above are correct.
A)He lost the minus sign in vector .
B)He read the in as .
C)He lost the minus sign in vector .
D)All of the above are correct.
E)Only (a)and (b)above are correct.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
31
Given two non-zero vectors, and ,such that ,the sum satisfies
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
32
The diagram below shows 3 vectors which sum to zero,all of equal length.Which statement below is true? 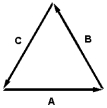
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
33
Given that and ,what is ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
34
If vector is added to vector ,the result is .If is subtracted from ,the result is .What is the magnitude of ?
A)5.1
B)4.1
C)5.4
D)5.8
E)8.2
A)5.1
B)4.1
C)5.4
D)5.8
E)8.2

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
35
Dana says any vector can be represented as the sum of two vectors: .Ardis says any vector can be represented as the difference of two vectors: .Which one,if either,is correct?
A)They are both wrong: every vector is unique.
B)Dana is correct: Any vector can be represented as a sum of components and not as a difference.
C)Ardis is correct: Any vector can be represented as a difference of vector components and not as a sum.
D)They are both correct: A difference of vectors is a sum
.
E)They are both wrong: Vectors can be moved as long as they keep the same magnitude and direction.
A)They are both wrong: every vector is unique.
B)Dana is correct: Any vector can be represented as a sum of components and not as a difference.
C)Ardis is correct: Any vector can be represented as a difference of vector components and not as a sum.
D)They are both correct: A difference of vectors is a sum
.
E)They are both wrong: Vectors can be moved as long as they keep the same magnitude and direction.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
36
Adding vectors and by the graphical method gives the same result for + and +
If both additions are done graphically from the same origin,the resultant is the vector that goes from the tail of the first vector to the tip of the second vector,i.e,it is represented by a diagonal of the parallelogram formed by showing both additions in the same figure.Note that a parallelogram has 2 diagonals.Keara says that the sum of two vectors by the parallelogram method is
Shamu says it is
Both used the parallelogram method,but one used the wrong diagonal.Which one of the vector pairs below contains the original two vectors?
A) ;
B) ;
C) ;
D) ;
E) ;
If both additions are done graphically from the same origin,the resultant is the vector that goes from the tail of the first vector to the tip of the second vector,i.e,it is represented by a diagonal of the parallelogram formed by showing both additions in the same figure.Note that a parallelogram has 2 diagonals.Keara says that the sum of two vectors by the parallelogram method is
Shamu says it is
Both used the parallelogram method,but one used the wrong diagonal.Which one of the vector pairs below contains the original two vectors?
A) ;
B) ;
C) ;
D) ;
E) ;

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 3-3 The vectors , ,and are shown below.  Use this exhibit to answer the following question(s).
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-3.Which diagram below correctly represents ?
A)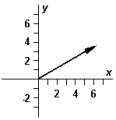
B)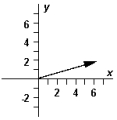
C)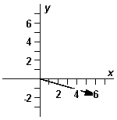
D)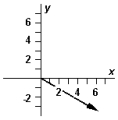
E)
 Use this exhibit to answer the following question(s).
Use this exhibit to answer the following question(s).-Refer to Exhibit 3-3.Which diagram below correctly represents ?
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
38
Given the statement that ,what can we conclude?
A) and .
B)
C) and .
D)Any one of the answers above is correct.
E)Only (a)and (b)may be correct.
A) and .
B)
C) and .
D)Any one of the answers above is correct.
E)Only (a)and (b)may be correct.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
39
A vector is added to .The resultant vector is in the positive x direction and has a magnitude equal to that of .What is the direction of ?
A)74
B)100
C)-81
D)-62
E)106
A)74
B)100
C)-81
D)-62
E)106

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
40
A vector is added to .The resultant vector is in the positive x direction and has a magnitude equal to .What is the magnitude of ?
A)11
B)5.1
C)7.1
D)8.3
E)12.2
A)11
B)5.1
C)7.1
D)8.3
E)12.2

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
41
The vector has components +5 and +7 along the x and y axes respectively.If the vector is now rotated 90 degrees counterclockwise relative to the original axes,the vector's components are now
A)-7;-5.
B)7;-5.
C)-7;5.
D)7;5.
E)7;0.
A)-7;-5.
B)7;-5.
C)-7;5.
D)7;5.
E)7;0.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
42
When three vectors, , ,and are placed head to tail,the vector sum .If the vectors all have the same magnitude,the angle between the directions of any two adjacent vectors is
A)30
B)60
C)90
D)120
E)150
A)30
B)60
C)90
D)120
E)150

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 3-1
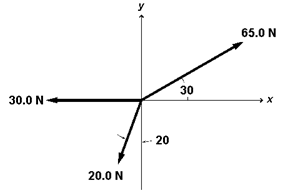
The three forces shown act on a particle. Use this exhibit to answer the following question(s)..
-Refer to Exhibit 3-1.What is the direction of the resultant of these three forces?
A)35
B)45
C)65
D)55
E)85

The three forces shown act on a particle. Use this exhibit to answer the following question(s)..
-Refer to Exhibit 3-1.What is the direction of the resultant of these three forces?
A)35
B)45
C)65
D)55
E)85

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
44
The displacement of the tip of the 10 cm long minute hand of a clock between 12:15 A.M.and 12:45 P.M.is:
A)10 cm,90
B)10 cm,180
C)10 cm,4 500
D)20 cm,180
E)20 cm,540
A)10 cm,90
B)10 cm,180
C)10 cm,4 500
D)20 cm,180
E)20 cm,540

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
45
Starting from one oasis,a camel walks 25 km in a direction 30 south of west and then walks 30 km toward the north to a second oasis.What distance separates the two oases?
A)15 km
B)48 km
C)28 km
D)53 km
E)55 km
A)15 km
B)48 km
C)28 km
D)53 km
E)55 km

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
46
Which statement is true about the unit vectors î, ĵ and k̂ ?
A)Their directions are defined by a left-handed coordinate system.
B)The angle between any two is 90 degrees.
C)Each has a length of 1 m.
D)If î is directed east and ĵ is directed south, k̂ points up out of the surface.
E)All of the above.
A)Their directions are defined by a left-handed coordinate system.
B)The angle between any two is 90 degrees.
C)Each has a length of 1 m.
D)If î is directed east and ĵ is directed south, k̂ points up out of the surface.
E)All of the above.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
47
Starting from one oasis,a camel walks 25 km in a direction 30 south of west and then walks 30 km toward the north to a second oasis.What is the direction from the first oasis to the second oasis?
A)21 N of W
B)39 W of N
C)69 N of W
D)51 W of N
E)42 W of N
A)21 N of W
B)39 W of N
C)69 N of W
D)51 W of N
E)42 W of N

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
48
Exhibit 3-1

The three forces shown act on a particle. Use this exhibit to answer the following question(s)..
Refer to Exhibit 3-1.What is the magnitude of the resultant of these three forces?
A)27.0 N
B)33.2 N
C)36.3 N
D)23.8 N
E)105 N

The three forces shown act on a particle. Use this exhibit to answer the following question(s)..
Refer to Exhibit 3-1.What is the magnitude of the resultant of these three forces?
A)27.0 N
B)33.2 N
C)36.3 N
D)23.8 N
E)105 N

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
49
Exhibit 3-2
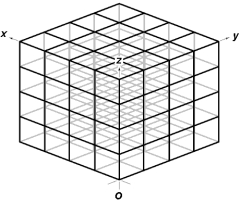
A child starts at one corner of a cubical jungle gym in a playground and climbs up to the diagonally opposite corner.The original corner is the coordinate origin,and the x,y and z axes are oriented along the jungle gym edges.The length of each side is 2 m. Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-2.The child's displacement is:
A)
B)
C)
D)
E)

A child starts at one corner of a cubical jungle gym in a playground and climbs up to the diagonally opposite corner.The original corner is the coordinate origin,and the x,y and z axes are oriented along the jungle gym edges.The length of each side is 2 m. Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-2.The child's displacement is:
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
50
If vector is added to vector ,the result is a third vector that is perpendicular to and has a magnitude equal to 3 .What is the ratio of the magnitude of to that of ?
A)1.8
B)2.2
C)3.2
D)1.3
E)1.6
A)1.8
B)2.2
C)3.2
D)1.3
E)1.6

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 3-4
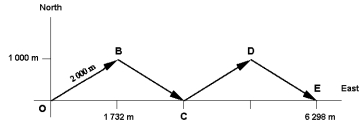
The diagram below shows the path taken by a sailboat tacking sideways because it cannot sail directly into the wind. Use this exhibit to answer the following question(s).
Refer to Exhibit 3-4.The total distance it travels is
A)1 000 m.
B)1 732 m.
C)2 000 m.
D)6 298 m.
E)8 000 m.

The diagram below shows the path taken by a sailboat tacking sideways because it cannot sail directly into the wind. Use this exhibit to answer the following question(s).
Refer to Exhibit 3-4.The total distance it travels is
A)1 000 m.
B)1 732 m.
C)2 000 m.
D)6 298 m.
E)8 000 m.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
52
If two collinear vectors and are added,the resultant has a magnitude equal to 4.0.If is subtracted from ,the resultant has a magnitude equal to 8.0.What is the magnitude of ?
A)2.0
B)3.0
C)4.0
D)5.0
E)6.0
A)2.0
B)3.0
C)4.0
D)5.0
E)6.0

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
53
Exhibit 3-2

A child starts at one corner of a cubical jungle gym in a playground and climbs up to the diagonally opposite corner.The original corner is the coordinate origin,and the x,y and z axes are oriented along the jungle gym edges.The length of each side is 2 m. Use this exhibit to answer the following question(s).
Refer to Exhibit 3-2.What is the child's distance from her starting position?
A)2.8 m
B)3.5 m
C)6.0 m
D)6.9 m
E)12.0 m

A child starts at one corner of a cubical jungle gym in a playground and climbs up to the diagonally opposite corner.The original corner is the coordinate origin,and the x,y and z axes are oriented along the jungle gym edges.The length of each side is 2 m. Use this exhibit to answer the following question(s).
Refer to Exhibit 3-2.What is the child's distance from her starting position?
A)2.8 m
B)3.5 m
C)6.0 m
D)6.9 m
E)12.0 m

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
54
A student decides to spend spring break by driving 50 miles due east,then 50 miles 30 degrees south of east,then 50 miles 30 degrees south of that direction,and to continue to drive 50 miles deviating by 30 degrees each time until he returns to his original position.How far will he drive,and how many vectors must he sum to calculate his displacement?
A)0,0
B)0,8
C)0,12
D)400 mi,8
E)600 mi,12
A)0,0
B)0,8
C)0,12
D)400 mi,8
E)600 mi,12

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
55
Exhibit 3-4

The diagram below shows the path taken by a sailboat tacking sideways because it cannot sail directly into the wind. Use this exhibit to answer the following question(s).
Refer to Exhibit 3-4.The total displacement of the sailboat,the vector sum of its displacements OB,BC,CD and DE,is
A)1 732 m,East.
B)2 000 m,Northeast.
C)6 298 m,East.
D)8 000 m,Southeast.
E)8 000 m,East.

The diagram below shows the path taken by a sailboat tacking sideways because it cannot sail directly into the wind. Use this exhibit to answer the following question(s).
Refer to Exhibit 3-4.The total displacement of the sailboat,the vector sum of its displacements OB,BC,CD and DE,is
A)1 732 m,East.
B)2 000 m,Northeast.
C)6 298 m,East.
D)8 000 m,Southeast.
E)8 000 m,East.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
56
Vectors and have equal magnitudes.Which statement is always true?
A) .
B) .
C) is perpendicular to .
D) is perpendicular to .
E)The magnitude of equals the magnitude of .
A) .
B) .
C) is perpendicular to .
D) is perpendicular to .
E)The magnitude of equals the magnitude of .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
57
When vector is added to vector ,which has a magnitude of 5.0,the vector representing their sum is perpendicular to and has a magnitude that is twice that of .What is the magnitude of ?
A)2.2
B)2.5
C)4.5
D)5.0
E)7.0
A)2.2
B)2.5
C)4.5
D)5.0
E)7.0

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
58
The rectangular coordinates of a point are (5.00,y)and the polar coordinates of this point are (r,67.4°).What is the value of the polar coordinate r in this case?
A)1.92
B)4.62
C)12.0
D)13.0
E)More information is needed.
A)1.92
B)4.62
C)12.0
D)13.0
E)More information is needed.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
59
The vector has components +5 and +7 along the x and y axes respectively.Along a set of axes rotated 90 degrees counterclockwise relative to the original axes,the vector's components are
A)-7;-5.
B)7;-5.
C)-7;5.
D)7;5.
E)7;0.
A)-7;-5.
B)7;-5.
C)-7;5.
D)7;5.
E)7;0.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
60
If two collinear vectors and are added,the resultant has a magnitude equal to 4.0.If is subtracted from ,the resultant has a magnitude equal to 8.0.What is the magnitude of ?
A)2.0
B)3.0
C)4.0
D)5.0
E)6.0
A)2.0
B)3.0
C)4.0
D)5.0
E)6.0

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
61
What is the mass of air in a room that measures 5.0 m * 8.0 m * 3.0 m? (The density of air is 1/800 that of water).

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
62
A vector starts at coordinate (3.0,4.0)and ends at coordinate (-2.0,16.0).What are the magnitude and direction of this vector?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
63
The basic function of a carburetor of an automobile is to atomize the gasoline and mix it with air to promote rapid combustion.As an example,assume that 30 cm3 of gasoline is atomized into N spherical droplets,each with a radius of 2.0 *10 - 5 m.What is the total surface area of these N spherical droplets?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
64
The standard kilogram is a platinum-iridium cylinder 39 mm in height and 39 mm in diameter.What is the density of the material?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
65
A 2.00 m by 3.00 m plate of aluminum has a mass of 324 kg.What is the thickness of the plate? (The density of aluminum is 2.70 * 103 kg/m3. )

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
66
What two vectors are each the same magnitude as and perpendicular to 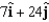 ?
?
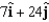 ?
?
Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
67
A problem may be solved more easily when alternative representations are used.The best strategy is to formulate representations in an order that assists in understanding the physical principles involved.Of the orders given below,the one that will work best most often is
A)pictorial representation,mathematical representation,tabular representation,mental representation.
B)pictorial representation,mental representation,mathematical representation,tabular representation.
C)mathematical representation,pictorial representation,tabular representation,mental representation.
D)mathematical representation,tabular representation,mental representation,pictorial representation.
E)mental representation,pictorial representation,tabular representation,mathematical representation.
A)pictorial representation,mathematical representation,tabular representation,mental representation.
B)pictorial representation,mental representation,mathematical representation,tabular representation.
C)mathematical representation,pictorial representation,tabular representation,mental representation.
D)mathematical representation,tabular representation,mental representation,pictorial representation.
E)mental representation,pictorial representation,tabular representation,mathematical representation.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
68
In what quadrant are both the sine and tangent negative?
A)1st
B)2nd
C)3rd
D)4th
E)This cannot happen.
A)1st
B)2nd
C)3rd
D)4th
E)This cannot happen.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
69
Two vectors starting at the same origin have equal and opposite x components.Is it possible for the two vectors to be perpendicular to each other? Justify your answer.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck


