Exam 1: Introduction and Vectors
Exam 1: Introduction and Vectors69 Questions
Exam 2: Motion in One Dimension55 Questions
Exam 3: Motion in Two Dimensions82 Questions
Exam 4: The Laws of Motion97 Questions
Exam 5: More Applications of Newtons Laws80 Questions
Exam 6: Energy of a System81 Questions
Exam 7: Conservation of Energy77 Questions
Exam 8: Momentum and Collisions84 Questions
Exam 9: Relativity31 Questions
Exam 10: Rotational Motion121 Questions
Exam 11: Gravity,planetary Orbits,and the Hydrogen Atom62 Questions
Exam 12: Oscillatory Motion44 Questions
Exam 13: Mechanical Waves56 Questions
Exam 14: Superposition and Standing Waves57 Questions
Exam 15: Fluid Mechanics48 Questions
Exam 16: Temperature and the Kinetic Theory of Gases54 Questions
Exam 17: Energy in Thermal Processes: the First Law of Thermodynamics69 Questions
Exam 18: Heat Engines,entropy,and the Second Law of Thermodynamics51 Questions
Exam 19: Electric Forces and Electric Fields156 Questions
Exam 20: Electric Potential and Capacitance158 Questions
Exam 21: Current and Direct Current Circuits113 Questions
Exam 22: Magnetic Forces and Magnetic Fields157 Questions
Exam 23: Faradays Law and Inductance76 Questions
Exam 24: Electromagnetic Waves41 Questions
Exam 25: Reflection and Refraction of Light34 Questions
Exam 26: Image Formation by Mirrors and Lenses41 Questions
Exam 27: Wave Optics72 Questions
Exam 28: Quantum Physics69 Questions
Exam 29: Atomic Physics35 Questions
Exam 30: Nuclear Physics62 Questions
Exam 31: Particle Physics31 Questions
Select questions type
What two vectors are each the same magnitude as and perpendicular to ?
Free
(Short Answer)
4.7/5  (40)
(40)
Correct Answer:
and .
A rectangle has a length of 1.323 m and a width of 4.16 m.Using significant figure rules,what is the area of this rectangle?
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
D
If two collinear vectors and are added,the resultant has a magnitude equal to 4.0.If is subtracted from ,the resultant has a magnitude equal to 8.0.What is the magnitude of ?
Free
(Multiple Choice)
4.8/5  (26)
(26)
Correct Answer:
A
Find the average density of a red giant star with a mass of 20 * 1030 kg (approximately 10 solar masses)and a radius of 150 *109 m (equal to the Earth's distance from the sun).
(Multiple Choice)
4.9/5  (39)
(39)
The quantity with the same units as force times time,Ft,with dimensions MLT - 1 is
(Multiple Choice)
4.8/5  (34)
(34)
Vectors and are shown.What is the magnitude of a vector if ? 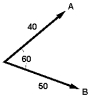
(Multiple Choice)
4.8/5  (38)
(38)
Which quantity can be converted from the English system to the metric system by the conversion factor ?
(Multiple Choice)
4.9/5  (46)
(46)
Dana says any vector can be represented as the sum of two vectors: .Ardis says any vector can be represented as the difference of two vectors: .Which one,if either,is correct?
(Multiple Choice)
4.9/5  (31)
(31)
Which of the following quantities has the same dimensions as kinetic energy, ? Note: [a] = [g] = LT - 2;[h] = L and [v] = LT - 1.
(Multiple Choice)
4.9/5  (33)
(33)
Two vectors starting at the same origin have equal and opposite x components.Is it possible for the two vectors to be perpendicular to each other? Justify your answer.
(Essay)
4.8/5  (45)
(45)
John and Linda are arguing about the definition of density.John says the density of an object is proportional to its mass.Linda says the object's mass is proportional to its density and to its volume.Which one,if either,is correct?
(Multiple Choice)
4.9/5  (35)
(35)
Exhibit 3-3 The vectors , ,and are shown below. 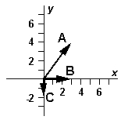 Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-3.Which diagram below correctly represents ?
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-3.Which diagram below correctly represents ?
(Multiple Choice)
4.8/5  (35)
(35)
The displacement of the tip of the 10 cm long minute hand of a clock between 12:15 A.M.and 12:45 P.M.is:
(Multiple Choice)
4.8/5  (36)
(36)
The term occurs in Bernoulli's equation in Chapter 15,with being the density of a fluid and v its speed.The dimensions of this term are
(Multiple Choice)
4.9/5  (36)
(36)
Adding vectors and by the graphical method gives the same result for + and +
If both additions are done graphically from the same origin,the resultant is the vector that goes from the tail of the first vector to the tip of the second vector,i.e,it is represented by a diagonal of the parallelogram formed by showing both additions in the same figure.Note that a parallelogram has 2 diagonals.Keara says that the sum of two vectors by the parallelogram method is
Shamu says it is
Both used the parallelogram method,but one used the wrong diagonal.Which one of the vector pairs below contains the original two vectors?
(Multiple Choice)
4.9/5  (37)
(37)
Which one of the quantities below has dimensions equal to ?
(Multiple Choice)
4.8/5  (33)
(33)
When vector is added to vector ,which has a magnitude of 5.0,the vector representing their sum is perpendicular to and has a magnitude that is twice that of .What is the magnitude of ?
(Multiple Choice)
4.9/5  (37)
(37)
A vector is added to .The resultant vector is in the positive x direction and has a magnitude equal to that of .What is the direction of ?
(Multiple Choice)
4.9/5  (38)
(38)
Anthony has added the vectors listed below and gotten the result .What errors has he made?
(Multiple Choice)
4.9/5  (40)
(40)
If two collinear vectors and are added,the resultant has a magnitude equal to 4.0.If is subtracted from ,the resultant has a magnitude equal to 8.0.What is the magnitude of ?
(Multiple Choice)
4.8/5  (29)
(29)
Showing 1 - 20 of 69
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)