Deck 18: Simplex-Based Sensitivity Analysis and Duality
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/32
Play
Full screen (f)
Deck 18: Simplex-Based Sensitivity Analysis and Duality
1
The improvement in the value of the optimal solution per unit increase in a constraint's right-hand side is
A)the slack value.
B)the dual price.
C)never negative.
D)the 100% rule.
A)the slack value.
B)the dual price.
C)never negative.
D)the 100% rule.
B
2
We can often avoid the process of formulating and solving a modified linear programming problem by using the range of optimality to determine whether a change in an objective function coefficient is large enough to cause a change in the optimal solution.
True
3
Dual prices and ranges for objective function coefficients and right-hand-side values are found by considering
A)dual analysis.
B)optimality analysis.
C)ranging analysis.
D)sensitivity analysis.
A)dual analysis.
B)optimality analysis.
C)ranging analysis.
D)sensitivity analysis.
D
4
The range of optimality is calculated by considering changes in the cj − zj value of the variable in question.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
5
As long as the actual value of the objective function coefficient is within the range of optimality,the current basic feasible solution will remain optimal.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
6
A one-sided range of optimality
A)always occurs for nonbasic variables.
B)always occurs for basic variables.
C)indicates changes in more than one coefficient.
D)indicates changes in a slack variable's coefficient.
A)always occurs for nonbasic variables.
B)always occurs for basic variables.
C)indicates changes in more than one coefficient.
D)indicates changes in a slack variable's coefficient.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
7
The dual price is the improvement in value of the optimal solution per unit increase in a constraint's right-hand-side value.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
8
If the simplex tableau is from a maximization converted from a minimization,the signs and directions of the inequalities that give the objective function ranges will need to be adjusted to apply to the original coefficients.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
9
The range of optimality for a basic variable defines the objective function coefficient values for which that variable will remain part of the current optimal basic feasible solution.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
10
The ranges for which the right-hand-side values are valid are the same as the ranges over which the dual prices are valid.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
11
The range of feasibility indicates right-hand-side values for which
A)the value of the objective function will not change.
B)the values of the decision variables will not change.
C)those variables that are in the basis will not change.
D)more simplex iterations must be performed.
A)the value of the objective function will not change.
B)the values of the decision variables will not change.
C)those variables that are in the basis will not change.
D)more simplex iterations must be performed.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
12
The entries in the associated slack column of the final tableau can also be interpreted as the changes in the values of the current basic variables corresponding to a one-unit increase in the right-hand side.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
13
The dual variable represents the
A)marginal value of the constraint.
B)right-hand-side value of the constraint.
C)artificial variable.
D)technical coefficient of the constraint.
A)marginal value of the constraint.
B)right-hand-side value of the constraint.
C)artificial variable.
D)technical coefficient of the constraint.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
14
The range of optimality is useful only for basic variables.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
15
As long as the objective function coefficient remains within the range of optimality,the variable values will not change although the value of the objective function could.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
16
For the basic feasible solution to remain optimal,
A)all cj − zj values must remain ≤ 0.
B)no objective function coefficients are allowed to change.
C)the value of the objective function must not change.
D)All of these are correct.
A)all cj − zj values must remain ≤ 0.
B)no objective function coefficients are allowed to change.
C)the value of the objective function must not change.
D)All of these are correct.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
17
The dual price for an equality constraint is the zj value for its artificial variable.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
18
A linear programming problem with the objective function 3x1 + 8x2 has the optimal solution x1 = 5,x2 = 6.If c2 decreases by 2 and the range of optimality shows 5 ≤ c2 ≤ 12,the value of Z
A)will decrease by 12.
B)will decrease by 2.
C)will not change.
D)cannot be determined from this information.
A)will decrease by 12.
B)will decrease by 2.
C)will not change.
D)cannot be determined from this information.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
19
Within the concept of duality is the original formulation of a linear programming problem known as the primal problem.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
20
A dual price is associated with each decision variable.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
21
For the following linear programming problem 
the final tableau is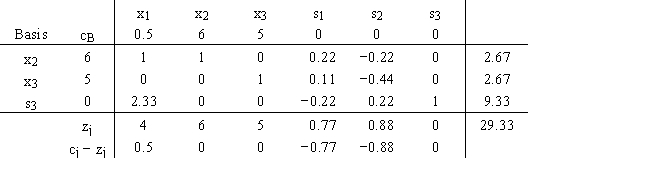
a.Find the range of optimality for c1, c2, c3, c4, c5, and c6.
b.Find the range of feasibility for b1,b2,and b3.

the final tableau is

a.Find the range of optimality for c1, c2, c3, c4, c5, and c6.
b.Find the range of feasibility for b1,b2,and b3.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
22
If the dual price for b1 is 2.7,the range of feasibility is 20 ≤ b1 ≤ 50,and the original value of b1 was 30,which of the following is true?
A)There currently is no slack in the first constraint.
B)We would be willing to pay up to $2.70 per unit for up to 20 more units of resource 1.
C)If only 25 units of resource 1 were available,profit would drop by $13.50.
D)All of these are correct.
A)There currently is no slack in the first constraint.
B)We would be willing to pay up to $2.70 per unit for up to 20 more units of resource 1.
C)If only 25 units of resource 1 were available,profit would drop by $13.50.
D)All of these are correct.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
23
The primal problem is as follows: 
The final tableau for its dual problem is as follows: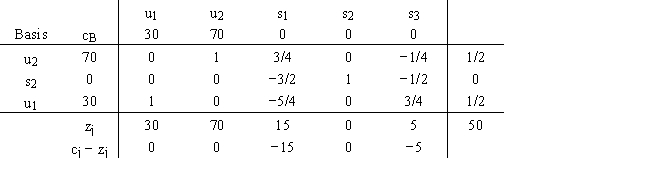
Give the complete solution to the primal problem.

The final tableau for its dual problem is as follows:

Give the complete solution to the primal problem.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
24
Creative Kitchen Tools manufactures a wide line of gourmet cooking tools from stainless steel.For the coming production period,there is demand of 1200 for eight-quart stock pots and unlimited demand for three-quart mixing bowls and large slotted spoons.In the following model,the three variables measure the number of pots,bowls,and spoons to make.The objective function measures profit.Constraint 1 measures steel,constraint 2 measures manufacturing time,constraint 3 measures finishing time,and constraint 4 measures the stock pot demand. 
The final tableau is as follows: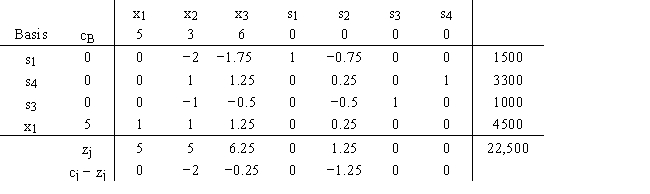
a.Calculate the range of optimality for c1,c2,and c3.
b.Calculate the range of feasibility for b1,b2,b3,and b4.
c.
Suppose that the inventory records were incorrect and the company really has only 14,000 units of steel.What effect will this have on your solution?
d.
Suppose that a cost increase will change the profit on the pots to $4.62.What effect will this have on your solution?
e.
Assume that the cost of time in production and finishing is relevant.Would you be willing to pay a $1.00 premium over the normal cost for 1000 more hours in the production department? What would this do to your solution?

The final tableau is as follows:

a.Calculate the range of optimality for c1,c2,and c3.
b.Calculate the range of feasibility for b1,b2,b3,and b4.
c.
Suppose that the inventory records were incorrect and the company really has only 14,000 units of steel.What effect will this have on your solution?
d.
Suppose that a cost increase will change the profit on the pots to $4.62.What effect will this have on your solution?
e.
Assume that the cost of time in production and finishing is relevant.Would you be willing to pay a $1.00 premium over the normal cost for 1000 more hours in the production department? What would this do to your solution?

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
25
For the following linear programming problem 
the final tableau is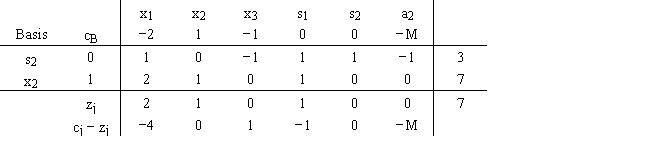
a.Find the range of optimality for c1,c2,c3,c4,c5,and c6.
b.Find the range of feasibility for b1 and b2.

the final tableau is

a.Find the range of optimality for c1,c2,c3,c4,c5,and c6.
b.Find the range of feasibility for b1 and b2.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
26
For the following linear programming problem 
the final tableau is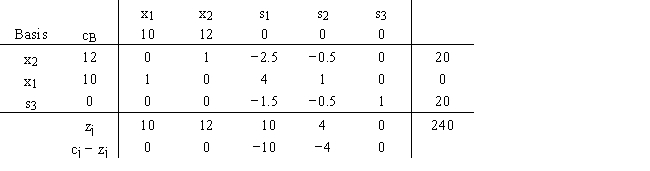
a.Find the range of optimality for c1 and c2.
b.Find the range of feasibility for b1,b2,and b3.
c.Find the dual prices.

the final tableau is

a.Find the range of optimality for c1 and c2.
b.Find the range of feasibility for b1,b2,and b3.
c.Find the dual prices.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
27
Write the dual of the following problem: 


Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
28
For this optimal simplex tableau,the original right-hand sides were 100 and 90.The problem was a maximization. 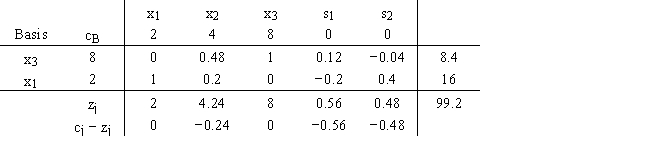
a.What would the new solution be if there had been 150 units available in the first constraint?
b.What would the new solution be if there had been 70 units available in the second constraint?

a.What would the new solution be if there had been 150 units available in the first constraint?
b.What would the new solution be if there had been 70 units available in the second constraint?

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
29
An LP maximization problem with all less-than-or-equal-to constraints and nonnegativity requirements for the decision variables is known as
A)a canonical form for a minimization problem.
B)a canonical form for a maximization problem.
C)always unbounded.
D)None of these are correct.
A)a canonical form for a minimization problem.
B)a canonical form for a maximization problem.
C)always unbounded.
D)None of these are correct.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
30
For this optimal simplex tableau,the right-hand sides for the two original ≥ constraints were 300 and 250.The problem was a minimization. 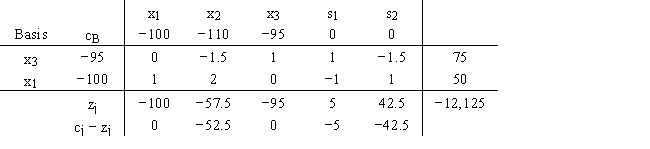
a.What would the new solution be if the right-hand-side value in the first constraint had been 325?
b.What would the new solution be if the right-hand-side value for the second constraint had been 220?
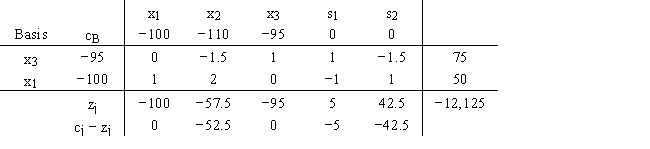
a.What would the new solution be if the right-hand-side value in the first constraint had been 325?
b.What would the new solution be if the right-hand-side value for the second constraint had been 220?

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
31
Write the dual to the following problem. 


Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
32
Given the simplex tableau for the optimal primal solution,
A)the values of the dual variables can be found from the cj − zj values of the slack/surplus variable columns.
B)the values of the dual surplus variables can be found from the cj − zj values of the primal decision variable columns.
C)the value of the dual objective function will be the same as the objective function value for the primal problem.
D)All of these are correct.
A)the values of the dual variables can be found from the cj − zj values of the slack/surplus variable columns.
B)the values of the dual surplus variables can be found from the cj − zj values of the primal decision variable columns.
C)the value of the dual objective function will be the same as the objective function value for the primal problem.
D)All of these are correct.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck


