Exam 18: Simplex-Based Sensitivity Analysis and Duality
Exam 1: Introduction53 Questions
Exam 2: An Introduction to Linear Programming56 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution44 Questions
Exam 4: Linear Programming Applications in Marketing, finance, and OM52 Questions
Exam 5: Advanced Linear Programming Applications39 Questions
Exam 6: Distribution and Network Models62 Questions
Exam 7: Integer Linear Programming52 Questions
Exam 8: Nonlinear Optimization Models45 Questions
Exam 9: Project Scheduling: Pertcpm60 Questions
Exam 10: Inventory Models60 Questions
Exam 11: Waiting Line Models56 Questions
Exam 12: Simulation53 Questions
Exam 13: Decision Analysis80 Questions
Exam 14: Multicriteria Decisions42 Questions
Exam 15: Time Series Analysis and Forecasting53 Questions
Exam 16: Markov Processes36 Questions
Exam 17: Linear Programming: Simplex Method45 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality32 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems39 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming41 Questions
Select questions type
If the simplex tableau is from a maximization converted from a minimization,the signs and directions of the inequalities that give the objective function ranges will need to be adjusted to apply to the original coefficients.
Free
(True/False)
4.9/5  (31)
(31)
Correct Answer:
True
For this optimal simplex tableau,the original right-hand sides were 100 and 90.The problem was a maximization. 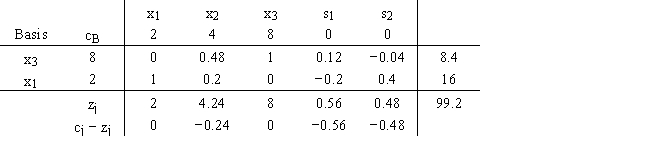
a.What would the new solution be if there had been 150 units available in the first constraint?
b.What would the new solution be if there had been 70 units available in the second constraint?
a.What would the new solution be if there had been 150 units available in the first constraint?
b.What would the new solution be if there had been 70 units available in the second constraint?
Free
(Essay)
4.7/5  (27)
(27)
Correct Answer:

The primal problem is as follows: 
The final tableau for its dual problem is as follows:
The final tableau for its dual problem is as follows: 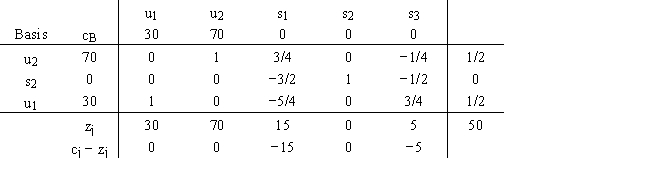
Give the complete solution to the primal problem.
Give the complete solution to the primal problem.
Free
(Essay)
4.9/5  (41)
(41)
Correct Answer:
The complete primal solution is x1 = 15,x2 = 0,x3 = 5,s1 = 0,s2 = 0,Z = 50.
For the following linear programming problem 
the final tableau is
the final tableau is 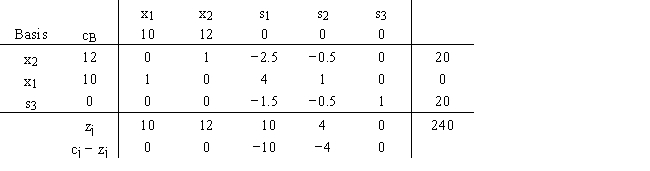
a.Find the range of optimality for c1 and c2.
b.Find the range of feasibility for b1,b2,and b3.
c.Find the dual prices.
a.Find the range of optimality for c1 and c2.
b.Find the range of feasibility for b1,b2,and b3.
c.Find the dual prices.
(Essay)
4.9/5  (28)
(28)
As long as the actual value of the objective function coefficient is within the range of optimality,the current basic feasible solution will remain optimal.
(True/False)
4.8/5  (36)
(36)
For the following linear programming problem 
the final tableau is
the final tableau is 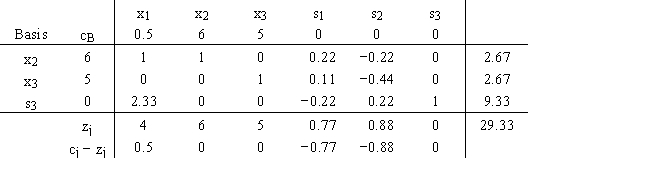
a.Find the range of optimality for c1, c2, c3, c4, c5, and c6.
b.Find the range of feasibility for b1,b2,and b3.
a.Find the range of optimality for c1, c2, c3, c4, c5, and c6.
b.Find the range of feasibility for b1,b2,and b3.
(Essay)
4.7/5  (40)
(40)
An LP maximization problem with all less-than-or-equal-to constraints and nonnegativity requirements for the decision variables is known as
(Multiple Choice)
4.9/5  (24)
(24)
The range of optimality is calculated by considering changes in the cj − zj value of the variable in question.
(True/False)
4.7/5  (38)
(38)
The dual price for an equality constraint is the zj value for its artificial variable.
(True/False)
4.9/5  (39)
(39)
For this optimal simplex tableau,the right-hand sides for the two original ≥ constraints were 300 and 250.The problem was a minimization. 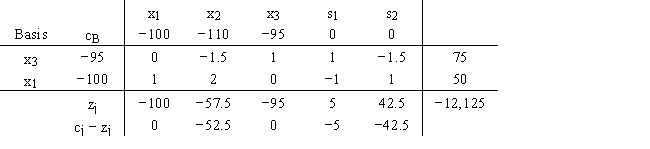
a.What would the new solution be if the right-hand-side value in the first constraint had been 325?
b.What would the new solution be if the right-hand-side value for the second constraint had been 220?
a.What would the new solution be if the right-hand-side value in the first constraint had been 325?
b.What would the new solution be if the right-hand-side value for the second constraint had been 220?
(Essay)
4.7/5  (40)
(40)
The entries in the associated slack column of the final tableau can also be interpreted as the changes in the values of the current basic variables corresponding to a one-unit increase in the right-hand side.
(True/False)
4.8/5  (35)
(35)
Dual prices and ranges for objective function coefficients and right-hand-side values are found by considering
(Multiple Choice)
4.8/5  (25)
(25)
If the dual price for b1 is 2.7,the range of feasibility is 20 ≤ b1 ≤ 50,and the original value of b1 was 30,which of the following is true?
(Multiple Choice)
4.9/5  (28)
(28)
The improvement in the value of the optimal solution per unit increase in a constraint's right-hand side is
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 32
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)