Deck 6: Section 5: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/17
Play
Full screen (f)
Deck 6: Section 5: Differential Equations
1
Find the particular solution of the differential equation 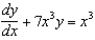 passing through the point
passing through the point 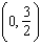 .
.
A)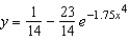
B)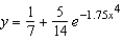
C)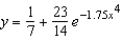
D)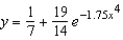
E)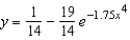
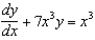 passing through the point
passing through the point 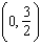 .
.A)
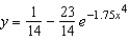
B)
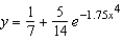
C)
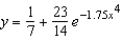
D)
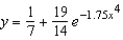
E)
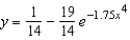
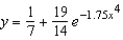
2
Suppose an eight-pound object is dropped from a height of 5000 feet, where the air resistance is proportional to the velocity. Write the velocity as a function of time if its velocity after 7 seconds is approximately -75 feet per second. Use a graphing utility or a computer algebra system. Round numerical answers in your answer to four places.
A)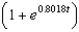
B)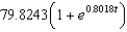
C) 0.8018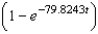
D)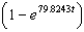
E)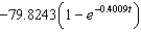
A)
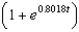
B)
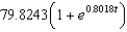
C) 0.8018
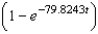
D)
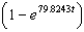
E)
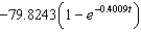
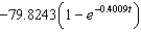
3
A 200-gallon tank is half full of distilled water. At time 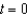 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 5 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 3 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 5 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 3 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
A) 11.61 lbs
B) 64.64 lbs
C) 71.34 lbs
D) 49.39 lbs
E) 82.32 lbs
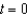 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 5 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 3 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 5 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 3 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.A) 11.61 lbs
B) 64.64 lbs
C) 71.34 lbs
D) 49.39 lbs
E) 82.32 lbs
82.32 lbs
4
A 300-gallon tank is half full of distilled water. At time 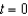 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 8 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 6 gallons per minute. At what time will the tank be full?
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 8 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 6 gallons per minute. At what time will the tank be full?
A) 150 minutes
B) 76 minutes
C) 75 minutes
D) 301 minutes
E) 600 minutes
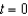 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 8 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 6 gallons per minute. At what time will the tank be full?
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 8 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 6 gallons per minute. At what time will the tank be full?A) 150 minutes
B) 76 minutes
C) 75 minutes
D) 301 minutes
E) 600 minutes

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
5
Find the particular solution of the differential equation 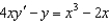 that satisfies the boundary condition
that satisfies the boundary condition 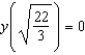 .
.
A)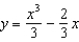
B)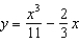
C)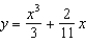
D)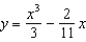
E)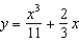
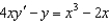 that satisfies the boundary condition
that satisfies the boundary condition 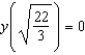 .
.A)
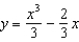
B)
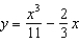
C)
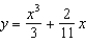
D)
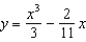
E)
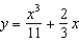

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the Bernoulli differential equation 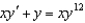 .
.
A)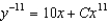
B)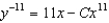
C)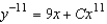
D)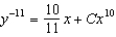
E)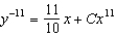
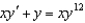 .
.A)
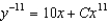
B)
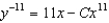
C)
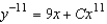
D)
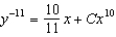
E)
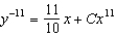

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
7
A 200-gallon tank is full of a solution containing 25 pounds of concentrate. Starting at time 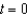 , distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.
, distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.
A) 18.3 min
B) 3.6 min
C) 20.4 min
D) 10.2 min
E) 5.1 min
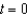 , distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.
, distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the time at which the amount of concentrate in the tank reaches 15 pounds. Round your answer to one decimal place.A) 18.3 min
B) 3.6 min
C) 20.4 min
D) 10.2 min
E) 5.1 min

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the first order linear differential equation. 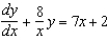
A)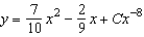
B)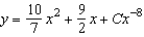
C)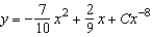
D)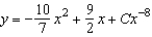
E)
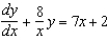
A)
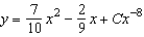
B)
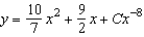
C)
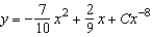
D)
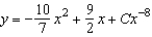
E)


Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the first-order linear differential equation 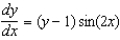 .
.
A)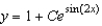
B)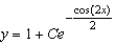
C)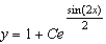
D)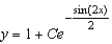
E)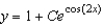
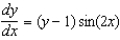 .
.A)
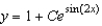
B)
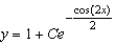
C)
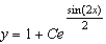
D)
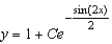
E)
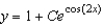

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
10
Use 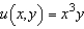 as a integrating factor to find the general solution of the differential equation
as a integrating factor to find the general solution of the differential equation 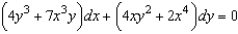 .
.
A)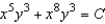
B)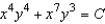
C)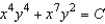
D)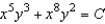
E)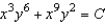
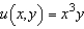 as a integrating factor to find the general solution of the differential equation
as a integrating factor to find the general solution of the differential equation 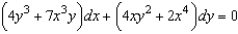 .
.A)
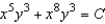
B)
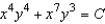
C)
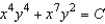
D)
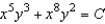
E)
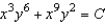

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
11
Find the particular solution of the differential equation 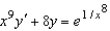 that satisfies the initial condition
that satisfies the initial condition 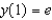 .
.
A)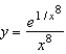
B)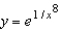
C)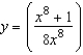
D)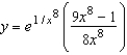
E)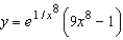
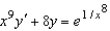 that satisfies the initial condition
that satisfies the initial condition 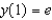 .
.A)
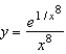
B)
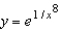
C)
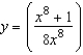
D)
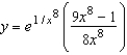
E)
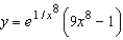

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
12
Assume an object weighing 7 pounds is dropped from a height of 9,000 feet, where the air resistance is proportional to the velocity. Round numerical answers in your answer to two places. (i) Write the velocity as a function of time if the object's velocity after 6 seconds is 3.50 feet per second.
(ii) What is the limiting value of the velocity function?
A) (i)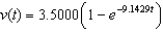 ; (ii) 0
; (ii) 0
B) (i)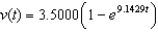 ; (ii) 0
; (ii) 0
C) (i)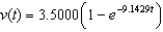 ; (ii) 3.5000
; (ii) 3.5000
D) (i)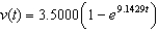 ; (ii) 3.5000
; (ii) 3.5000
E) (i)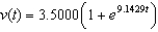 ; (ii) limit does not exist
; (ii) limit does not exist
(ii) What is the limiting value of the velocity function?
A) (i)
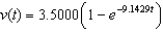 ; (ii) 0
; (ii) 0B) (i)
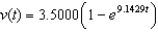 ; (ii) 0
; (ii) 0C) (i)
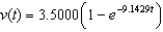 ; (ii) 3.5000
; (ii) 3.5000D) (i)
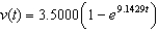 ; (ii) 3.5000
; (ii) 3.5000E) (i)
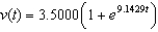 ; (ii) limit does not exist
; (ii) limit does not exist
Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
13
Find the particular solution of the differential equation 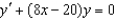 that satisfies the boundary condition
that satisfies the boundary condition 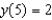 .
.
A)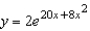
B)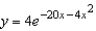
C)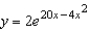
D)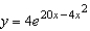
E)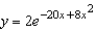
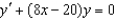 that satisfies the boundary condition
that satisfies the boundary condition 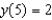 .
.A)
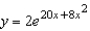
B)
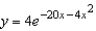
C)
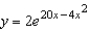
D)
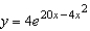
E)
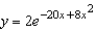

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
14
Find the particular solution of the differential equation 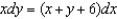 that satisfies the boundary condition
that satisfies the boundary condition 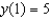 .
.
A)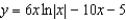
B)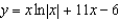
C)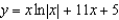
D)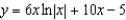
E)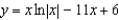
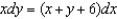 that satisfies the boundary condition
that satisfies the boundary condition 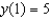 .
.A)
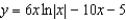
B)
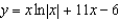
C)
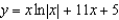
D)
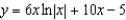
E)
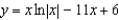

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the first order linear differential equation. 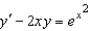
A)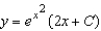
B)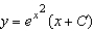
C)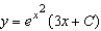
D)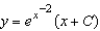
E)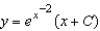
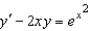
A)
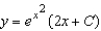
B)
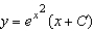
C)
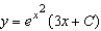
D)
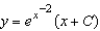
E)
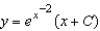

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
16
A 100-gallon tank is full of a solution containing 25 pounds of concentrate. Starting at time 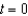 , distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as
, distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as 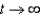 .
.
A) 10
B) 26
C) 25
D) 0
E) 1
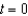 , distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as
, distilled water is added to the tank at a rate of 10 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as 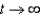 .
.A) 10
B) 26
C) 25
D) 0
E) 1

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
17
A 300-gallon tank is full of a solution containing 35 pounds of concentrate. Starting at time 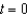 distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.
A)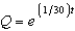
B)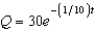
C)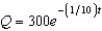
D)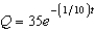
E)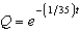
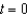 distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the amount of concentrate Q in the solution as a function of t.A)
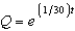
B)
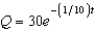
C)
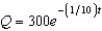
D)
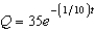
E)
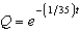

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck


