Deck 10: Introduction to Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/73
Play
Full screen (f)
Deck 10: Introduction to Differential Equations
1
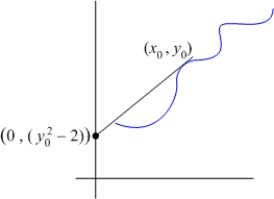
Find all the curves 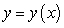 such that the tangent line at any point
such that the tangent line at any point 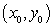 on the curve has a y-intercept equal to
on the curve has a y-intercept equal to 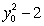 .
. 
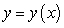 such that the tangent line at any point
such that the tangent line at any point 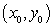 on the curve has a y-intercept equal to
on the curve has a y-intercept equal to 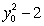 .
. 
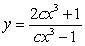
2
Solve the differential equation. 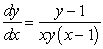
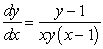
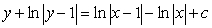
3
Solve the differential equation. 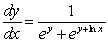
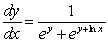
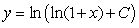
4
Consider the  circuit shown in the following figure.
circuit shown in the following figure. 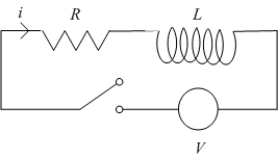 At
At 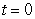 the switch is closed and the current passes through the circuit.
the switch is closed and the current passes through the circuit.
The constant voltage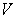 is the sum of the voltage
is the sum of the voltage 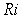 across the resistor and the voltage
across the resistor and the voltage 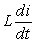 across the inductor.
across the inductor.
A) Set up an initial value problem satisfied by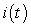 .
.
B) Solve for the current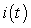 .
.
C) What is the current after a long time?
 circuit shown in the following figure.
circuit shown in the following figure.  At
At 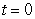 the switch is closed and the current passes through the circuit.
the switch is closed and the current passes through the circuit.The constant voltage
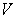 is the sum of the voltage
is the sum of the voltage 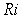 across the resistor and the voltage
across the resistor and the voltage 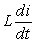 across the inductor.
across the inductor. A) Set up an initial value problem satisfied by
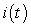 .
. B) Solve for the current
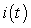 .
. C) What is the current after a long time?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the initial value problems.
A)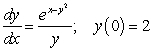
B)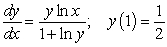
A)
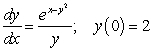
B)
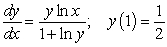

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the initial value problem. 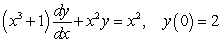
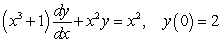

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
7
A certain chemical dissolves in water at a rate proportional to the product of the amount of chemical that had not yet been dissolved and the difference between its concentration in a saturated solution and its current concentration.
It is known that 100 g of the chemical are dissolved in 200 g of saturated solution. If 60 g of the chemical are added to 200 g of water, 20 g are dissolved in 2 h.
How many grams of the chemical are dissolved in 4 h?
It is known that 100 g of the chemical are dissolved in 200 g of saturated solution. If 60 g of the chemical are added to 200 g of water, 20 g are dissolved in 2 h.
How many grams of the chemical are dissolved in 4 h?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
8
An object of constant mass is projected away from the earth with initial velocity 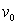 in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude
in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude 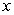 above the earth's surface, the velocity of the object satisfies the differential equation
above the earth's surface, the velocity of the object satisfies the differential equation 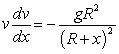 , where
, where 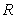 is the radius of the earth.
is the radius of the earth. 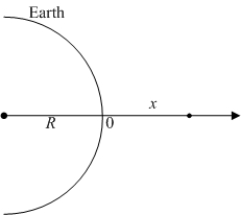
A) Solve for the velocity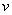 as a function of
as a function of 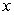 .
.
B) What is the maximum altitude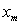 of the object if its initial velocity is
of the object if its initial velocity is 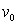 ?
?
C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth.
(Hint: find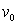 such that
such that 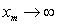 .)
.)
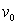 in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude
in a direction perpendicular to the earth's surface. Assuming there is no air resistance and considering the variation of the earth's gravitational field as a function of the altitude 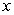 above the earth's surface, the velocity of the object satisfies the differential equation
above the earth's surface, the velocity of the object satisfies the differential equation 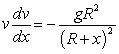 , where
, where 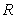 is the radius of the earth.
is the radius of the earth. 
A) Solve for the velocity
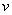 as a function of
as a function of 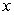 .
. B) What is the maximum altitude
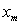 of the object if its initial velocity is
of the object if its initial velocity is 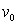 ?
? C) Find the escape velocity, that is, the least initial velocity for which the body will not return to the earth.
(Hint: find
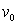 such that
such that 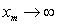 .)
.)
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the differential equations using separation of variables.
A)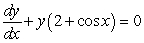
B)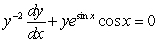
A)
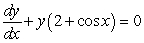
B)
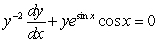

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
10
Find all the curves 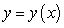 with the following property:
with the following property:
the y-intercept of the tangent line at any point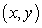 on the curve is equal to
on the curve is equal to 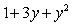 .
.
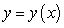 with the following property:
with the following property:the y-intercept of the tangent line at any point
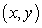 on the curve is equal to
on the curve is equal to 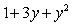 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
11
A conical tank filled with water has a height of 7 m and a top radius of 2 m. Water leaks through a hole of area 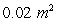 at the bottom.
at the bottom.
A) Find the water level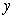 at time
at time 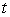 .
.
B) How long does it takes for the tank to empty?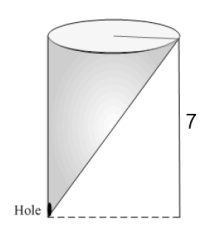
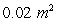 at the bottom.
at the bottom. A) Find the water level
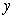 at time
at time 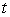 .
. B) How long does it takes for the tank to empty?


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the differential equations.
A)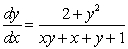
B)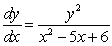 . (Hint: factor the denominator.)
. (Hint: factor the denominator.)
A)
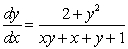
B)
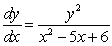 . (Hint: factor the denominator.)
. (Hint: factor the denominator.)
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
13
The horizontal cross sections at height  of a tank are discs of radius
of a tank are discs of radius  . The height of the tank is 10 m.
. The height of the tank is 10 m.
The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank.
How long does it take for the tank to empty?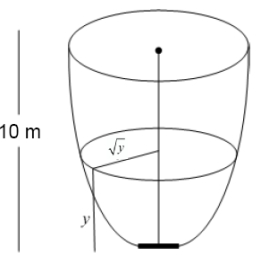
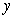 of a tank are discs of radius
of a tank are discs of radius 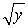 . The height of the tank is 10 m.
. The height of the tank is 10 m.The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank.
How long does it take for the tank to empty?


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the initial value problem. 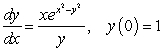
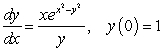

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
15
A water tank is obtained by rotating the graph of 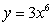 for
for 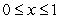 about the y-axis (assume length is measured in meters).
about the y-axis (assume length is measured in meters).
The tank is filled with water and water drains through a circular hole of radius
1 cm at the bottom of the tank.
How long does it take for the tank to empty?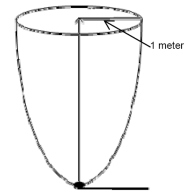
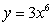 for
for 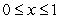 about the y-axis (assume length is measured in meters).
about the y-axis (assume length is measured in meters).The tank is filled with water and water drains through a circular hole of radius
1 cm at the bottom of the tank.
How long does it take for the tank to empty?


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the initial value problems.
A)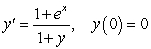
B)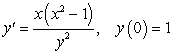
A)
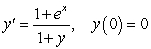
B)
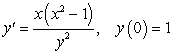

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
17
Find all curves 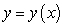 such that the tangent line at any point
such that the tangent line at any point 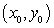 on the curve has a y-intercept that is equal to
on the curve has a y-intercept that is equal to 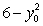 .
. 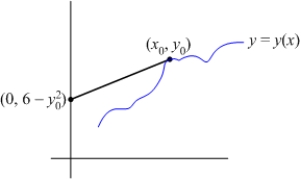
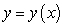 such that the tangent line at any point
such that the tangent line at any point 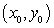 on the curve has a y-intercept that is equal to
on the curve has a y-intercept that is equal to 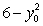 .
. 

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the initial value problem. 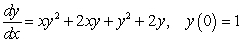
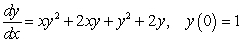

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the initial value problems.
A)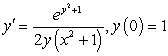
B)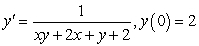
A)
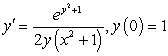
B)
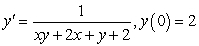

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
20
A tank in the shape of a prism and filled with water has a height of 5 m. The cross sections are equilateral triangles with a side of 1 m. Water leaks through a hole of area 0.01 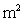 at the bottom of the tank.
at the bottom of the tank. 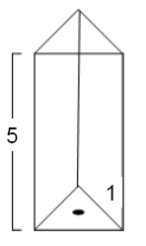
A) Find the water level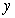 at time
at time 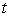 .
.
B) How long does it take for the tank to empty?
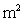 at the bottom of the tank.
at the bottom of the tank. 
A) Find the water level
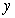 at time
at time 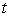 .
. B) How long does it take for the tank to empty?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
21
The graph of an increasing function 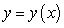 passes through the origin, and the arc length between the points
passes through the origin, and the arc length between the points 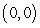 and
and 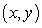 on the graph is
on the graph is 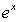 .
.
A) Write an initial value problem satisfied by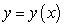 .
.
B) Use Euler's method with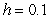 to estimate
to estimate 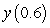 .
. 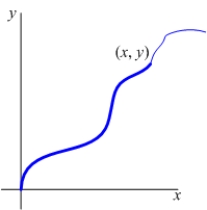
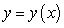 passes through the origin, and the arc length between the points
passes through the origin, and the arc length between the points 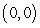 and
and 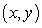 on the graph is
on the graph is 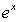 .
. A) Write an initial value problem satisfied by
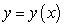 .
. B) Use Euler's method with
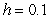 to estimate
to estimate 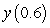 .
. 

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
22
Use Euler's method with 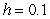 to approximate
to approximate 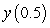 , where
, where 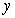 is the solution of the initial value problem
is the solution of the initial value problem 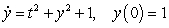 . Give your answer to five decimal places.
. Give your answer to five decimal places.
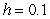 to approximate
to approximate 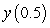 , where
, where 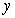 is the solution of the initial value problem
is the solution of the initial value problem 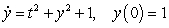 . Give your answer to five decimal places.
. Give your answer to five decimal places.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
23
Let 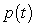 be the population of a certain animal species that satisfies the logistic equation
be the population of a certain animal species that satisfies the logistic equation 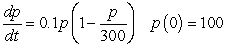 .
.
A) Find the equilibrium solutions and classify them.
B) What is the long-term behavior of the population?
C) Find the value of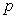 at the inflection point and explain its meaning referring to the population growth.
at the inflection point and explain its meaning referring to the population growth.
D) Solve the logistic equation and verify your answer to B.
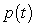 be the population of a certain animal species that satisfies the logistic equation
be the population of a certain animal species that satisfies the logistic equation 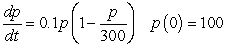 .
. A) Find the equilibrium solutions and classify them.
B) What is the long-term behavior of the population?
C) Find the value of
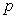 at the inflection point and explain its meaning referring to the population growth.
at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the logistic equation 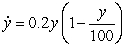 . The solution with the following initial condition is decreasing to minus infinity at a finite value of
. The solution with the following initial condition is decreasing to minus infinity at a finite value of 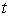 :
:
A)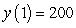
B)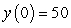
C)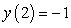
D)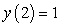
E) none of the above.
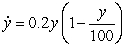 . The solution with the following initial condition is decreasing to minus infinity at a finite value of
. The solution with the following initial condition is decreasing to minus infinity at a finite value of 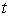 :
:A)
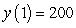
B)
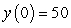
C)
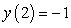
D)
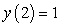
E) none of the above.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
25
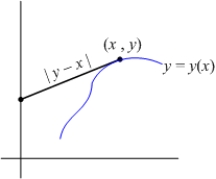
Let 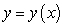 be an increasing function passing through
be an increasing function passing through 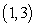 such that the length of the tangent line between the tangency point
such that the length of the tangent line between the tangency point 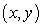 and the y-axis is
and the y-axis is 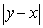 .
. 
A) Find an initial value problem satisfied by .
.
B) Use Euler's method with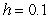 to approximate
to approximate 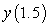 .
.
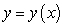 be an increasing function passing through
be an increasing function passing through 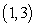 such that the length of the tangent line between the tangency point
such that the length of the tangent line between the tangency point 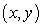 and the y-axis is
and the y-axis is 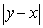 .
. 
A) Find an initial value problem satisfied by
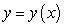 .
. B) Use Euler's method with
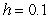 to approximate
to approximate 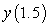 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
26
Use Euler's method with 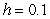 to approximate
to approximate 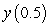 where
where 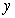 is the solution of
is the solution of 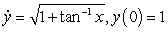 . Give your answer to five decimal places.
. Give your answer to five decimal places.
 to approximate
to approximate 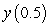 where
where 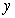 is the solution of
is the solution of 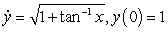 . Give your answer to five decimal places.
. Give your answer to five decimal places.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
27
Match the direction fields with their differential equations
A)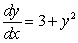
B)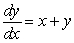
C)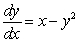
D)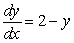
i)
ii)
iii)
iv)
A)
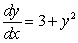
B)
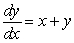
C)
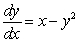
D)
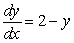
i)

ii)

iii)

iv)


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the initial value problem 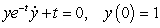 .
.
A) Use Euler's method with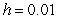 to approximate
to approximate 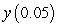 . Give your answer to six decimal places.
. Give your answer to six decimal places.
B) Solve the initial value problem and find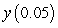 to six decimal places.
to six decimal places.
C) Compute the error in approximating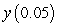 .
.
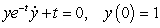 .
. A) Use Euler's method with
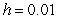 to approximate
to approximate 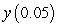 . Give your answer to six decimal places.
. Give your answer to six decimal places. B) Solve the initial value problem and find
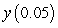 to six decimal places.
to six decimal places. C) Compute the error in approximating
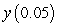 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
29
Use Euler's method with step size 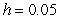 to approximate
to approximate 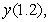 where
where 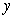 is the solution to the initial value problem
is the solution to the initial value problem 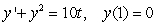 .
.
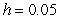 to approximate
to approximate 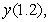 where
where 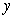 is the solution to the initial value problem
is the solution to the initial value problem 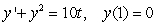 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
30
Use Euler's method with step size 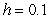 to approximate
to approximate 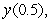 where
where 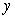 is the solution to the initial value problem
is the solution to the initial value problem 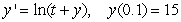 .
.
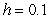 to approximate
to approximate 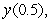 where
where 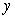 is the solution to the initial value problem
is the solution to the initial value problem 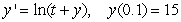 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the initial value problem 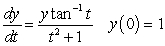 .
.
A) Use Euler's Method with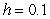 to approximate
to approximate 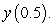
B) Use Euler's Method with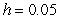 to approximate
to approximate 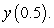
C) Solve the initial value problem and estimate the errors in parts A and B.
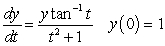 .
. A) Use Euler's Method with
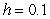 to approximate
to approximate 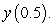
B) Use Euler's Method with
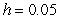 to approximate
to approximate 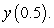
C) Solve the initial value problem and estimate the errors in parts A and B.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
32
Match the differential equation with its slope field.
A)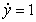
B)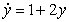
C)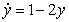
D)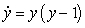
E)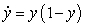
i)
ii)
iii)
iv)
v)
A)
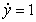
B)
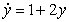
C)
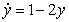
D)
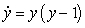
E)
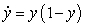
i)

ii)

iii)

iv)

v)


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the initial value problem 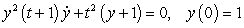 .
.
A) Use Euler's method with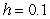 to approximate the solution at the point
to approximate the solution at the point 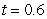 .
.
B) Solve the initial value problem and find the exact solution.
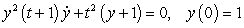 .
. A) Use Euler's method with
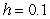 to approximate the solution at the point
to approximate the solution at the point 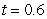 .
. B) Solve the initial value problem and find the exact solution.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
34
Use Euler's method with 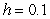 to approximate
to approximate 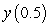 , where
, where 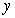 is the solution of the initial value problem
is the solution of the initial value problem 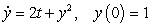 .
.
 to approximate
to approximate 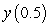 , where
, where 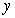 is the solution of the initial value problem
is the solution of the initial value problem 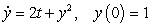 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
35
Which of the following graphs depicts possible solutions of a logistic equation?
A)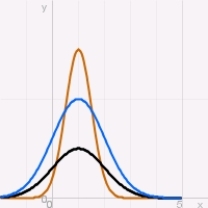
B)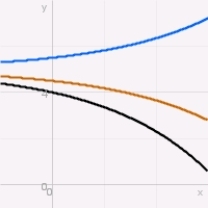
C)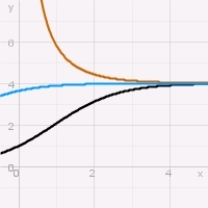
D)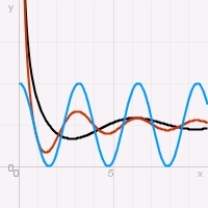
E) none of the above.
A)

B)

C)

D)

E) none of the above.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
36
Use Euler's method with step size 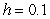 to approximate
to approximate 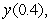 where
where 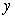 is the solution to the initial value problem
is the solution to the initial value problem 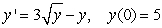 .
.
 to approximate
to approximate 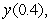 where
where 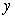 is the solution to the initial value problem
is the solution to the initial value problem 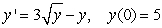 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
37
Match the differential equation with its slope field.
A)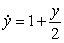
B)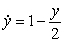
C)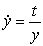
i) ii)
ii) 
iii)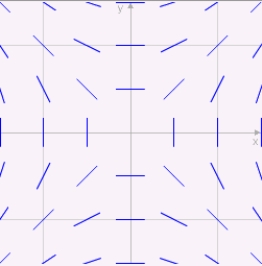
A)
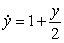
B)
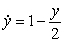
C)
i)
 ii)
ii) 
iii)


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the initial value problem 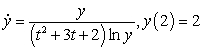
A) Use Euler's method with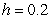 to approximate
to approximate 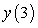 . Give your answer to five decimal places.
. Give your answer to five decimal places.
B) Solve the initial value problem and compute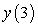 to five decimal places.
to five decimal places.
C) Compute the error in the approximation of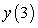 .
.
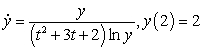
A) Use Euler's method with
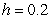 to approximate
to approximate 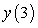 . Give your answer to five decimal places.
. Give your answer to five decimal places. B) Solve the initial value problem and compute
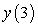 to five decimal places.
to five decimal places. C) Compute the error in the approximation of
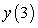 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the initial value problem. 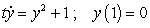 .
.
A) Use Euler's method with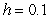 to approximate
to approximate 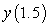 . Give your answer to six decimal places.
. Give your answer to six decimal places.
A) and
B) Use Euler's method with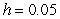 to approximate
to approximate 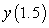 . Give your answer to six decimal places.
. Give your answer to six decimal places.
B).
C) Solve the initial value problem and estimate the error in parts
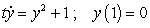 .
. A) Use Euler's method with
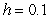 to approximate
to approximate 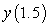 . Give your answer to six decimal places.
. Give your answer to six decimal places. A) and
B) Use Euler's method with
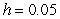 to approximate
to approximate 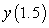 . Give your answer to six decimal places.
. Give your answer to six decimal places. B).
C) Solve the initial value problem and estimate the error in parts

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
40
Match the differential equation with its slope field
(A)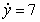 (B)
(B) 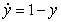 (C)
(C) 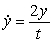 i)
i)  ii)
ii) 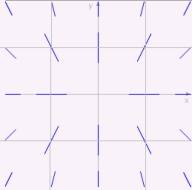 iii)
iii) 
(A)
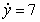 (B)
(B) 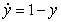 (C)
(C) 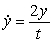 i)
i)  ii)
ii)  iii)
iii) 

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
41
Twenty-five rabbits were brought to a zoo 15 years ago.
At present there are 35 rabbits in the zoo. The zoo can support a maximum of 180 rabbits.
Assuming a logistic growth model, when will the rabbit population reach 50, 100, and 180 rabbits?
At present there are 35 rabbits in the zoo. The zoo can support a maximum of 180 rabbits.
Assuming a logistic growth model, when will the rabbit population reach 50, 100, and 180 rabbits?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
42
A rat population in a certain field is initially 500. After 3 years, the population increases to 700. Assuming logistic growth with a carrying capacity of 1000, how long after reaching 700 will it take for the population to reach 800?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
43
A deer population for a certain area is initially 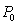 . After 6 years, the population increases to 250. After another 4 years, the population increases to 300. Assuming logistic growth with a carrying capacity of 400, what is
. After 6 years, the population increases to 250. After another 4 years, the population increases to 300. Assuming logistic growth with a carrying capacity of 400, what is 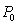 ?
?
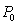 . After 6 years, the population increases to 250. After another 4 years, the population increases to 300. Assuming logistic growth with a carrying capacity of 400, what is
. After 6 years, the population increases to 250. After another 4 years, the population increases to 300. Assuming logistic growth with a carrying capacity of 400, what is 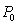 ?
?
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the initial value problem 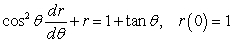 .
.
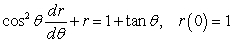 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
45
The differential equation 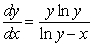 is:
is:
A) linear.
B) nonlinear, but it becomes linear if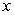 is the independent variable.
is the independent variable.
C) separable.
D) nonseparable, but it becomes separable if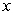 is the independent variable.
is the independent variable.
E) none of the above.
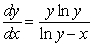 is:
is:A) linear.
B) nonlinear, but it becomes linear if
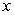 is the independent variable.
is the independent variable.C) separable.
D) nonseparable, but it becomes separable if
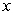 is the independent variable.
is the independent variable.E) none of the above.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
46
A deer population for a certain area was 400 at the beginning of the year 1995. After 2 years, the population increased to 500. Assuming logistic growth with a carrying capacity of 800, express the population as a function of t, the number of years since the beginning of 1995.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
47
A deer population for a certain area is initially 350. After 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 1200, how long after reaching 650 will it take the population to reach 1000?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
48
A deer population for a certain area is initially 500. After 3 years, the population increases to 600. Assuming logistic growth with a carrying capacity of 850, what is the deer population 2 years after the population reached 600?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
49
Thirty birds were brought to a zoo 10 years ago.
At present, there are 60 birds in the zoo. The zoo can support a maximum of 120 birds.
Assuming a logistic growth model, when will the bird population reach 80, 100, and 120 birds?
At present, there are 60 birds in the zoo. The zoo can support a maximum of 120 birds.
Assuming a logistic growth model, when will the bird population reach 80, 100, and 120 birds?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the linear equations.
A)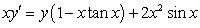
B)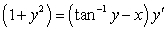 (Hint: rewrite for
(Hint: rewrite for 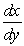 .)
.)
A)
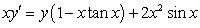
B)
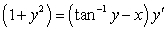 (Hint: rewrite for
(Hint: rewrite for 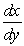 .)
.)
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
51
Twenty panda bears were brought to a national park 20 years ago. At present, there are 42 bears in the park. The park can support a maximum of 200 bears. Assuming a logistic growth model, when will the bear population reach 80, 150, and 200 bears?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
52
Let 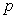 be a population of insects that is modeled by the logistic equation:
be a population of insects that is modeled by the logistic equation: 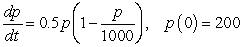
A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of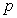 at the inflection point and explain its meaning referring to the population growth.
at the inflection point and explain its meaning referring to the population growth.
D) Solve the logistic equation and verify your answer to B.
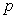 be a population of insects that is modeled by the logistic equation:
be a population of insects that is modeled by the logistic equation: 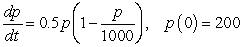
A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of
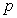 at the inflection point and explain its meaning referring to the population growth.
at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
53
Let 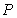 be the population of a certain animal species, satisfying the logistic equation
be the population of a certain animal species, satisfying the logistic equation 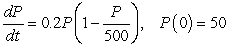
A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of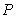 at the inflection point and explain its meaning referring to the population growth.
at the inflection point and explain its meaning referring to the population growth.
D) Solve the logistic equation and verify your answer to B.
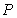 be the population of a certain animal species, satisfying the logistic equation
be the population of a certain animal species, satisfying the logistic equation 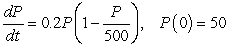
A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of
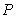 at the inflection point and explain its meaning referring to the population growth.
at the inflection point and explain its meaning referring to the population growth. D) Solve the logistic equation and verify your answer to B.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the following differential equations.
A)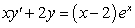
B)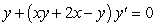 (Hint: rewrite for
(Hint: rewrite for 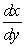 .)
.)
A)
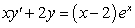
B)
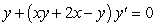 (Hint: rewrite for
(Hint: rewrite for 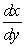 .)
.)
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
55
A rat population for a certain field is 300 at the beginning of the year 2002.. After 4 years, the population increased to 700. Assuming logistic growth with a carrying capacity of 900, express the population as a function of t, the number of years since the beginning of 2002.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
56
A rat population for a certain field is initially 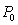 . After 3 years, the population increases to 450. After another 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 900, what is
. After 3 years, the population increases to 450. After another 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 900, what is 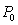 ?
?
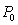 . After 3 years, the population increases to 450. After another 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 900, what is
. After 3 years, the population increases to 450. After another 2 years, the population increases to 650. Assuming logistic growth with a carrying capacity of 900, what is 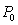 ?
?
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
57
A rat population in a certain field is initially 200. After 4 years, the population increases to 350. Assuming logistic growth with a carrying capacity of 550, what is the rat population 3 years after the population reached 350?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
58
Bees in a certain region are born at a rate that is proportional to their current population. Without any outside factors the population doubles in 3 weeks' time. It was observed that each day 12 bees joined the population, 10 were caught by men, and 5 died of natural causes.
Determine whether the population will survive if initially it counted 100 bees. If not, when will it die out?
Determine whether the population will survive if initially it counted 100 bees. If not, when will it die out?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
59
A 1200-gallon tank initially contains 500 gallons of water with 4 lbs of salt dissolved in it. Water with a salt concentration of 2 lbs/gal enters the tank at a rate of 10 gal/h, while the solution leaves the tank at a rate of 6 gal/h. Find the amount of salt in the tank when it overflows.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
60
Solving the differential equation 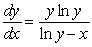 , we obtain the solution:
, we obtain the solution:
A)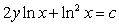 .
.
B)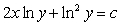 .
.
C)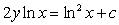 .
.
D)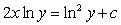 .
.
E)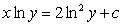 .
.
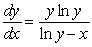 , we obtain the solution:
, we obtain the solution:A)
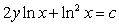 .
.B)
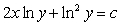 .
.C)
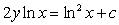 .
.D)
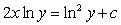 .
.E)
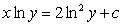 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
61
Deer in a certain region, are born at a rate that is proportional to their current population. With the absence of outside factors, the population will double in 3 years' time.
Each year 5 deer join the population, 10 are caught by hunters, and 4 die of natural causes.
If initially there are 50 deer, will the population survive? If not, when will it die out?
Each year 5 deer join the population, 10 are caught by hunters, and 4 die of natural causes.
If initially there are 50 deer, will the population survive? If not, when will it die out?

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
62
The curves orthogonal to the solutions of 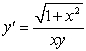 are:
are:
A)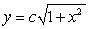 .
.
B)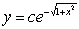 .
.
C)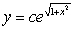 .
.
D)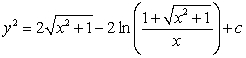 .
.
E) none of the above.
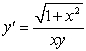 are:
are:A)
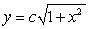 .
.B)
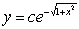 .
.C)
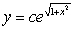 .
.D)
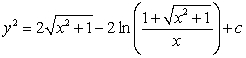 .
.E) none of the above.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the differential equation 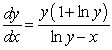 .
.
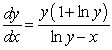 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the following equations.
A)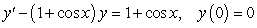
B)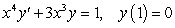
A)
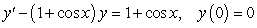
B)
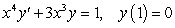

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
65
The differential equation 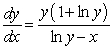 can be solved by which of the following?
can be solved by which of the following?
A) separating the variables
B) rewriting the equation with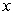 as the dependent variable and solving the linear equation
as the dependent variable and solving the linear equation
C) rewriting the equation with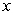 as the dependent variable and separating the variables
as the dependent variable and separating the variables
D) Euler's Method
E) none of the above
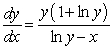 can be solved by which of the following?
can be solved by which of the following?A) separating the variables
B) rewriting the equation with
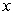 as the dependent variable and solving the linear equation
as the dependent variable and solving the linear equationC) rewriting the equation with
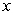 as the dependent variable and separating the variables
as the dependent variable and separating the variablesD) Euler's Method
E) none of the above

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
66
The differential equation 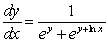 can be solved by which of the following?
can be solved by which of the following?
A) separating the variables
B) rewriting the equation with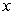 as the dependent variable and solving the linear equation
as the dependent variable and solving the linear equation
C) rewriting the equation with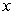 as the dependent variable and separating the variables
as the dependent variable and separating the variables
D) answers B and C are correct.
E) Euler's method.
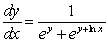 can be solved by which of the following?
can be solved by which of the following?A) separating the variables
B) rewriting the equation with
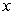 as the dependent variable and solving the linear equation
as the dependent variable and solving the linear equationC) rewriting the equation with
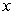 as the dependent variable and separating the variables
as the dependent variable and separating the variablesD) answers B and C are correct.
E) Euler's method.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
67
The differential equation 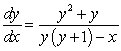 can be solved by which of the following?
can be solved by which of the following?
A) solving the linear equation - the equation is in the form of a linear equation
B) separating the variables
C) rewriting it with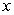 as the dependent variable and solving the resulting linear equation
as the dependent variable and solving the resulting linear equation
D) rewriting it with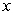 as the dependent variable and solving the resulting separable equation
as the dependent variable and solving the resulting separable equation
E) none of the above
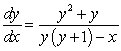 can be solved by which of the following?
can be solved by which of the following?A) solving the linear equation - the equation is in the form of a linear equation
B) separating the variables
C) rewriting it with
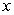 as the dependent variable and solving the resulting linear equation
as the dependent variable and solving the resulting linear equationD) rewriting it with
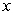 as the dependent variable and solving the resulting separable equation
as the dependent variable and solving the resulting separable equationE) none of the above

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the initial value problem 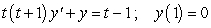 .
.
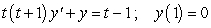 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the initial value problem 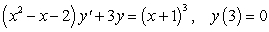 .
.
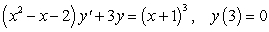 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
70
Use the following steps.
A) Write an equation for the areas using integrals.
B) Differentiate the equation in A and solve the resulting linear equation.
Ans:
A)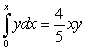 B)
B) 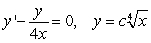
A pool contains 12 million gal of fresh water. Contaminated water flows into the pool at a rate of 4 million gal/year as the mixture in the pool flows out at the same rate.
The concentration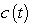 of the chemical in the incoming contaminated water is
of the chemical in the incoming contaminated water is 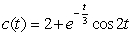 g/gal, where t is in years.
g/gal, where t is in years.
Find the amount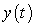 of the chemical in the pool at time
of the chemical in the pool at time 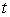 .
.
A) Write an equation for the areas using integrals.
B) Differentiate the equation in A and solve the resulting linear equation.
Ans:
A)
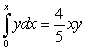 B)
B) 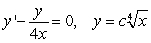
A pool contains 12 million gal of fresh water. Contaminated water flows into the pool at a rate of 4 million gal/year as the mixture in the pool flows out at the same rate.
The concentration
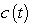 of the chemical in the incoming contaminated water is
of the chemical in the incoming contaminated water is 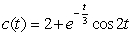 g/gal, where t is in years.
g/gal, where t is in years.Find the amount
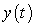 of the chemical in the pool at time
of the chemical in the pool at time 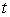 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
71
The curves orthogonal to the solutions of 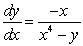 are:
are:
A)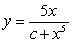 .
.
B)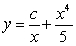 .
.
C)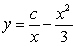 .
.
D)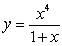 .
.
E) none of the above.
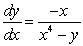 are:
are:A)
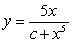 .
.B)
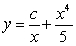 .
.C)
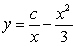 .
.D)
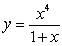 .
.E) none of the above.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the differential equation 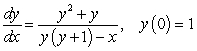 .
.
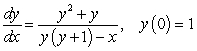 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the initial value problem 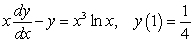 .
.
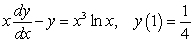 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck


