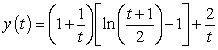Exam 10: Introduction to Differential Equations
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Thirty birds were brought to a zoo 10 years ago.
At present, there are 60 birds in the zoo. The zoo can support a maximum of 120 birds.
Assuming a logistic growth model, when will the bird population reach 80, 100, and 120 birds?
Free
(Essay)
4.9/5  (36)
(36)
Correct Answer:
80 birds: after 16.3 years
100 birds: after 24.6 years
120 birds: in the long term 
Consider the  circuit shown in the following figure.
circuit shown in the following figure. 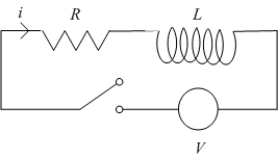 At
At 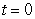 the switch is closed and the current passes through the circuit.
The constant voltage
the switch is closed and the current passes through the circuit.
The constant voltage 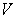 is the sum of the voltage
is the sum of the voltage 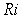 across the resistor and the voltage
across the resistor and the voltage 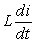 across the inductor.
A) Set up an initial value problem satisfied by
across the inductor.
A) Set up an initial value problem satisfied by 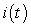 .
B) Solve for the current
.
B) Solve for the current 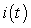 .
C) What is the current after a long time?
.
C) What is the current after a long time?
Free
(Essay)
4.9/5  (40)
(40)
Correct Answer:
A) 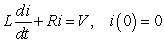 B)
B) 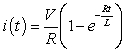 C)
C) 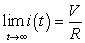
Consider the initial value problem 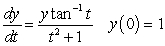 .
A) Use Euler's Method with
.
A) Use Euler's Method with 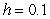 to approximate
to approximate 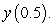 B) Use Euler's Method with
B) Use Euler's Method with 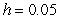 to approximate
to approximate 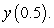 C) Solve the initial value problem and estimate the errors in parts A and B.
C) Solve the initial value problem and estimate the errors in parts A and B.
(Essay)
4.9/5  (41)
(41)
Let 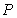 be the population of a certain animal species, satisfying the logistic equation
be the population of a certain animal species, satisfying the logistic equation 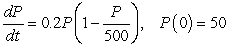 A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of
A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of 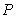 at the inflection point and explain its meaning referring to the population growth.
D) Solve the logistic equation and verify your answer to B.
at the inflection point and explain its meaning referring to the population growth.
D) Solve the logistic equation and verify your answer to B.
(Essay)
4.8/5  (37)
(37)
A rat population for a certain field is 300 at the beginning of the year 2002.. After 4 years, the population increased to 700. Assuming logistic growth with a carrying capacity of 900, express the population as a function of t, the number of years since the beginning of 2002.
(Essay)
4.9/5  (25)
(25)
A tank in the shape of a prism and filled with water has a height of 5 m. The cross sections are equilateral triangles with a side of 1 m. Water leaks through a hole of area 0.01 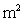 at the bottom of the tank.
at the bottom of the tank. 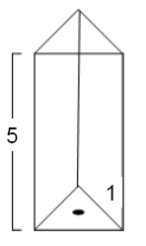 A) Find the water level
A) Find the water level 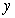 at time
at time 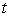 .
B) How long does it take for the tank to empty?
.
B) How long does it take for the tank to empty?
(Essay)
4.9/5  (35)
(35)
Use Euler's method with step size 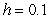 to approximate
to approximate 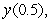 where
where 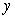 is the solution to the initial value problem
is the solution to the initial value problem 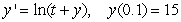 .
.
(Essay)
5.0/5  (34)
(34)
Use Euler's method with 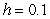 to approximate
to approximate 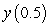 where
where 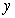 is the solution of
is the solution of 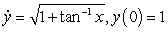 . Give your answer to five decimal places.
. Give your answer to five decimal places.
(Essay)
4.9/5  (40)
(40)
Use Euler's method with step size 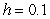 to approximate
to approximate 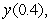 where
where 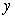 is the solution to the initial value problem
is the solution to the initial value problem 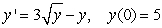 .
.
(Essay)
4.8/5  (30)
(30)
Find all the curves 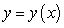 with the following property:
the y-intercept of the tangent line at any point
with the following property:
the y-intercept of the tangent line at any point 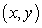 on the curve is equal to
on the curve is equal to 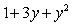 .
.
(Essay)
4.7/5  (27)
(27)
Consider the initial value problem 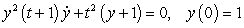 .
A) Use Euler's method with
.
A) Use Euler's method with 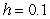 to approximate the solution at the point
to approximate the solution at the point 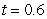 .
B) Solve the initial value problem and find the exact solution.
.
B) Solve the initial value problem and find the exact solution.
(Essay)
4.7/5  (34)
(34)
A conical tank filled with water has a height of 7 m and a top radius of 2 m. Water leaks through a hole of area 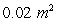 at the bottom.
A) Find the water level
at the bottom.
A) Find the water level 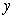 at time
at time 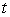 .
B) How long does it takes for the tank to empty?
.
B) How long does it takes for the tank to empty? 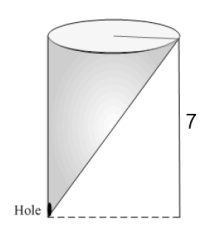
(Essay)
4.8/5  (38)
(38)
A deer population for a certain area was 400 at the beginning of the year 1995. After 2 years, the population increased to 500. Assuming logistic growth with a carrying capacity of 800, express the population as a function of t, the number of years since the beginning of 1995.
(Essay)
4.8/5  (36)
(36)
Solve the differential equations.
A) 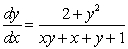 B)
B) 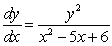 . (Hint: factor the denominator.)
. (Hint: factor the denominator.)
(Essay)
4.9/5  (33)
(33)
A rat population in a certain field is initially 500. After 3 years, the population increases to 700. Assuming logistic growth with a carrying capacity of 1000, how long after reaching 700 will it take for the population to reach 800?
(Short Answer)
4.9/5  (34)
(34)
Use Euler's method with 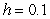 to approximate
to approximate 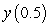 , where
, where 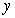 is the solution of the initial value problem
is the solution of the initial value problem 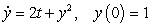 .
.
(Essay)
4.8/5  (34)
(34)
Showing 1 - 20 of 73
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)