Deck 2: Limits
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/97
Play
Full screen (f)
Deck 2: Limits
1
Determine the one-sided limits at 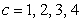 of the function shown in the figure and state whether the limit exists at these points.
of the function shown in the figure and state whether the limit exists at these points. 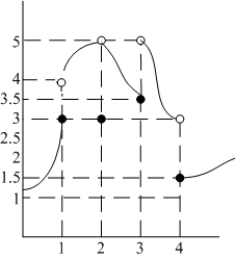
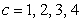 of the function shown in the figure and state whether the limit exists at these points.
of the function shown in the figure and state whether the limit exists at these points. 
Left-sided
Right-sided
Limit
1
3
4
Does not exist
2
5
5
Exists (5)
3
3.5
5
Does not exist
4
3
1.5
Does not exist
Right-sided
Limit
1
3
4
Does not exist
2
5
5
Exists (5)
3
3.5
5
Does not exist
4
3
1.5
Does not exist
2
Let 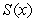 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 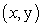 on the graph of the equation
on the graph of the equation 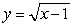 . Calculate the average rate of change of
. Calculate the average rate of change of 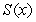 for
for 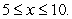
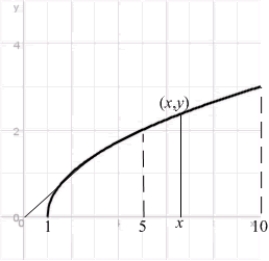
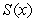 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 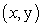 on the graph of the equation
on the graph of the equation 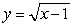 . Calculate the average rate of change of
. Calculate the average rate of change of 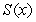 for
for 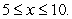

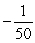
3
The electrical field due to an infinite rod at a point at distance 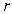 from the rod is perpendicular to the rod and has a magnitude of
from the rod is perpendicular to the rod and has a magnitude of 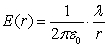 (
( 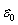 is a constant and
is a constant and 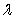 is the longitudinal charge density).
is the longitudinal charge density).
Find the average rate of change of the field along the interval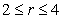 .
. 
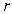 from the rod is perpendicular to the rod and has a magnitude of
from the rod is perpendicular to the rod and has a magnitude of 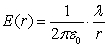 (
( 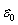 is a constant and
is a constant and 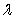 is the longitudinal charge density).
is the longitudinal charge density).Find the average rate of change of the field along the interval
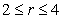 .
. 
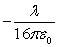
4
The volume of a sphere of radius 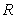 is
is 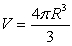 . What is the average rate of change of the volume when the radius increases from
. What is the average rate of change of the volume when the radius increases from 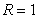 to
to 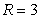 ?
?
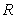 is
is 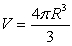 . What is the average rate of change of the volume when the radius increases from
. What is the average rate of change of the volume when the radius increases from 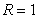 to
to 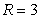 ?
?
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
5
Determine the one-sided limits at 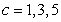 of the function
of the function 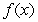 shown in the figure and state whether the limit exists at these points.
shown in the figure and state whether the limit exists at these points. 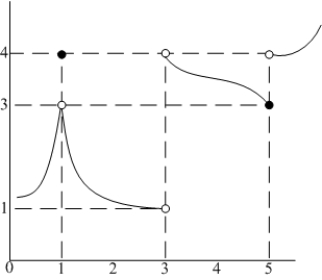
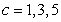 of the function
of the function  shown in the figure and state whether the limit exists at these points.
shown in the figure and state whether the limit exists at these points. 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
6
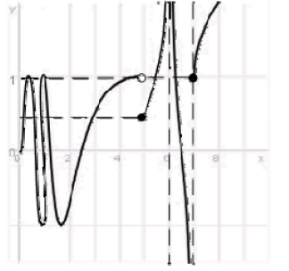
The graph of a function 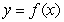 is shown in the figure.
is shown in the figure.
Determine the following limits or state that the limit does not exist (if the limit is infinite, write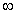 or
or 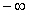 :
: 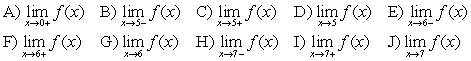
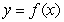 is shown in the figure.
is shown in the figure.Determine the following limits or state that the limit does not exist (if the limit is infinite, write
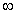 or
or 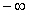 :
: 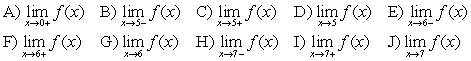


Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
7
Let 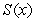 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 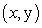 on the graph of the semi-ellipse
on the graph of the semi-ellipse 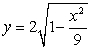 . Calculate the average rate of change of
. Calculate the average rate of change of 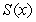 for
for 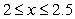

 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 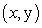 on the graph of the semi-ellipse
on the graph of the semi-ellipse 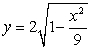 . Calculate the average rate of change of
. Calculate the average rate of change of 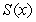 for
for 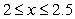



Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
8
Let 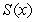 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 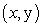 on the graph of the equation
on the graph of the equation 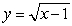 . Calculate the average rate of change of
. Calculate the average rate of change of 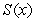 for
for 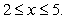
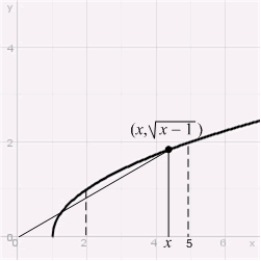
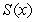 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 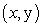 on the graph of the equation
on the graph of the equation 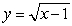 . Calculate the average rate of change of
. Calculate the average rate of change of 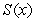 for
for 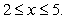


Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
9
Determine the one-sided limits at 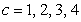 of the function shown in the figure and state whether the limit exists at these points.
of the function shown in the figure and state whether the limit exists at these points. 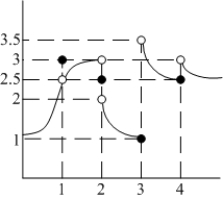
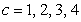 of the function shown in the figure and state whether the limit exists at these points.
of the function shown in the figure and state whether the limit exists at these points. 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
10
Determine 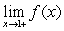 and
and 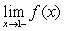 for the function shown in the figure.
for the function shown in the figure. 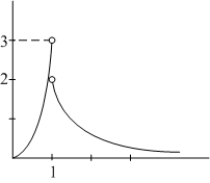
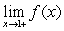 and
and 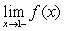 for the function shown in the figure.
for the function shown in the figure. 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the function 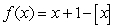 for
for 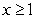 .
.
A) Write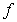 in piecewise form. What is
in piecewise form. What is 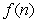 for positive integers
for positive integers 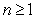 ?
?
B) Find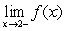 and
and 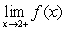 .
.
C) For which values of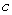 does the limit
does the limit 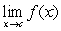 fail to exist?
fail to exist? 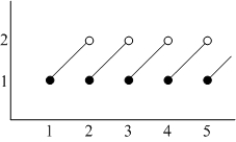
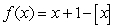 for
for 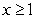 .
. A) Write
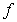 in piecewise form. What is
in piecewise form. What is 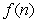 for positive integers
for positive integers 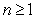 ?
? B) Find
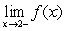 and
and 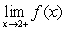 .
. C) For which values of
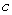 does the limit
does the limit 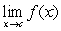 fail to exist?
fail to exist? 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
12
The flight-time of a shell shot at an angle 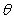 and initial velocity
and initial velocity 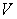 is
is 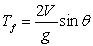 . Compute the average rate of change of the flight time for
. Compute the average rate of change of the flight time for 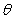 in the interval
in the interval 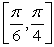 .
.
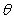 and initial velocity
and initial velocity 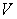 is
is 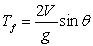 . Compute the average rate of change of the flight time for
. Compute the average rate of change of the flight time for 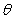 in the interval
in the interval 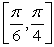 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the function 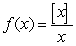 for
for 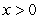 .
.
A) Write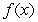 in piecewise form.
in piecewise form.
What is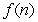 for positive integers
for positive integers 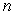 ?
?
B) Determine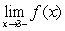 and
and 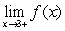 .
.
C) For which values of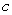 does
does 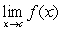 exist?
exist? 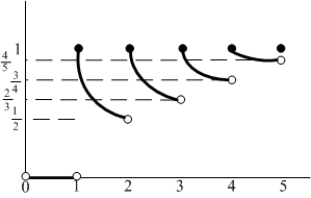
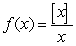 for
for 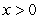 .
. A) Write
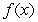 in piecewise form.
in piecewise form.What is
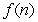 for positive integers
for positive integers 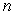 ?
? B) Determine
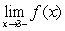 and
and 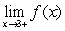 .
. C) For which values of
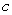 does
does 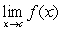 exist?
exist? 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
14
A balloon is blown up and takes the shape of a sphere. What is the average rate of change of the surface area of the balloon as the radius increases from 3 cm to 4 cm?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
15
The electrical field caused by an electrical charge 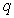 at a point at distance
at a point at distance 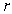 is
is 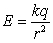 (
( 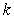 is a constant).
is a constant).
Find the average rate of change of the field along the interval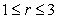 .
.
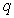 at a point at distance
at a point at distance 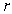 is
is 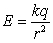 (
( 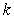 is a constant).
is a constant).Find the average rate of change of the field along the interval
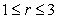 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
16
The position of a particle is given by 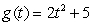 . Compute the average velocity over the time interval
. Compute the average velocity over the time interval 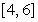 . Estimate the instantaneous velocity at
. Estimate the instantaneous velocity at 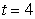 .
.
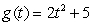 . Compute the average velocity over the time interval
. Compute the average velocity over the time interval 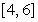 . Estimate the instantaneous velocity at
. Estimate the instantaneous velocity at 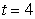 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
17
Let 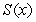 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 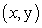 on the graph of the equation
on the graph of the equation 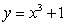 . Calculate the average rate of change of
. Calculate the average rate of change of  for
for 

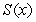 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 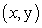 on the graph of the equation
on the graph of the equation 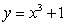 . Calculate the average rate of change of
. Calculate the average rate of change of 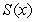 for
for 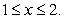



Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
18
The volume of a cone of radius 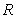 and height
and height 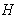 is
is 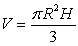 .
.
What is the average rate of change of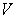 if the radius increases from 1 to 3 and the height remains unchanged?
if the radius increases from 1 to 3 and the height remains unchanged?
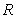 and height
and height 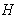 is
is 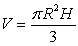 .
.What is the average rate of change of
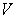 if the radius increases from 1 to 3 and the height remains unchanged?
if the radius increases from 1 to 3 and the height remains unchanged?
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
19
The greatest integer function is defined by 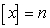 , where
, where 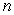 is the unique integer such that
is the unique integer such that 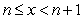 .
.
The graph of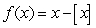 is shown in the figure.
is shown in the figure.
A) For which values of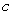 does
does 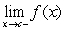 exist?
exist?
B) For which values of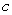 does
does 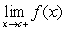 exist?
exist?
C) For which values of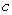 does
does 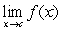 exist?
exist? 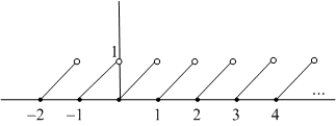
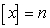 , where
, where 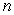 is the unique integer such that
is the unique integer such that 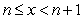 .
.The graph of
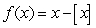 is shown in the figure.
is shown in the figure. A) For which values of
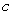 does
does 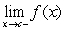 exist?
exist? B) For which values of
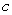 does
does 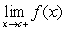 exist?
exist? C) For which values of
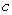 does
does 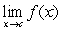 exist?
exist? 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
20
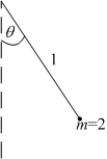
The potential energy 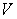 of a pendulum of length 1 and mass 2, relative to its rest position is
of a pendulum of length 1 and mass 2, relative to its rest position is 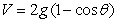 .
.
Compute the average rate of change of the potential energy over the angle interval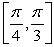 .
. 
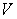 of a pendulum of length 1 and mass 2, relative to its rest position is
of a pendulum of length 1 and mass 2, relative to its rest position is 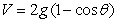 .
.Compute the average rate of change of the potential energy over the angle interval
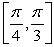 .
. 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
21
Let 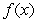 ,
, 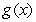 , and
, and 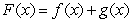 . To prove that if
. To prove that if 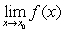 and
and 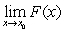 exist then also
exist then also 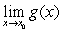 exists, we should use:
exists, we should use:
A) The Product Rule applied to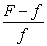 and
and 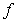 .
.
B) The Quotient Rule applied to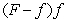 and
and 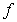 .
.
C) The Sum Rule applied to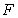 and
and 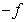 .
.
D) The statement is not true.
E) A and C are correct.
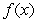 ,
, 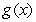 , and
, and 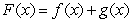 . To prove that if
. To prove that if 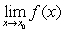 and
and 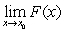 exist then also
exist then also 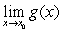 exists, we should use:
exists, we should use:A) The Product Rule applied to
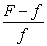 and
and 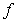 .
.B) The Quotient Rule applied to
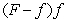 and
and 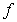 .
.C) The Sum Rule applied to
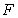 and
and  .
.D) The statement is not true.
E) A and C are correct.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
22
Let 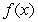 ,
, 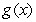 be functions and let
be functions and let 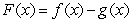 . Consider the following statement:
. Consider the following statement:
If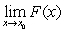 and
and 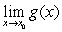 exist then also
exist then also 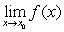 exists.
exists.
To prove this statement we should use:
A) The statement is not true.
B) The Product Rule applied to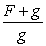 and
and 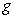 .
.
C) The Quotient Rule applied to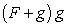 and
and 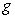 .
.
D) The Sum Rule applied to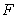 and
and 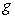 .
.
E) None of the above.
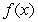 ,
, 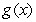 be functions and let
be functions and let 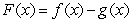 . Consider the following statement:
. Consider the following statement:If
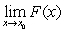 and
and 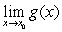 exist then also
exist then also 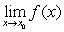 exists.
exists.To prove this statement we should use:
A) The statement is not true.
B) The Product Rule applied to
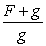 and
and 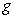 .
.C) The Quotient Rule applied to
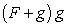 and
and 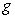 .
.D) The Sum Rule applied to
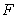 and
and 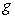 .
.E) None of the above.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the limits using the Limit Laws:
A)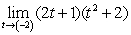
B)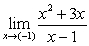
C)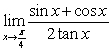
D)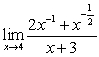
A)
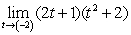
B)
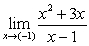
C)
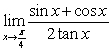
D)
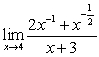

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
24
If 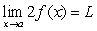 and
and 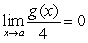 , calculate the following limits if possible. If not, state not possible. Assume
, calculate the following limits if possible. If not, state not possible. Assume 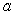 and
and 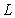 are nonzero real numbers.
are nonzero real numbers.
A)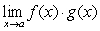
B)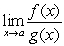
C)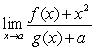
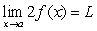 and
and 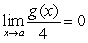 , calculate the following limits if possible. If not, state not possible. Assume
, calculate the following limits if possible. If not, state not possible. Assume 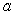 and
and 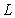 are nonzero real numbers.
are nonzero real numbers. A)
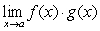
B)
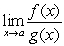
C)
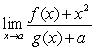

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following functions are examples of the existence of the limit 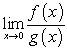 , although the limits of
, although the limits of 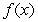 and
and 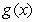 as
as 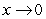 do not exist.
do not exist.
A)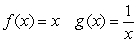
B)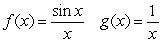
C)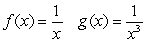
D)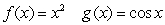
E)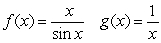
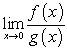 , although the limits of
, although the limits of 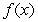 and
and 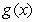 as
as 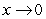 do not exist.
do not exist.A)
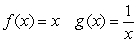
B)
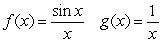
C)
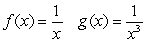
D)
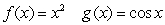
E)
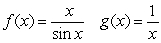

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the limits using the Limit Laws:
A)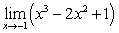
B)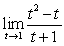
C)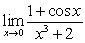
D)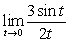
A)
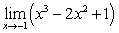
B)
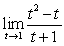
C)
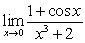
D)
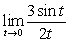

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
27
Compute the following one-sided limits:
A)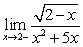
B)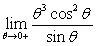
C)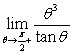
A)
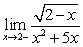
B)
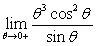
C)
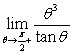

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
28
Determine the points at which the following functions are not continuous and state the type of discontinuity: removable, jump, infinite, or none of these.
A)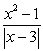
B)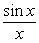
C)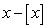
D)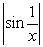
A)
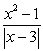
B)
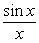
C)
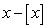
D)
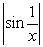

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
29
Find the values of 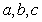 which make the function continuous:
which make the function continuous: 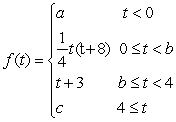
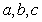 which make the function continuous:
which make the function continuous: 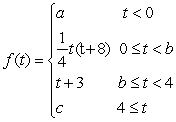

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the limits using the Limit Laws:
A)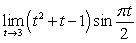
B)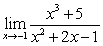

C)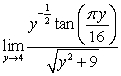
A)
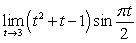
B)
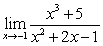

C)
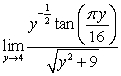

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the limits using the Limit Laws:
A)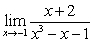
B)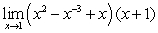
C)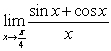
A)
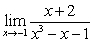
B)
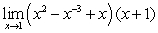
C)
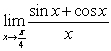

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
32
Determine whether the function is left or right continuous at the points of discontinuity:
A)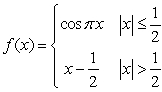
B)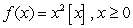
A)
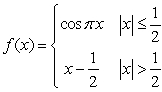
B)
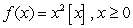

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
33
At each point of discontinuity state whether the function is left or right continuous: 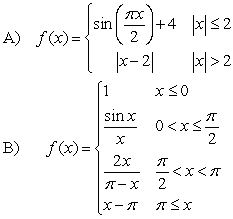
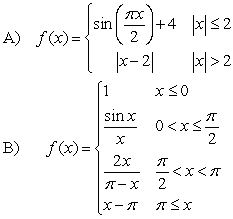

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
34
Let 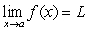 . Determine whether each of the following statements is always true, never true, or sometimes true.
. Determine whether each of the following statements is always true, never true, or sometimes true.
A)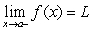
B)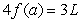
C)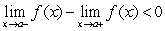
D)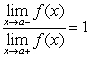
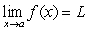 . Determine whether each of the following statements is always true, never true, or sometimes true.
. Determine whether each of the following statements is always true, never true, or sometimes true. A)
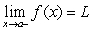
B)
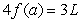
C)
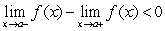
D)
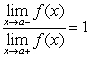

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
35
If 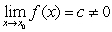 and
and 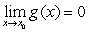 then
then 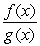 does not converge to a finite limit as
does not converge to a finite limit as 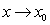 .
.
For proving, we assume that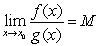 exists and is finite. Then
exists and is finite. Then
By the Quotient Rule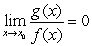 and by the Product Rule
and by the Product Rule 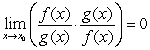 .
.
Which of the statements below completes the proof?
A) From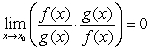 , it follows that 1=0, which is a contradiction.
, it follows that 1=0, which is a contradiction.
B) From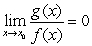 , we can conclude that
, we can conclude that 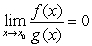 , which contradicts our assumption.
, which contradicts our assumption.
C) From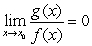 , we can conclude that
, we can conclude that 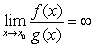 , which contradicts our assumption.
, which contradicts our assumption.
D) From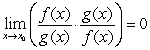 , we can conclude that
, we can conclude that 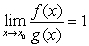 , which contradicts our assumption.
, which contradicts our assumption.
E) A and C are correct.
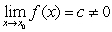 and
and 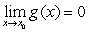 then
then 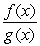 does not converge to a finite limit as
does not converge to a finite limit as 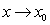 .
.For proving, we assume that
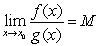 exists and is finite. Then
exists and is finite. ThenBy the Quotient Rule
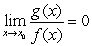 and by the Product Rule
and by the Product Rule 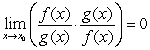 .
.Which of the statements below completes the proof?
A) From
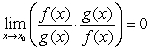 , it follows that 1=0, which is a contradiction.
, it follows that 1=0, which is a contradiction.B) From
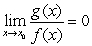 , we can conclude that
, we can conclude that 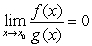 , which contradicts our assumption.
, which contradicts our assumption.C) From
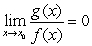 , we can conclude that
, we can conclude that 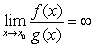 , which contradicts our assumption.
, which contradicts our assumption.D) From
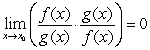 , we can conclude that
, we can conclude that 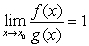 , which contradicts our assumption.
, which contradicts our assumption.E) A and C are correct.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
36
Find the points of discontinuity and state their type
A)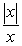
B)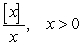
C)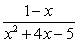
A)
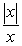
B)
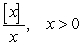
C)
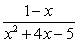

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
37
The following functions are examples of the existence of the limit 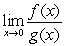 although the limits
although the limits 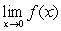 and
and 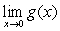 do not exist.
do not exist.
A)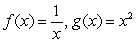
B)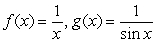
C)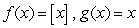
D)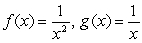
E)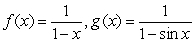
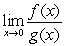 although the limits
although the limits 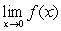 and
and 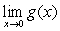 do not exist.
do not exist.A)
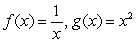
B)
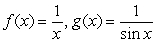
C)
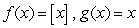
D)
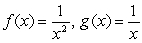
E)
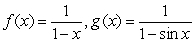

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
38
Determine whether the following statement is correct. If yes, prove it; otherwise give a counterexample
If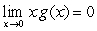 , then
, then 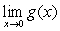 exists.
exists.
If
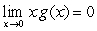 , then
, then 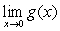 exists.
exists.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
39
Find 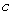 such that
such that 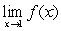 exists and compute the limit
exists and compute the limit 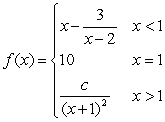
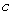 such that
such that 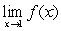 exists and compute the limit
exists and compute the limit 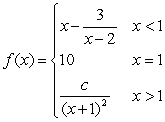

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
40
Let 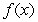 be the following function defined for
be the following function defined for 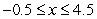 :
: 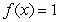 where
where 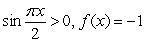 where
where 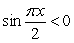 and
and 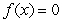 where
where 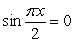 .
.
Write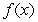 piecewise, sketch its graph, and determine the points where the limit of
piecewise, sketch its graph, and determine the points where the limit of 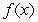 does not exist. Find the one-sided limits at these points.
does not exist. Find the one-sided limits at these points.
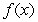 be the following function defined for
be the following function defined for 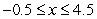 :
: 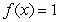 where
where 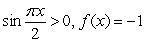 where
where 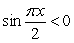 and
and 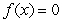 where
where 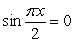 .
.Write
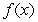 piecewise, sketch its graph, and determine the points where the limit of
piecewise, sketch its graph, and determine the points where the limit of 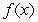 does not exist. Find the one-sided limits at these points.
does not exist. Find the one-sided limits at these points.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
41
At each point of discontinuity state whether the function is left or right continuous.
A)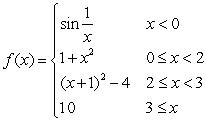
B)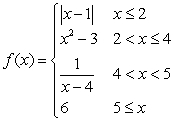
A)
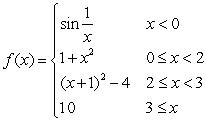
B)
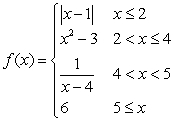

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the limit or state that it does not exist
A)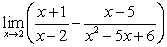
B)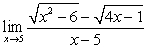
C)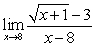
A)
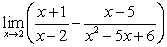
B)
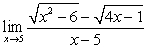
C)
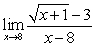

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
43
Find the values of 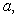
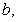 and
and 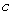 which make the following function continuous:
which make the following function continuous: 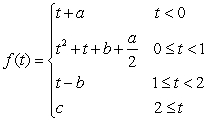
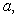
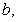 and
and 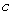 which make the following function continuous:
which make the following function continuous: 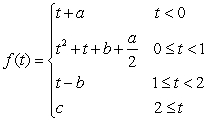

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
44
Find the value of 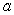 for which the limit exists and compute the limit
for which the limit exists and compute the limit 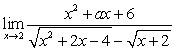
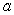 for which the limit exists and compute the limit
for which the limit exists and compute the limit 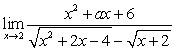

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the limit 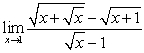
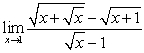

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate the limit or state that it does not exist
A)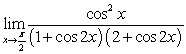
B)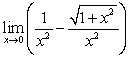
C)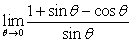
A)
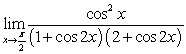
B)
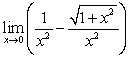
C)
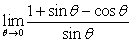

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
47
Sketch the graph of a function 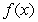 that satisfies
that satisfies 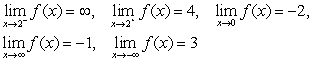
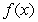 that satisfies
that satisfies 

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
48
Let 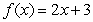 Find .
Find . 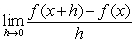 at
at 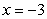 .
.
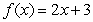 Find .
Find . 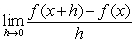 at
at 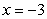 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the limit or state that it does not exist
A)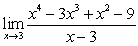
B)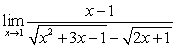
C)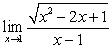
A)
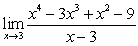
B)
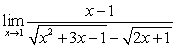
C)
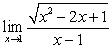

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
50
Determine the value of 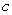 for which the limit exists and find the limit
for which the limit exists and find the limit 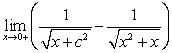
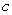 for which the limit exists and find the limit
for which the limit exists and find the limit 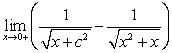

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
51
Find the constants 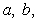 and
and 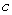 which make the function continuous:
which make the function continuous: 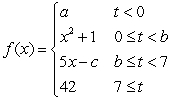
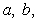 and
and 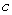 which make the function continuous:
which make the function continuous: 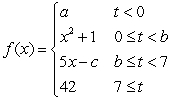

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the limit or state that it does not exist
A)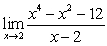
B)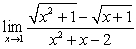
C)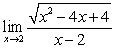
A)
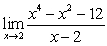
B)
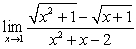
C)
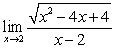

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
53
At each point of discontinuity state whether the function is left continuous, right continuous, or neither
A)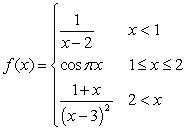
B)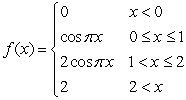
A)
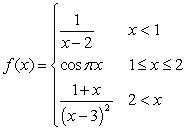
B)
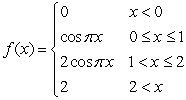

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the limits in terms of the constants involved
A)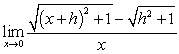
B)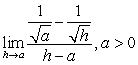
A)
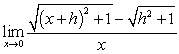
B)
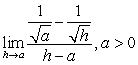

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
55
Find all values of 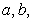 and
and 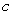 which make the following function continuous:
which make the following function continuous: 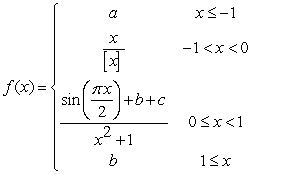
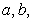 and
and 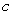 which make the following function continuous:
which make the following function continuous: 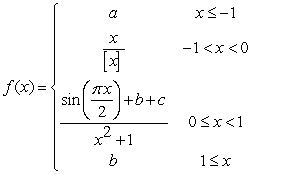

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
56
Let 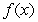 be the following function:
be the following function: 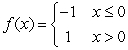 The function
The function 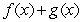 is continuous for the following function
is continuous for the following function 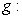
A)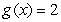 if
if 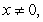
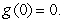 .
.
B)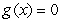 if
if 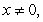
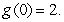
C)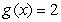 if
if 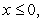
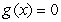 if
if 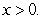
D)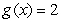 if
if 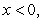
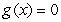 if
if 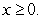
E) A and C are correct.
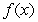 be the following function:
be the following function: 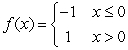 The function
The function 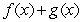 is continuous for the following function
is continuous for the following function 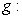
A)
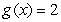 if
if 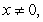
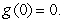 .
.B)
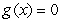 if
if 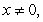
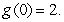
C)
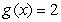 if
if 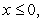
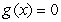 if
if 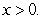
D)
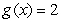 if
if 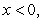
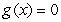 if
if 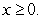
E) A and C are correct.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
57
Determine the points where the function is not continuous and state the type of discontinuity: removable, jump, infinite, or none of these:
A)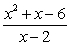
B)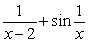
C)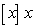
D)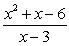
A)
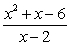
B)
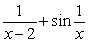
C)
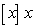
D)
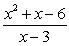

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
58
Let 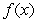 be a discontinuous function. Can you find a continuous function
be a discontinuous function. Can you find a continuous function 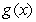 such that
such that 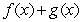 is continuous? Explain.
is continuous? Explain.
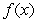 be a discontinuous function. Can you find a continuous function
be a discontinuous function. Can you find a continuous function 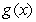 such that
such that 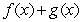 is continuous? Explain.
is continuous? Explain.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the limit or state that it does not exist
A)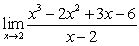
B)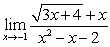
C)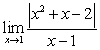
A)
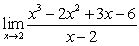
B)
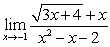
C)
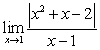

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
60
Determine the points where the function is not continuous and state the type of the discontinuity: removable, jump, infinite, or none of these.
A)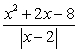
B)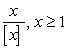
C)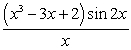
A)
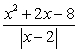
B)
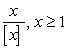
C)
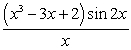

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
61
Use the Squeeze Theorem to evaluate the limit 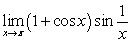
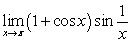

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
62
Compute the following limits:
A)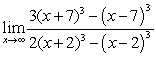
B)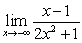
C)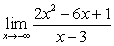
A)
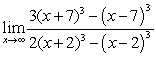
B)
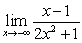
C)
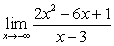

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
63
Show that 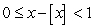 for all
for all 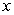 .
.
Use the above inequality and the Squeeze Theorem to evaluate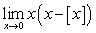 .
.
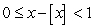 for all
for all 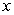 .
.Use the above inequality and the Squeeze Theorem to evaluate
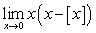 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
64
Calculate the following limits:
A)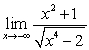

B)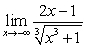
C)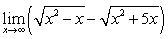
A)
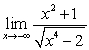

B)
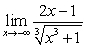
C)
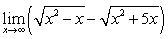

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
65
Find 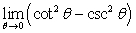 .
.
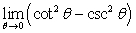 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
66
Calculate the limits
A)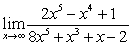
B)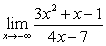
C)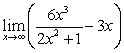
A)
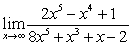
B)
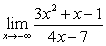
C)
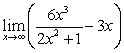

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the limits
A)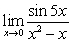 (Hint: Factor the denominator)
(Hint: Factor the denominator)
B)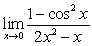 (Hint: Factor the two expressions)
(Hint: Factor the two expressions)
C)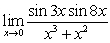
A)
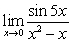 (Hint: Factor the denominator)
(Hint: Factor the denominator) B)
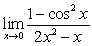 (Hint: Factor the two expressions)
(Hint: Factor the two expressions) C)
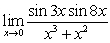

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
68
True/False:
If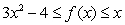 on the interval
on the interval 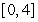 then
then 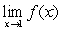 must exist
must exist
If
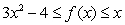 on the interval
on the interval 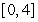 then
then 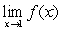 must exist
must exist
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate the limit or state that it does not exist
A)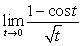
B)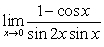
C)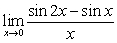
A)
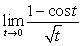
B)
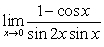
C)
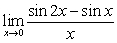

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the limits using the Squeeze Theorem, trigonometric identities, and trigonometric limits as necessary
A)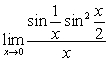
B)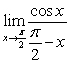
C)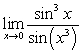
A)
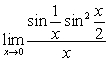
B)
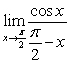
C)
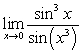

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
71
Compute the following limits:
A)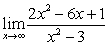
B)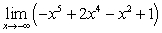
C)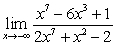
A)
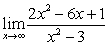
B)
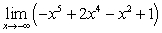
C)
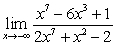

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
72
Compute the following limits:
A)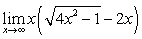
(Hint: Multiply and divide by the conjugate expression.)
B)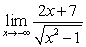
(Hint: For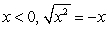 .)
.)
C)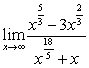
A)
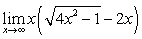
(Hint: Multiply and divide by the conjugate expression.)
B)
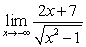
(Hint: For
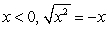 .)
.) C)
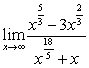

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
73
Compute the following limits:
A)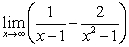
B)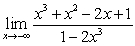
C)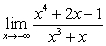
A)
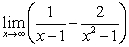
B)
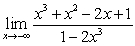
C)
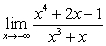

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
74
Calculate the limits:
A)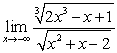
B)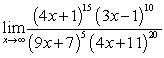
C)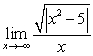
A)
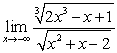
B)
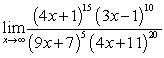
C)
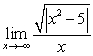

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
75
Evaluate the limits in terms of the constants involved
A)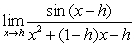
B)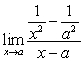
A)
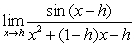
B)
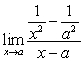

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
76
Show that 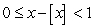 for all
for all 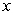 . Use the Squeeze Theorem to evaluate
. Use the Squeeze Theorem to evaluate 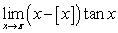 .
.
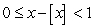 for all
for all 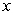 . Use the Squeeze Theorem to evaluate
. Use the Squeeze Theorem to evaluate 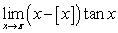 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
77
Find the value of 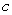 such that the following limit exists, and evaluate the limit for this value:
such that the following limit exists, and evaluate the limit for this value: 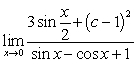
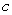 such that the following limit exists, and evaluate the limit for this value:
such that the following limit exists, and evaluate the limit for this value: 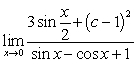

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate the limits
A)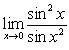
B)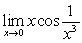
C)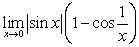
A)
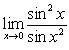
B)
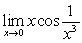
C)
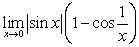

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate the limits
A)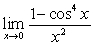
B)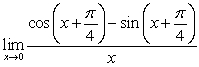
A)
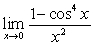
B)
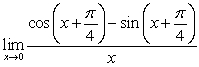

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
80
Find 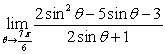 .
.
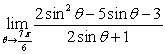 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck


