Exam 2: Limits
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Evaluate the limits using the Limit Laws:
A) 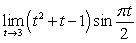 B)
B) 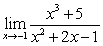
 C)
C) 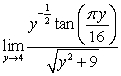
Free
(Essay)
4.7/5  (37)
(37)
Correct Answer:
A) 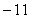 B)
B) 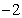 C)
C) 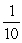
Evaluate the limit or state that it does not exist
A) 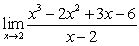 B)
B) 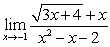 C)
C) 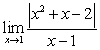
Free
(Essay)
4.8/5  (29)
(29)
Correct Answer:
A) 7
B) 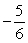 C) Limit does not exist
C) Limit does not exist
Determine the points where the function is not continuous and state the type of the discontinuity: removable, jump, infinite, or none of these.
A) 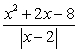 B)
B) 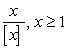 C)
C) 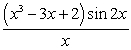
Free
(Essay)
4.9/5  (32)
(32)
Correct Answer:
A) 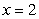 , jump
, jump
B) 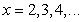 , jump
, jump
C) 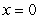 , removable
, removable
Find 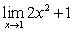 and use the formal definition of the limit to rigorously prove your result.
and use the formal definition of the limit to rigorously prove your result.
(Essay)
4.7/5  (35)
(35)
Determine the points where the function is not continuous and state the type of discontinuity: removable, jump, infinite, or none of these:
A) 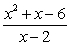 B)
B) 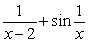 C)
C) 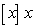 D)
D) 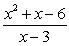
(Essay)
4.8/5  (36)
(36)
The greatest integer function is defined by 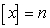 , where
, where 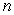 is the unique integer such that
is the unique integer such that 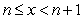 .
The graph of
.
The graph of 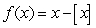 is shown in the figure.
A) For which values of
is shown in the figure.
A) For which values of 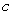 does
does 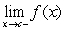 exist?
B) For which values of
exist?
B) For which values of 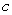 does
does 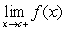 exist?
C) For which values of
exist?
C) For which values of 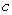 does
does 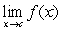 exist?
exist? 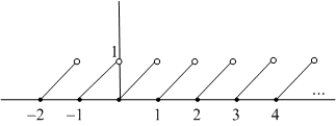
(Essay)
4.9/5  (29)
(29)
The position of a particle is given by 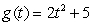 . Compute the average velocity over the time interval
. Compute the average velocity over the time interval 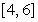 . Estimate the instantaneous velocity at
. Estimate the instantaneous velocity at 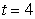 .
.
(Essay)
4.7/5  (35)
(35)
Let 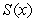 denote the slope of the line segment connecting the origin to the point
denote the slope of the line segment connecting the origin to the point 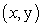 on the graph of the equation
on the graph of the equation 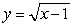 . Calculate the average rate of change of
. Calculate the average rate of change of 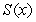 for
for 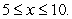
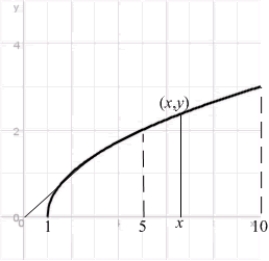
(Essay)
4.7/5  (34)
(34)
The following function is a counterexample for the converse of the Intermediate Value Theorem, which states:
If 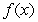 assumes all the values between
assumes all the values between 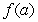 and
and 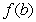 in the interval
in the interval 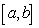 , then
, then 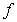 is continuous on
is continuous on 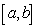 :
:
(Multiple Choice)
4.8/5  (27)
(27)
Determine whether the following statement is correct. If yes, prove it; otherwise give a counterexample
If 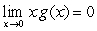 , then
, then  exists.
exists.
(True/False)
4.8/5  (39)
(39)
Determine the one-sided limits at 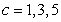 of the function
of the function  shown in the figure and state whether the limit exists at these points.
shown in the figure and state whether the limit exists at these points. 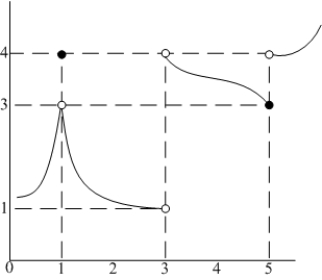
(Essay)
4.8/5  (32)
(32)
Consider the equation 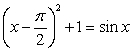 for
for 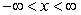 .
A) Verify that
.
A) Verify that 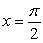 is a solution.
B) Show that
is a solution.
B) Show that 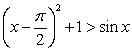 for
for 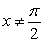 . Hint: Check the minimum value of the function on the left-hand side.
C) How many solutions does the equation have?
. Hint: Check the minimum value of the function on the left-hand side.
C) How many solutions does the equation have?
(Essay)
4.7/5  (42)
(42)
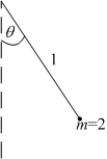
The potential energy 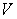 of a pendulum of length 1 and mass 2, relative to its rest position is
of a pendulum of length 1 and mass 2, relative to its rest position is 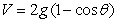 .
Compute the average rate of change of the potential energy over the angle interval
.
Compute the average rate of change of the potential energy over the angle interval 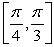 .
. 
(Essay)
4.9/5  (33)
(33)
Showing 1 - 20 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)