Deck 18: Fundamental Theorems of Vector Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/91
Play
Full screen (f)
Deck 18: Fundamental Theorems of Vector Analysis
1
Calculate the circulation of the vector field 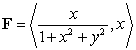 around the circle
around the circle 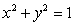 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
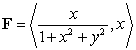 around the circle
around the circle 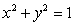 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.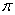
2
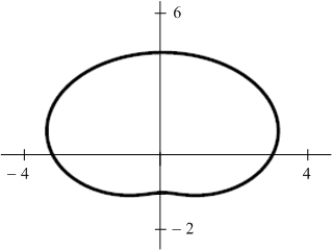
Use Green's Theorem to evaluate 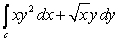 where
where 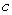 is the closed curve shown in the following figure.
is the closed curve shown in the following figure. 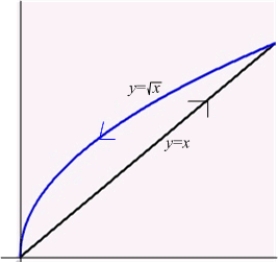
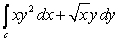 where
where 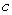 is the closed curve shown in the following figure.
is the closed curve shown in the following figure. 
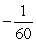
3
Evaluate the line integral 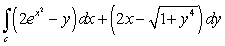 where
where 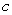 is the circle
is the circle 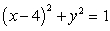 oriented in the positive direction.
oriented in the positive direction.
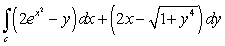 where
where  is the circle
is the circle 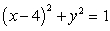 oriented in the positive direction.
oriented in the positive direction.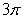
4
Compute 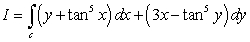 where c is the curve
where c is the curve 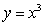 starting at the origin and ending at
starting at the origin and ending at 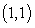 .
.
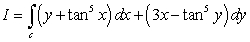 where c is the curve
where c is the curve 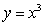 starting at the origin and ending at
starting at the origin and ending at 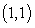 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate 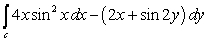 where c is the closed curve
where c is the closed curve 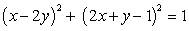 traversed in a counterclockwise direction.
traversed in a counterclockwise direction.
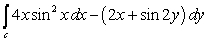 where c is the closed curve
where c is the closed curve 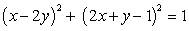 traversed in a counterclockwise direction.
traversed in a counterclockwise direction.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
6
Let 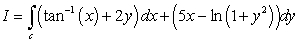 where c is the ellipse
where c is the ellipse 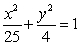 oriented in the positive direction. The value of
oriented in the positive direction. The value of 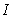 is which of the following?
is which of the following?
A)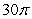
B)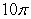
C) 0
D)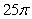
E) The integral cannot be evaluated analytically.
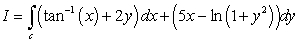 where c is the ellipse
where c is the ellipse 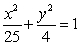 oriented in the positive direction. The value of
oriented in the positive direction. The value of 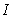 is which of the following?
is which of the following?A)
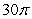
B)
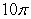
C) 0
D)
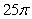
E) The integral cannot be evaluated analytically.

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate 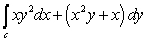 where c is the closed curve
where c is the closed curve 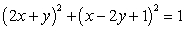 traversed in a counterclockwise direction.
traversed in a counterclockwise direction.
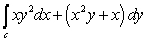 where c is the closed curve
where c is the closed curve 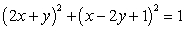 traversed in a counterclockwise direction.
traversed in a counterclockwise direction.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
8
Compute 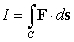 where C is the polar curve
where C is the polar curve 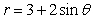 in the positive direction and
in the positive direction and 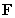 is the vector field
is the vector field 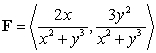 .
. 
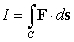 where C is the polar curve
where C is the polar curve 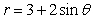 in the positive direction and
in the positive direction and 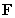 is the vector field
is the vector field 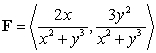 .
. 

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate 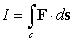 where c is the circle
where c is the circle 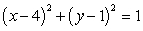 oriented counterclockwise and
oriented counterclockwise and 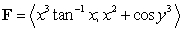 .
.
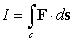 where c is the circle
where c is the circle 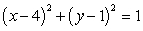 oriented counterclockwise and
oriented counterclockwise and 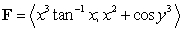 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
10
Compute 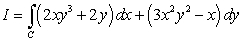 where C is the curve consisting of the line segment
where C is the curve consisting of the line segment 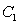 :
: 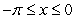 on the x-axis together with the curve
on the x-axis together with the curve 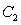 :
: 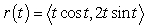
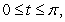 in the positive direction.
in the positive direction. 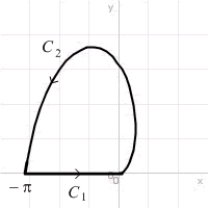
 where C is the curve consisting of the line segment
where C is the curve consisting of the line segment 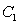 :
: 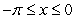 on the x-axis together with the curve
on the x-axis together with the curve 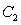 :
: 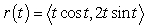
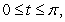 in the positive direction.
in the positive direction. 

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
11
Use Green's Theorem to calculate the counterclockwise circulation of the vector field 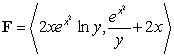 around the boundary of the region that is bounded above by the curve
around the boundary of the region that is bounded above by the curve 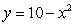 and below by the curve
and below by the curve 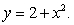
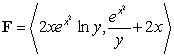 around the boundary of the region that is bounded above by the curve
around the boundary of the region that is bounded above by the curve 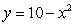 and below by the curve
and below by the curve 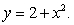

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
12
Use Green's Theorem to evaluate the line integral 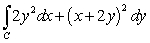 along the contour of the triangle ABD with vertices
along the contour of the triangle ABD with vertices 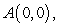
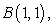
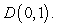
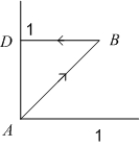
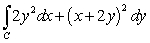 along the contour of the triangle ABD with vertices
along the contour of the triangle ABD with vertices 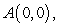
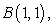
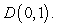


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
13
Compute the area of the shaded region whose boundary consists of the line segment 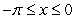 on the x axis and the curve
on the x axis and the curve 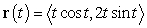 ,
,  .
. 
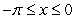 on the x axis and the curve
on the x axis and the curve 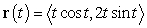 ,
, 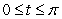 .
. 

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
14
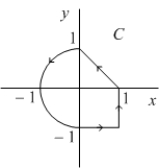
Compute 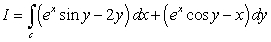 where c is the curve shown in the figure.
where c is the curve shown in the figure. 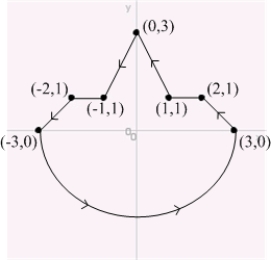
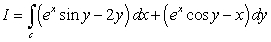 where c is the curve shown in the figure.
where c is the curve shown in the figure. 

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
15
Compute 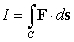 where C is the path shown in the following figure and
where C is the path shown in the following figure and 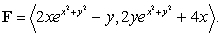
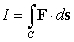 where C is the path shown in the following figure and
where C is the path shown in the following figure and 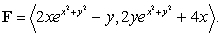


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
16
Compute the area of the region bounded by the astroid 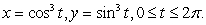
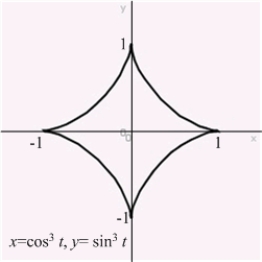
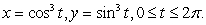


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
17
Use Green's Theorem to evaluate 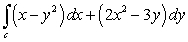 where c is the piecewise linear path starting at (0,- 2) and then traveling to (2,4), (- 2,2), and (0,- 2), in that order.
where c is the piecewise linear path starting at (0,- 2) and then traveling to (2,4), (- 2,2), and (0,- 2), in that order.
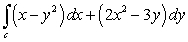 where c is the piecewise linear path starting at (0,- 2) and then traveling to (2,4), (- 2,2), and (0,- 2), in that order.
where c is the piecewise linear path starting at (0,- 2) and then traveling to (2,4), (- 2,2), and (0,- 2), in that order.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
18
Find the circulation of the field 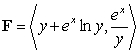 around the boundary of the region that is bounded above by the curve
around the boundary of the region that is bounded above by the curve 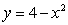 and below by
and below by 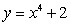 .
. 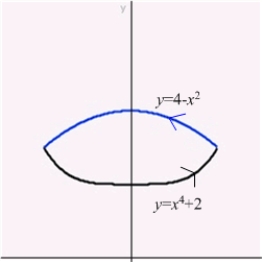
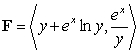 around the boundary of the region that is bounded above by the curve
around the boundary of the region that is bounded above by the curve 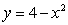 and below by
and below by 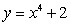 .
. 

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
19
Calculate the circulation of the vector field 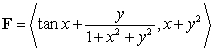 around the circle
around the circle 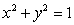 oriented counterclockwise.
oriented counterclockwise.
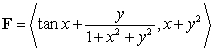 around the circle
around the circle 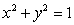 oriented counterclockwise.
oriented counterclockwise.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
20
Let 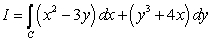 where C is the ellipse
where C is the ellipse 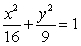 oriented counterclockwise. The value of I is which of the following?
oriented counterclockwise. The value of I is which of the following?
A) 0
B)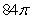
C)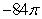
D)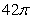
E)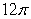
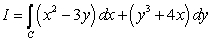 where C is the ellipse
where C is the ellipse 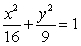 oriented counterclockwise. The value of I is which of the following?
oriented counterclockwise. The value of I is which of the following?A) 0
B)
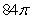
C)
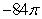
D)
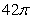
E)
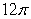

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
21
Let S be the part of the paraboloid 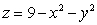 which is above the
which is above the 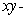 plane oriented upwards, and let
plane oriented upwards, and let 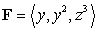 .
.
A) Explain why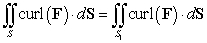 where
where 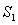 is the disc of radius 3 in the xy-plane oriented upward.
is the disc of radius 3 in the xy-plane oriented upward.
B) Compute the surface integral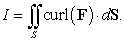
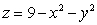 which is above the
which is above the 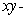 plane oriented upwards, and let
plane oriented upwards, and let 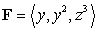 .
. A) Explain why
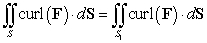 where
where 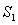 is the disc of radius 3 in the xy-plane oriented upward.
is the disc of radius 3 in the xy-plane oriented upward. B) Compute the surface integral
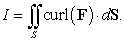

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
22
Compute 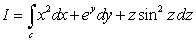 where
where 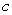 is the curve of intersection of the sphere
is the curve of intersection of the sphere 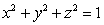 and the plane
and the plane 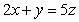 .
.
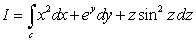 where
where 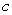 is the curve of intersection of the sphere
is the curve of intersection of the sphere 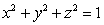 and the plane
and the plane 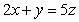 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
23
Let 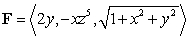 and S be the part of the sphere
and S be the part of the sphere 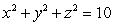 between the planes
between the planes 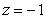 and
and 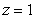 , oriented outward. The integral
, oriented outward. The integral 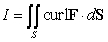 is equal to which of the following?
is equal to which of the following?
A)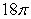
B)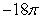
C)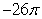
D)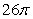
E)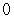
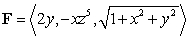 and S be the part of the sphere
and S be the part of the sphere 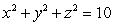 between the planes
between the planes 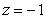 and
and 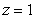 , oriented outward. The integral
, oriented outward. The integral 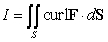 is equal to which of the following?
is equal to which of the following?A)
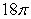
B)
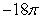
C)
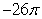
D)
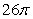
E)
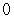

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
24
Use Stokes' Theorem to compute 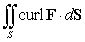 , where
, where 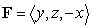 and S is the part of the surface
and S is the part of the surface 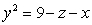 satisfying
satisfying 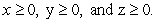 S is oriented with outward-pointing normals.
S is oriented with outward-pointing normals.
 , where
, where 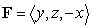 and S is the part of the surface
and S is the part of the surface 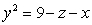 satisfying
satisfying 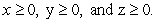 S is oriented with outward-pointing normals.
S is oriented with outward-pointing normals.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
25
Compute 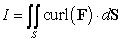 where
where 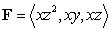 and
and 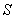 is the part of the cylinder
is the part of the cylinder 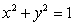 which is inside the sphere
which is inside the sphere 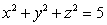 , oriented with outward-pointing normal.
, oriented with outward-pointing normal.
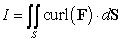 where
where 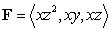 and
and 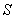 is the part of the cylinder
is the part of the cylinder 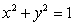 which is inside the sphere
which is inside the sphere 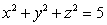 , oriented with outward-pointing normal.
, oriented with outward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
26
Use Stokes' Theorem to evaluate 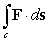 where
where 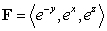 and c is the boundary of the part of the plane
and c is the boundary of the part of the plane 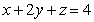 over the region
over the region 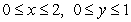 , oriented counterclockwise.
, oriented counterclockwise. 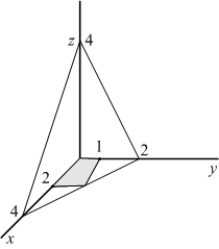
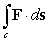 where
where 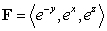 and c is the boundary of the part of the plane
and c is the boundary of the part of the plane 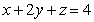 over the region
over the region 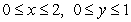 , oriented counterclockwise.
, oriented counterclockwise. 

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
27
Compute the area of the region bounded by the curve 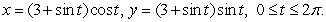
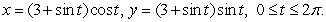

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate 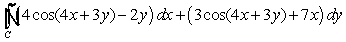 where
where 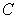 is the curve
is the curve 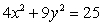 , oriented clockwise.
, oriented clockwise.
 where
where 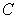 is the curve
is the curve 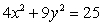 , oriented clockwise.
, oriented clockwise.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
29
Compute 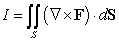 where
where 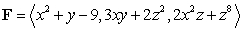 and S is the upper half of the sphere of radius 3, that is,
and S is the upper half of the sphere of radius 3, that is, 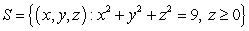 with upward-pointing normal.
with upward-pointing normal.
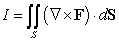 where
where 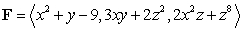 and S is the upper half of the sphere of radius 3, that is,
and S is the upper half of the sphere of radius 3, that is, 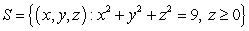 with upward-pointing normal.
with upward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate 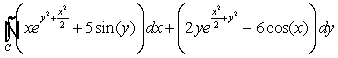 where
where 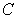 is the boundary of the unit square
is the boundary of the unit square 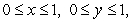 oriented clockwise.
oriented clockwise.
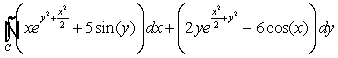 where
where 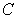 is the boundary of the unit square
is the boundary of the unit square 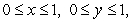 oriented clockwise.
oriented clockwise.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
31
Compute 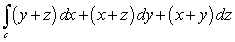 where c is the curve of intersection between the sphere
where c is the curve of intersection between the sphere 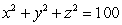 and the plane
and the plane 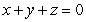 .
.
The integration on c is counterclockwise when viewing from the point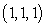 .
.
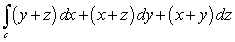 where c is the curve of intersection between the sphere
where c is the curve of intersection between the sphere 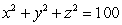 and the plane
and the plane 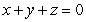 .
.The integration on c is counterclockwise when viewing from the point
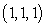 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate 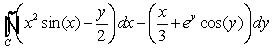 where
where 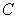 is the parallelogram with vertices
is the parallelogram with vertices 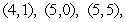 and
and 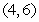 , oriented counterclockwise.
, oriented counterclockwise.
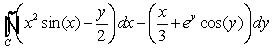 where
where 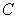 is the parallelogram with vertices
is the parallelogram with vertices 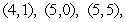 and
and 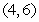 , oriented counterclockwise.
, oriented counterclockwise.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate 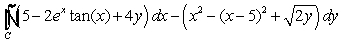 where
where 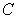 is the circle
is the circle 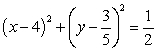 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
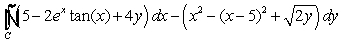 where
where 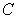 is the circle
is the circle 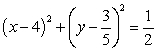 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate 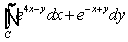 where
where 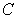 is the triangle with vertices
is the triangle with vertices 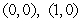 and
and 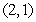 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
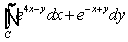 where
where 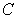 is the triangle with vertices
is the triangle with vertices 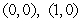 and
and 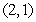 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
35
Compute 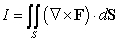 where
where 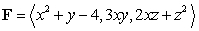 and S is the upper half of the sphere of radius 2; that is,
and S is the upper half of the sphere of radius 2; that is, 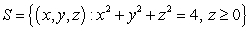 with upward-pointing normal.
with upward-pointing normal.
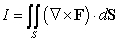 where
where 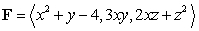 and S is the upper half of the sphere of radius 2; that is,
and S is the upper half of the sphere of radius 2; that is, 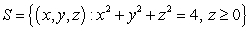 with upward-pointing normal.
with upward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate 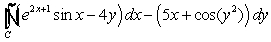 where
where 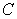 is the triangle with vertices
is the triangle with vertices 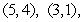 and
and 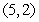 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
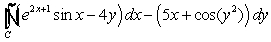 where
where 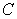 is the triangle with vertices
is the triangle with vertices 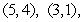 and
and 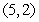 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
37
Use Green's Theorem to evaluate the integral of 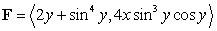 along the quarter circle
along the quarter circle 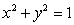 in the positive direction.
in the positive direction.
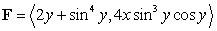 along the quarter circle
along the quarter circle 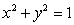 in the positive direction.
in the positive direction.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
38
Let 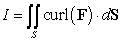 where
where 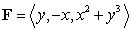 and
and 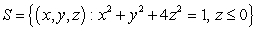 , oriented upward.
, oriented upward.
I is equal to which of the following?
A)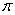
B)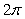
C)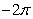
D) 0
E) None of the above.
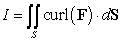 where
where 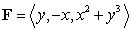 and
and 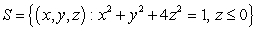 , oriented upward.
, oriented upward.I is equal to which of the following?
A)
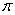
B)
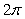
C)
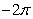
D) 0
E) None of the above.

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
39
Compute 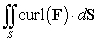 where
where 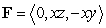 and S is the surface defined by
and S is the surface defined by 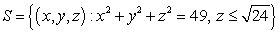 ,
,
oriented with outward pointing normal.
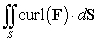 where
where 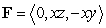 and S is the surface defined by
and S is the surface defined by 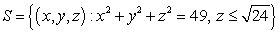 ,
,oriented with outward pointing normal.

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
40
Compute 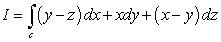 where c is the curve of intersection of the surfaces
where c is the curve of intersection of the surfaces 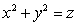 and
and 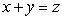 , oriented counterclockwise.
, oriented counterclockwise.
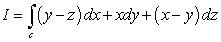 where c is the curve of intersection of the surfaces
where c is the curve of intersection of the surfaces 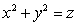 and
and 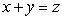 , oriented counterclockwise.
, oriented counterclockwise.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
41
Use Stokes' Theorem to compute the line integral of 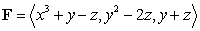 counterclockwise (as viewed from above) around the triangle with vertices
counterclockwise (as viewed from above) around the triangle with vertices 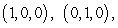 and
and 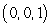 .
.
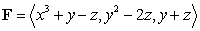 counterclockwise (as viewed from above) around the triangle with vertices
counterclockwise (as viewed from above) around the triangle with vertices 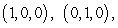 and
and 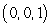 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
42
Compute 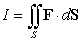 where S is the ellipsoid
where S is the ellipsoid 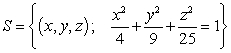 with outward-pointing normal and
with outward-pointing normal and 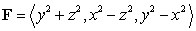 .
.
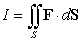 where S is the ellipsoid
where S is the ellipsoid 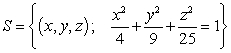 with outward-pointing normal and
with outward-pointing normal and 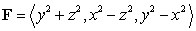 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
43
Compute 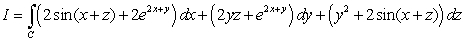 where
where 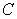 is the intersection line of the surfaces
is the intersection line of the surfaces 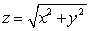 and
and 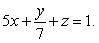
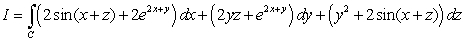 where
where  is the intersection line of the surfaces
is the intersection line of the surfaces 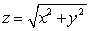 and
and 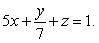

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
44
Let 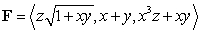 , and let S be the surface
, and let S be the surface 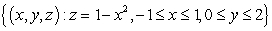 , together with the two vertical sides.
, together with the two vertical sides.
Compute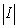 where
where 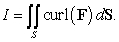
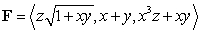 , and let S be the surface
, and let S be the surface 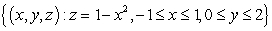 , together with the two vertical sides.
, together with the two vertical sides.Compute
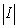 where
where 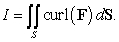

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
45
Let 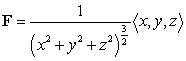 and S be a closed and smooth surface enclosing a region V.
and S be a closed and smooth surface enclosing a region V.
If V and its boundary do not include the origin, what is the value of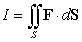 ?
?
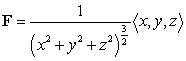 and S be a closed and smooth surface enclosing a region V.
and S be a closed and smooth surface enclosing a region V.If V and its boundary do not include the origin, what is the value of
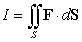 ?
?
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
46
Compute 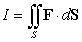 where
where 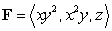 and S is the surface
and S is the surface 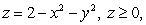 with outward pointing normal.
with outward pointing normal.
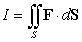 where
where 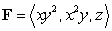 and S is the surface
and S is the surface 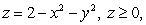 with outward pointing normal.
with outward pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
47
Compute 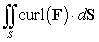 where S is the portion of the surface of the sphere with radius
where S is the portion of the surface of the sphere with radius 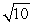 and center
and center 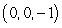 that is above the
that is above the 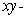 plane oriented upward, and F is the vector field
plane oriented upward, and F is the vector field 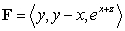 .
.
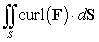 where S is the portion of the surface of the sphere with radius
where S is the portion of the surface of the sphere with radius 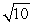 and center
and center 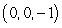 that is above the
that is above the 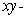 plane oriented upward, and F is the vector field
plane oriented upward, and F is the vector field 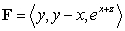 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
48
Let S be the boundary of the region V defined by 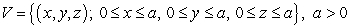 oriented with outward-pointing normal.
oriented with outward-pointing normal.
Let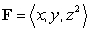 .
.
The surface integral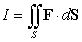 is equal to which of the following?
is equal to which of the following?
A)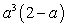
B)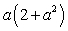
C)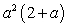
D)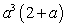
E) None of the above
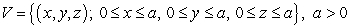 oriented with outward-pointing normal.
oriented with outward-pointing normal.Let
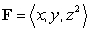 .
.The surface integral
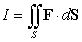 is equal to which of the following?
is equal to which of the following?A)
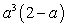
B)
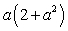
C)
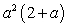
D)
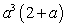
E) None of the above

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
49
Let S be the upper half of the hemisphere 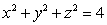 including the bottom
including the bottom 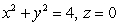 .
.
S is oriented with outward-pointing normal, and F is the vector field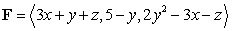 Compute
Compute 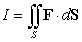 .
.
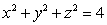 including the bottom
including the bottom 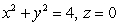 .
.S is oriented with outward-pointing normal, and F is the vector field
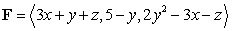 Compute
Compute 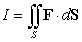 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
50
Use Stokes' Theorem to find the line integral 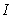 of the vector field
of the vector field 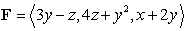 around the curve which is the intersection of the plane
around the curve which is the intersection of the plane 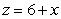 with the cylinder
with the cylinder 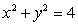 , oriented counterclockwise as viewed from above.
, oriented counterclockwise as viewed from above.
A) 0
B)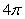
C)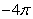
D)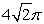
E)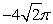
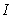 of the vector field
of the vector field 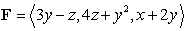 around the curve which is the intersection of the plane
around the curve which is the intersection of the plane 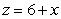 with the cylinder
with the cylinder 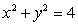 , oriented counterclockwise as viewed from above.
, oriented counterclockwise as viewed from above.A) 0
B)
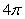
C)
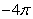
D)
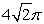
E)
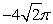

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
51
Let 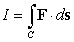 where C is the circle of intersection between the sphere
where C is the circle of intersection between the sphere 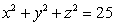 and the plane
and the plane 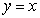 , and
, and 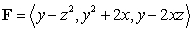 .
.
The value of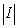 is which of the following?
is which of the following?
A)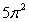
B)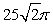
C) 0
D)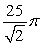
E)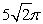
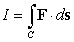 where C is the circle of intersection between the sphere
where C is the circle of intersection between the sphere 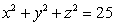 and the plane
and the plane 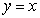 , and
, and 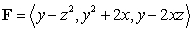 .
.The value of
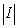 is which of the following?
is which of the following?A)
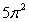
B)
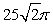
C) 0
D)
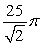
E)
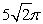

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
52
Use Stokes' Theorem to compute the line integral 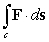 where
where 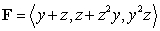 and c is the path made up of the sequence of three line segments:
and c is the path made up of the sequence of three line segments:
0 to A, A to B, and B to C. (See the figure.)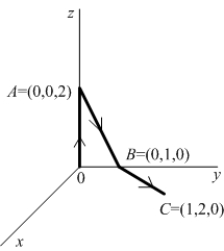
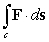 where
where 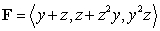 and c is the path made up of the sequence of three line segments:
and c is the path made up of the sequence of three line segments:0 to A, A to B, and B to C. (See the figure.)


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
53
Use Stokes' Theorem to compute 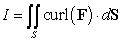 where S is the part of the surface
where S is the part of the surface 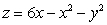 ,
, 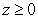 oriented outward, and
oriented outward, and 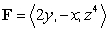 .
.
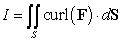 where S is the part of the surface
where S is the part of the surface 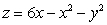 ,
, 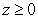 oriented outward, and
oriented outward, and 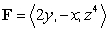 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
54
Let 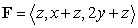 and c be the closed curve defined by the parametric equations
and c be the closed curve defined by the parametric equations 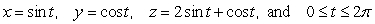 .
.
Compute the line integral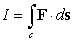 in two ways (with c oriented in the positive direction):
in two ways (with c oriented in the positive direction):
a) direct computation
b) using Stokes' Theorem
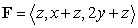 and c be the closed curve defined by the parametric equations
and c be the closed curve defined by the parametric equations 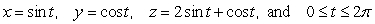 .
.Compute the line integral
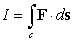 in two ways (with c oriented in the positive direction):
in two ways (with c oriented in the positive direction):a) direct computation
b) using Stokes' Theorem

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
55
Let 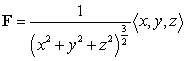 and B be a sphere of radius R centered at the origin.
and B be a sphere of radius R centered at the origin.
Referring to the integral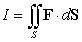 , which of the following statements is correct?
, which of the following statements is correct?
A)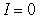 since
since 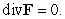
B)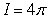 by the Divergence Theorem.
by the Divergence Theorem.
C) The Divergence Theorem cannot be applied and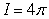 by direct computation.
by direct computation.
D) The integral is not defined since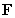 is not defined at the origin.
is not defined at the origin.
E)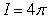 and
and 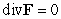 violate the Divergence Theorem.
violate the Divergence Theorem.
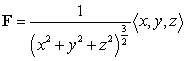 and B be a sphere of radius R centered at the origin.
and B be a sphere of radius R centered at the origin.Referring to the integral
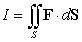 , which of the following statements is correct?
, which of the following statements is correct?A)
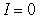 since
since 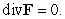
B)
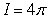 by the Divergence Theorem.
by the Divergence Theorem.C) The Divergence Theorem cannot be applied and
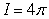 by direct computation.
by direct computation.D) The integral is not defined since
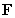 is not defined at the origin.
is not defined at the origin.E)
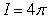 and
and 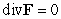 violate the Divergence Theorem.
violate the Divergence Theorem.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
56
Use Stokes' Theorem to evaluate the line integral 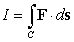 where C is the boundary of the portion of the paraboloid
where C is the boundary of the portion of the paraboloid 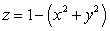
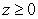 and
and 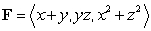 .
.
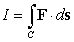 where C is the boundary of the portion of the paraboloid
where C is the boundary of the portion of the paraboloid 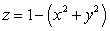
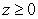 and
and 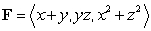 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
57
Let S be a closed and smooth surface with outward-pointing normal which is the boundary of a solid V in 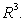 Let
Let 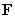 be a vector field whose components have continuous partial derivatives.
be a vector field whose components have continuous partial derivatives.
A) Compute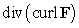 .
.
B) What is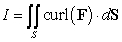 ? Explain.
? Explain.
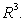 Let
Let 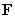 be a vector field whose components have continuous partial derivatives.
be a vector field whose components have continuous partial derivatives. A) Compute
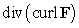 .
. B) What is
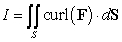 ? Explain.
? Explain.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
58
Compute 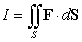 where
where 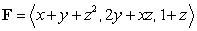 and S is the closed boundary of the cylinder
and S is the closed boundary of the cylinder 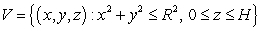 , with outward-pointing normal.
, with outward-pointing normal.
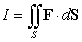 where
where 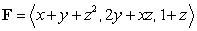 and S is the closed boundary of the cylinder
and S is the closed boundary of the cylinder 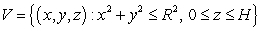 , with outward-pointing normal.
, with outward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
59
Use Stokes' Theorem to compute the flux of 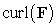 through the surface S which is the part of the paraboloid
through the surface S which is the part of the paraboloid 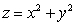 below the plane
below the plane 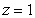 , oriented upward.
, oriented upward.
The vector field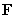 is given by
is given by 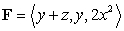 .
.
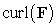 through the surface S which is the part of the paraboloid
through the surface S which is the part of the paraboloid 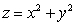 below the plane
below the plane 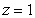 , oriented upward.
, oriented upward.The vector field
 is given by
is given by 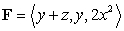 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
60
Compute 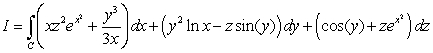 where
where 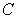 is the intersection line of the surfaces
is the intersection line of the surfaces 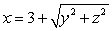 and
and 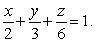
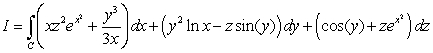 where
where 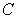 is the intersection line of the surfaces
is the intersection line of the surfaces 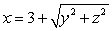 and
and 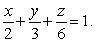

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
61
Use the Divergence Theorem to compute the surface integral 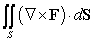 where
where 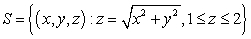 and
and 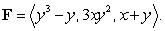 Assume
Assume 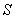 is oriented so that the normal vector points away from the z-axis.
is oriented so that the normal vector points away from the z-axis.
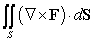 where
where 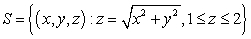 and
and 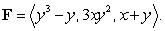 Assume
Assume 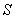 is oriented so that the normal vector points away from the z-axis.
is oriented so that the normal vector points away from the z-axis.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
62
Let 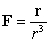 where
where 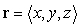 and
and 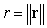 . Compute
. Compute 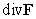 for
for 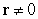 .
.
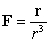 where
where 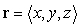 and
and 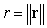 . Compute
. Compute 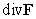 for
for 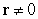 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
63
Compute the surface integral 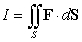 where S is the half sphere
where S is the half sphere 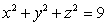 ,
, 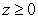 , oriented with outward pointing normal, and
, oriented with outward pointing normal, and 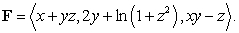
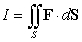 where S is the half sphere
where S is the half sphere 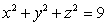 ,
, 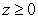 , oriented with outward pointing normal, and
, oriented with outward pointing normal, and 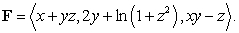

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate 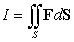 where
where 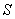 is the ellipsoid
is the ellipsoid 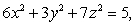 oriented outward, and
oriented outward, and 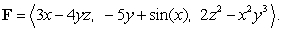
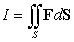 where
where 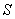 is the ellipsoid
is the ellipsoid 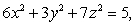 oriented outward, and
oriented outward, and 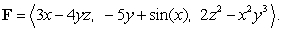

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
65
Let 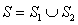 where
where 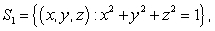
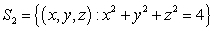 ,
, 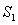 is oriented with normal pointing to the origin, and
is oriented with normal pointing to the origin, and 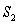 is oriented in the opposite direction.
is oriented in the opposite direction.
Let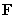 be the vector field
be the vector field 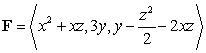 . Compute
. Compute 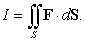
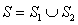 where
where 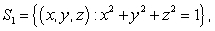
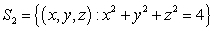 ,
, 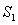 is oriented with normal pointing to the origin, and
is oriented with normal pointing to the origin, and 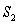 is oriented in the opposite direction.
is oriented in the opposite direction.Let
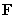 be the vector field
be the vector field 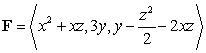 . Compute
. Compute 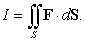

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate 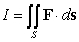 where
where 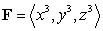 and S is the sphere
and S is the sphere 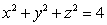 oriented with outward-pointing normal.
oriented with outward-pointing normal.
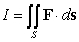 where
where 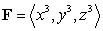 and S is the sphere
and S is the sphere 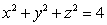 oriented with outward-pointing normal.
oriented with outward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
67
Let 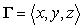 ,
, 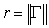 and w be a region in
and w be a region in 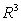 whose boundary is a closed piecewise smooth surface S. The integral
whose boundary is a closed piecewise smooth surface S. The integral 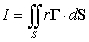 is equal to which of the following?
is equal to which of the following?
A)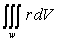
B)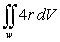
C)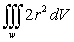
D)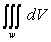
E)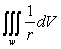
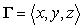 ,
, 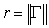 and w be a region in
and w be a region in 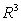 whose boundary is a closed piecewise smooth surface S. The integral
whose boundary is a closed piecewise smooth surface S. The integral 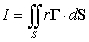 is equal to which of the following?
is equal to which of the following?A)
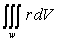
B)
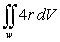
C)
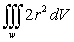
D)
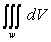
E)
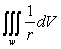

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
68
Use the Divergence Theorem to calculate the surface integral 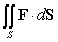 where S is the sphere
where S is the sphere 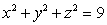 , oriented with outward-pointing normal and F is the vector field
, oriented with outward-pointing normal and F is the vector field 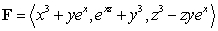 .
.
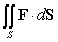 where S is the sphere
where S is the sphere 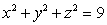 , oriented with outward-pointing normal and F is the vector field
, oriented with outward-pointing normal and F is the vector field 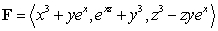 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
69
Use the Divergence Theorem to compute the surface integral 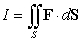 , where S is the surface
, where S is the surface 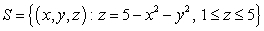 , oriented outward, and F is the vector field
, oriented outward, and F is the vector field 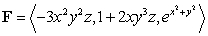 .
.
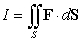 , where S is the surface
, where S is the surface 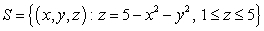 , oriented outward, and F is the vector field
, oriented outward, and F is the vector field 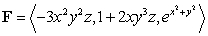 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
70
Compute 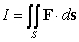 where
where 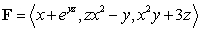 and
and 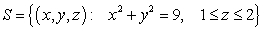 , oriented outward.
, oriented outward.
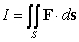 where
where 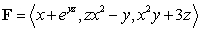 and
and 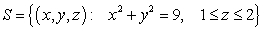 , oriented outward.
, oriented outward.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
71
Compute 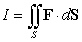 where
where 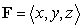 and S is the boundary of the pyramid determined by the planes
and S is the boundary of the pyramid determined by the planes 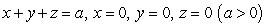 .
.
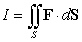 where
where 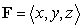 and S is the boundary of the pyramid determined by the planes
and S is the boundary of the pyramid determined by the planes 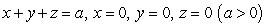 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate 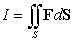 where
where 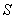 is the boundary of the region enclosed by the surfaces
is the boundary of the region enclosed by the surfaces 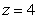 and
and 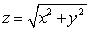 and
and 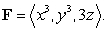
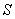 is oriented with outward-pointing normal.
is oriented with outward-pointing normal.
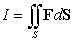 where
where 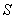 is the boundary of the region enclosed by the surfaces
is the boundary of the region enclosed by the surfaces 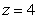 and
and 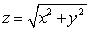 and
and 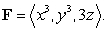
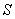 is oriented with outward-pointing normal.
is oriented with outward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate 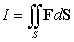 where
where 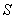 is the ellipsoid
is the ellipsoid 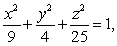 oriented outward, and
oriented outward, and 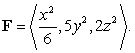
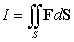 where
where 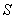 is the ellipsoid
is the ellipsoid 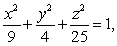 oriented outward, and
oriented outward, and 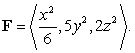

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
74
Let 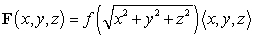 . Write the condition for f so that for all
. Write the condition for f so that for all 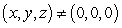 ,
, 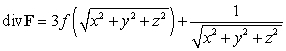 .
.
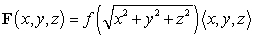 . Write the condition for f so that for all
. Write the condition for f so that for all 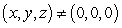 ,
, 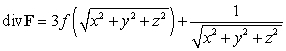 .
.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
75
Let 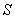 be the surface area of the box in the figure with dimensions
be the surface area of the box in the figure with dimensions 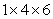 , and let W be the interior of the box.
, and let W be the interior of the box. 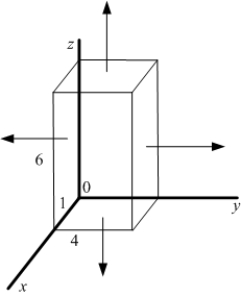 Let F be the vector field
Let F be the vector field 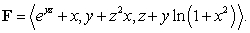 Which of the following integrals are equal?
Which of the following integrals are equal?
A)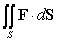
B)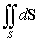
C)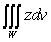
D)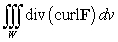
E)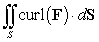
 be the surface area of the box in the figure with dimensions
be the surface area of the box in the figure with dimensions 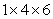 , and let W be the interior of the box.
, and let W be the interior of the box.  Let F be the vector field
Let F be the vector field 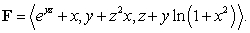 Which of the following integrals are equal?
Which of the following integrals are equal? A)
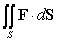
B)
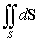
C)
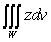
D)
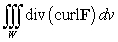
E)
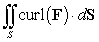

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
76
Let  . Compute the surface integral
. Compute the surface integral 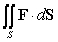 where S is the surface
where S is the surface 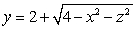 oriented so that the normal points toward increasing y.
oriented so that the normal points toward increasing y.
 . Compute the surface integral
. Compute the surface integral 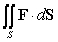 where S is the surface
where S is the surface 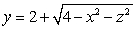 oriented so that the normal points toward increasing y.
oriented so that the normal points toward increasing y.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
77
Compute 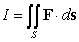 where
where 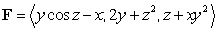 and
and 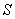 is the part of the paraboloid
is the part of the paraboloid 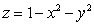 above the plane
above the plane 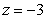 , oriented outward.
, oriented outward.
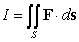 where
where 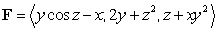 and
and 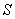 is the part of the paraboloid
is the part of the paraboloid 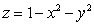 above the plane
above the plane 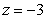 , oriented outward.
, oriented outward.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
78
Let 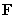 be the vector field
be the vector field 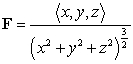 , w be a region in
, w be a region in 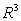 containing the origin in its interior , and S be the boundary of w that is a closed surface with outward-pointing normal.
containing the origin in its interior , and S be the boundary of w that is a closed surface with outward-pointing normal.
Compute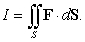
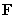 be the vector field
be the vector field 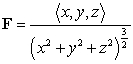 , w be a region in
, w be a region in 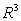 containing the origin in its interior , and S be the boundary of w that is a closed surface with outward-pointing normal.
containing the origin in its interior , and S be the boundary of w that is a closed surface with outward-pointing normal.Compute

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate 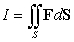 where
where 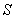 is the boundary of the region enclosed by the surfaces
is the boundary of the region enclosed by the surfaces 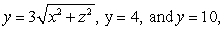 and
and 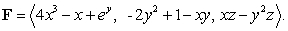
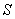 is oriented with inward-pointing normal.
is oriented with inward-pointing normal.
 where
where 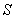 is the boundary of the region enclosed by the surfaces
is the boundary of the region enclosed by the surfaces 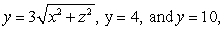 and
and 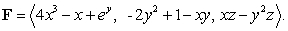
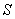 is oriented with inward-pointing normal.
is oriented with inward-pointing normal.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
80
Use the Divergence Theorem to evaluate 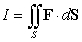 where
where 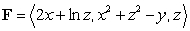 and S is the surface
and S is the surface 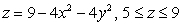 , oriented outward.
, oriented outward.
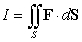 where
where 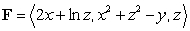 and S is the surface
and S is the surface 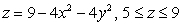 , oriented outward.
, oriented outward.
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck


