Exam 18: Fundamental Theorems of Vector Analysis
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Let 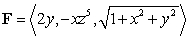 and S be the part of the sphere
and S be the part of the sphere 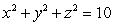 between the planes
between the planes 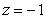 and
and 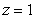 , oriented outward. The integral
, oriented outward. The integral 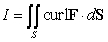 is equal to which of the following?
is equal to which of the following?
Free
(Multiple Choice)
4.9/5  (28)
(28)
Correct Answer:
A
Compute 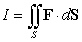 where
where 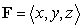 and S is the boundary of the pyramid determined by the planes
and S is the boundary of the pyramid determined by the planes 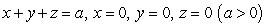 .
.
Free
(Essay)
4.8/5  (39)
(39)
Correct Answer:
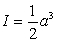
Use Stokes' Theorem to compute 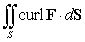 , where
, where 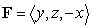 and S is the part of the surface
and S is the part of the surface 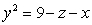 satisfying
satisfying 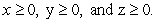 S is oriented with outward-pointing normals.
S is oriented with outward-pointing normals.
Free
(Short Answer)
4.7/5  (27)
(27)
Correct Answer:
4.5
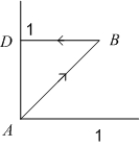
Use Green's Theorem to evaluate the line integral 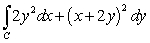 along the contour of the triangle ABD with vertices
along the contour of the triangle ABD with vertices 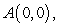
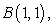
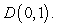
(Essay)
4.8/5  (30)
(30)
Compute 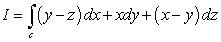 where c is the curve of intersection of the surfaces
where c is the curve of intersection of the surfaces 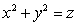 and
and 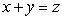 , oriented counterclockwise.
, oriented counterclockwise.
(Essay)
4.9/5  (44)
(44)
Use Green's Theorem to evaluate 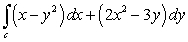 where c is the piecewise linear path starting at (0,- 2) and then traveling to (2,4), (- 2,2), and (0,- 2), in that order.
where c is the piecewise linear path starting at (0,- 2) and then traveling to (2,4), (- 2,2), and (0,- 2), in that order.
(Essay)
4.7/5  (39)
(39)
Evaluate 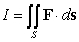 where
where 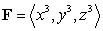 and S is the sphere
and S is the sphere 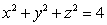 oriented with outward-pointing normal.
oriented with outward-pointing normal.
(Essay)
4.8/5  (30)
(30)
Let S be the part of the paraboloid 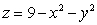 which is above the
which is above the 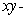 plane oriented upwards, and let
plane oriented upwards, and let 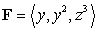 .
A) Explain why
.
A) Explain why 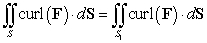 where
where 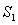 is the disc of radius 3 in the xy-plane oriented upward.
B) Compute the surface integral
is the disc of radius 3 in the xy-plane oriented upward.
B) Compute the surface integral 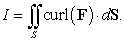
(Essay)
4.8/5  (26)
(26)
Compute 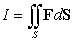 where
where 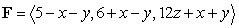 and
and 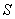 is the boundary of the tetrahedron with vertices
is the boundary of the tetrahedron with vertices 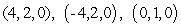 and
and 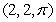 , oriented with outward-pointing normal.
, oriented with outward-pointing normal.
(Essay)
4.8/5  (36)
(36)
Compute 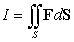 where
where 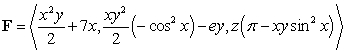 and
and 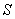 is the boundary of the tetrahedron with vertices
is the boundary of the tetrahedron with vertices 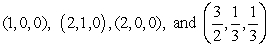 , oriented with outward-pointing normal.
, oriented with outward-pointing normal.
(Essay)
4.7/5  (36)
(36)
Use Green's Theorem to evaluate 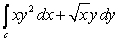 where
where 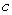 is the closed curve shown in the following figure.
is the closed curve shown in the following figure. 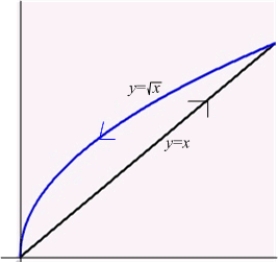
(Essay)
4.9/5  (38)
(38)
Let 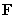 be the vector field
be the vector field 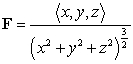 , w be a region in
, w be a region in 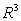 containing the origin in its interior , and S be the boundary of w that is a closed surface with outward-pointing normal.
Compute
containing the origin in its interior , and S be the boundary of w that is a closed surface with outward-pointing normal.
Compute 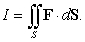
(Essay)
4.8/5  (37)
(37)
Let 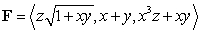 , and let S be the surface
, and let S be the surface 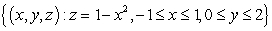 , together with the two vertical sides.
Compute
, together with the two vertical sides.
Compute 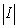 where
where 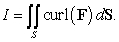
(Essay)
4.8/5  (38)
(38)
Let S be the boundary of the region V defined by 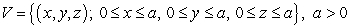 oriented with outward-pointing normal.
Let
oriented with outward-pointing normal.
Let 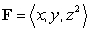 .
The surface integral
.
The surface integral 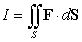 is equal to which of the following?
is equal to which of the following?
(Multiple Choice)
4.9/5  (31)
(31)
Showing 1 - 20 of 91
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)