Deck 16: Multiple Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/98
Play
Full screen (f)
Deck 16: Multiple Integration
1
Find the volume of the solid which lies under the surface 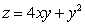 and above the rectangle
and above the rectangle 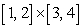 .
.
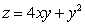 and above the rectangle
and above the rectangle 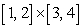 .
.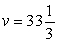
2
The value of the integral 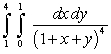 is which of the following?
is which of the following?
A)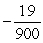
B)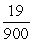
C)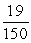
D)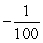
E) None of the above.
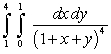 is which of the following?
is which of the following?A)
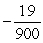
B)
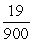
C)
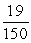
D)
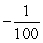
E) None of the above.
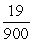
3
Evaluate 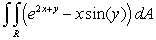 , where
, where 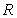 is the rectangle
is the rectangle 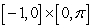 .
.
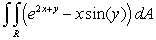 , where
, where 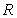 is the rectangle
is the rectangle 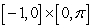 .
.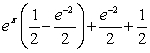
4
Compute the integral 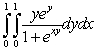 .
.
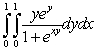 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
5
Find the volume of the region under the surface 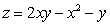 and above the rectangle
and above the rectangle 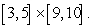
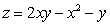 and above the rectangle
and above the rectangle 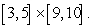

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the integral 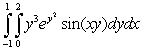 .
.
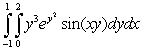 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the double integral of the function 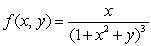 over the rectangle
over the rectangle 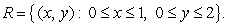
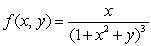 over the rectangle
over the rectangle 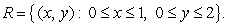

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the iterated integral 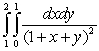 .
.
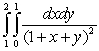 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
9
Let 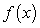 be the following function:
be the following function: 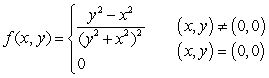 .
.
a) Compute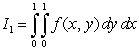 and
and 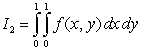 .
.
b) Is Fubini's Theorem valid in this case? If not, explain why.
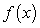 be the following function:
be the following function: 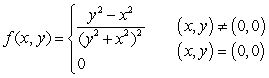 .
.a) Compute
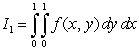 and
and 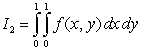 .
.b) Is Fubini's Theorem valid in this case? If not, explain why.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate 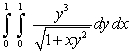 .
.
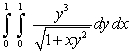 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
11
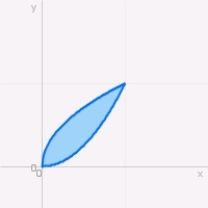
Sketch the region of integration and compute 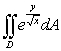 ,
,
where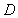 is the region enclosed by the parabolas
is the region enclosed by the parabolas 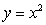 and
and 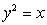 .
. 
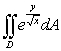 ,
,where
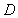 is the region enclosed by the parabolas
is the region enclosed by the parabolas 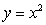 and
and 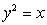 .
. 

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the double integral of the function over the rectangle.
A)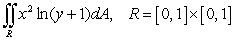
B)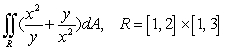
A)
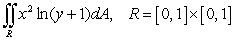
B)
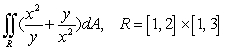

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
13
Compute 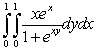 .
.
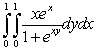 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
14
Let 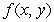 be continuous. If the equality
be continuous. If the equality 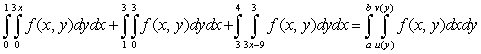 holds, then:
holds, then:
A)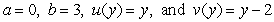 .
.
B)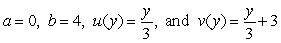 .
.
C)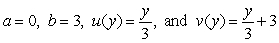 .
.
D)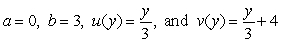 .
.
E) There are no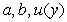 , and
, and 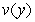 that satisfy the equality.
that satisfy the equality.
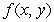 be continuous. If the equality
be continuous. If the equality 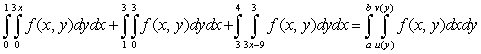 holds, then:
holds, then:A)
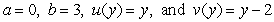 .
.B)
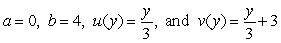 .
.C)
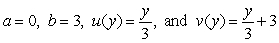 .
.D)
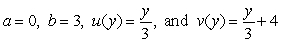 .
.E) There are no
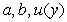 , and
, and 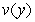 that satisfy the equality.
that satisfy the equality.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
15
Compute 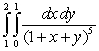 .
.
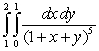 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate 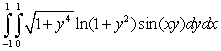 .
.
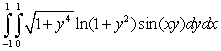 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
17
Find the volume of the solid bounded by the surface 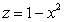 and the planes
and the planes 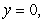
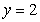 , and
, and 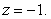
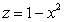 and the planes
and the planes 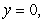
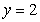 , and
, and 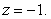

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
18
Compute 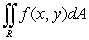 , where
, where 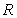 is the parallelogram with edges
is the parallelogram with edges 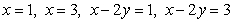 , and
, and 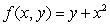 .
.
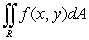 , where
, where 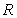 is the parallelogram with edges
is the parallelogram with edges 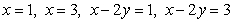 , and
, and 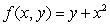 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
19
Find the volume of the region under the surface 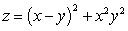 and above the rectangle
and above the rectangle 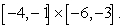
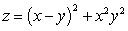 and above the rectangle
and above the rectangle 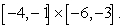

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
20
The value of the integral 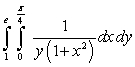 is which of the following?
is which of the following?
A)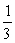
B)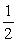
C)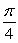
D) 1
E) None of the above.
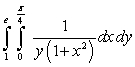 is which of the following?
is which of the following?A)
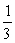
B)
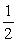
C)
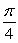
D) 1
E) None of the above.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate 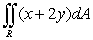 , where
, where 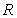 is the triangle with vertices
is the triangle with vertices 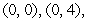 and
and 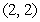 .
.
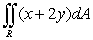 , where
, where 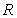 is the triangle with vertices
is the triangle with vertices 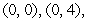 and
and 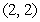 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
22
Let 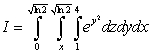 .
.
A) Rewrite the integral in the order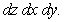
B) Compute the integral in the preferable order.
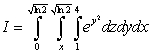 .
. A) Rewrite the integral in the order
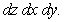
B) Compute the integral in the preferable order.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
23
The volume of the tetrahedron bounded by the coordinate planes and the plane through 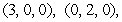 and
and 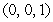 is which of the following?
is which of the following?
A)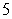
B)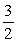
C)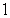
D)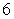
E)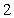
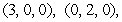 and
and 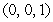 is which of the following?
is which of the following?A)
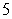
B)
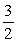
C)
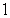
D)
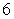
E)
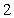

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate 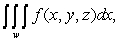 where
where 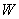 is the region enclosed by the planes
is the region enclosed by the planes 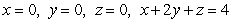 , and
, and 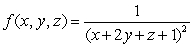 .
.
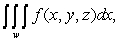 where
where 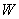 is the region enclosed by the planes
is the region enclosed by the planes 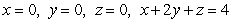 , and
, and 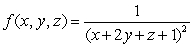 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
25
A lamina bounded by the curves 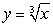 ,
, 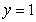 , and
, and 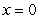 has mass density
has mass density 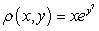 . Find the mass of the lamina.
. Find the mass of the lamina.
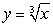 ,
, 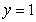 , and
, and 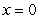 has mass density
has mass density 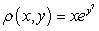 . Find the mass of the lamina.
. Find the mass of the lamina.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
26
The value of the integral 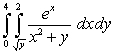 is which of the following?
is which of the following?
A)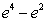
B)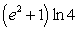
C)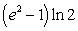
D)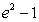
E) The integral cannot be evaluated analytically.
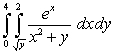 is which of the following?
is which of the following?A)
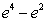
B)
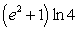
C)
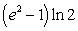
D)
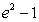
E) The integral cannot be evaluated analytically.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the 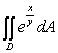 , where
, where 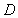 is the region
is the region 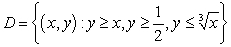 .
.
Sketch the region of integration.
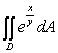 , where
, where 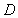 is the region
is the region 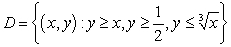 .
.Sketch the region of integration.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
28
The volume of the tetrahedron with the vertices 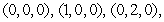 and
and 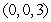 is which of the following?
is which of the following?
A)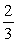
B)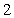
C)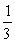
D)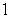
E) None of the above.
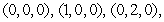 and
and 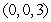 is which of the following?
is which of the following?A)
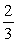
B)
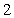
C)
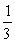
D)
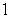
E) None of the above.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
29
Given the integral 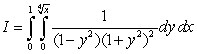 :
:
a) sketch the region of integration and reverse the order of integration.
b) evaluate the integral.
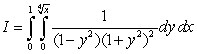 :
:a) sketch the region of integration and reverse the order of integration.
b) evaluate the integral.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
30
Compute the 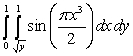 .
.
Sketch the region of integration.
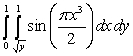 .
.Sketch the region of integration.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
31
Let 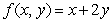 and
and 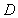 be the triangle in the
be the triangle in the 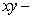 plane enclosed by the lines
plane enclosed by the lines 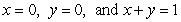 .
.
Find the set of all the points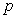 in
in 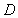 such that
such that 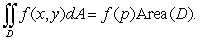
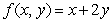 and
and 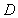 be the triangle in the
be the triangle in the 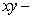 plane enclosed by the lines
plane enclosed by the lines 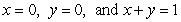 .
.Find the set of all the points
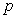 in
in 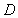 such that
such that 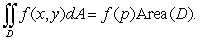

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
32
a) Change the order of integration in the integral 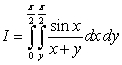 .
.
b) Evaluate the integral.
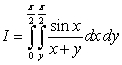 .
.b) Evaluate the integral.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
33
Let 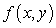 be the following function on the rectangle
be the following function on the rectangle 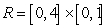 :
: 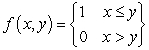 .
.
A) ?
A) Compute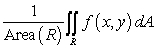
B) Can you find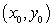 in
in 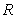 such that
such that 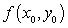 is equal to the value in
is equal to the value in
C) Explain why there is no contradiction with the Mean Value Theorem.
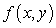 be the following function on the rectangle
be the following function on the rectangle 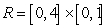 :
: 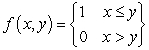 .
. A) ?
A) Compute
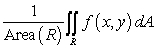
B) Can you find
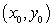 in
in 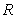 such that
such that 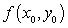 is equal to the value in
is equal to the value in C) Explain why there is no contradiction with the Mean Value Theorem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the integral 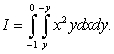
A) Draw the region of integration and reverse the order of integration.
B) Compute the integral in any order you choose.
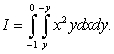
A) Draw the region of integration and reverse the order of integration.
B) Compute the integral in any order you choose.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
35
Rewrite the following integral in the order 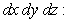
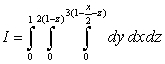 .
.
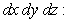
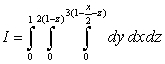 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the triple integral 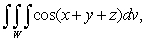 where
where 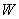 is the solid tetrahedron with vertices
is the solid tetrahedron with vertices 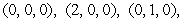 and
and 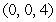 .
.
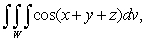 where
where 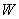 is the solid tetrahedron with vertices
is the solid tetrahedron with vertices 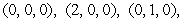 and
and 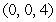 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the integral 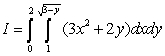 .
.
A) Sketch the region of integration
B) Interchange the order of integration.
C) Evaluate the integral.
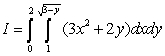 .
. A) Sketch the region of integration
B) Interchange the order of integration.
C) Evaluate the integral.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
38
Let 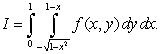 a) Sketch the region of integration and reverse the order of integration.
a) Sketch the region of integration and reverse the order of integration.
b) Compute the integral for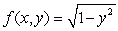 .
.
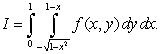 a) Sketch the region of integration and reverse the order of integration.
a) Sketch the region of integration and reverse the order of integration.b) Compute the integral for
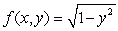 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
39
a) Change the order of integration in the integral 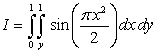 .
.
b) Evaluate the integral.
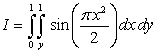 .
.b) Evaluate the integral.


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
40
The volume of the ellipsoid 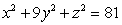 is which of the following?
is which of the following?
A)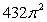
B)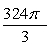
C)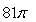
D)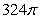
E)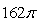
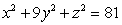 is which of the following?
is which of the following?A)
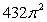
B)
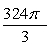
C)
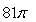
D)
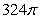
E)
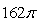

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
41
Integrate 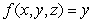 over the region in the first octant above
over the region in the first octant above 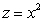 and below
and below 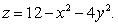
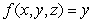 over the region in the first octant above
over the region in the first octant above 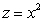 and below
and below 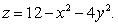

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
42
Compute the volume of the region enclosed by the plane 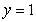 and the paraboloid
and the paraboloid 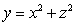 .
.
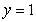 and the paraboloid
and the paraboloid 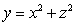 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
43
Compute the volume of the region satisfying 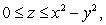
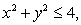 and
and 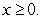
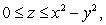
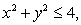 and
and 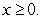

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
44
Let 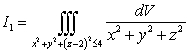 ,
, 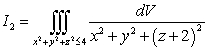 , and
, and 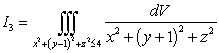 Which of the following statements holds?
Which of the following statements holds?
A)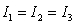 .
.
B)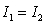 but
but 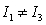 .
.
C)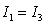 but
but 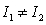 .
.
D)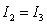 but
but 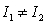 .
.
E) The three integrals are different.
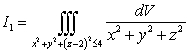 ,
, 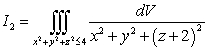 , and
, and 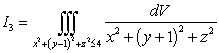 Which of the following statements holds?
Which of the following statements holds?A)
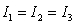 .
.B)
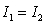 but
but 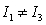 .
.C)
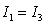 but
but 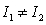 .
.D)
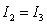 but
but 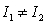 .
.E) The three integrals are different.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
45
Use cylindrical coordinates to compute the volume 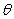 of the solid enclosed by the surfaces
of the solid enclosed by the surfaces 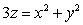 and
and 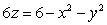 .
.
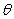 of the solid enclosed by the surfaces
of the solid enclosed by the surfaces 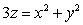 and
and 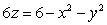 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
46
Use polar coordinates to compute 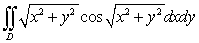 , where
, where 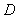 is the region in the first quadrant enclosed by the circles
is the region in the first quadrant enclosed by the circles 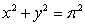 and
and 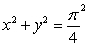 .
.
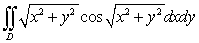 , where
, where 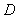 is the region in the first quadrant enclosed by the circles
is the region in the first quadrant enclosed by the circles 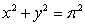 and
and 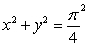 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
47
Let 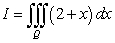 where
where 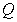 is the tetrahedron with vertices at
is the tetrahedron with vertices at 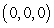 ,
, 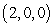 ,
, 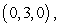 and
and 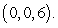 Write
Write 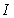 as an iterated integral in the orders
as an iterated integral in the orders 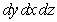 and
and 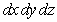 .
.
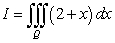 where
where 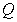 is the tetrahedron with vertices at
is the tetrahedron with vertices at 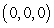 ,
, 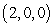 ,
, 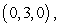 and
and 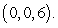 Write
Write 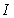 as an iterated integral in the orders
as an iterated integral in the orders 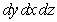 and
and 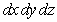 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
48
Use cylindrical coordinates to compute the volume of the solid bounded by the paraboloid 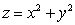 and the upper sphere
and the upper sphere 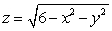 .
.
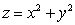 and the upper sphere
and the upper sphere 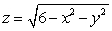 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
49
Find the volume of the ellipsoid 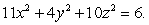
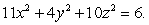

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
50
The average value of 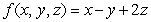 over the tetrahedron with vertices
over the tetrahedron with vertices 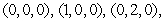 and
and 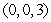 is which of the following?
is which of the following?
A)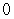
B)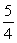
C)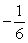
D)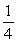
E)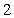
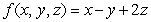 over the tetrahedron with vertices
over the tetrahedron with vertices 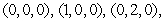 and
and 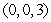 is which of the following?
is which of the following?A)
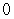
B)
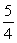
C)
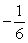
D)
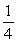
E)
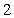

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate 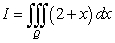 where
where 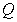 is the tetrahedron with vertices at
is the tetrahedron with vertices at 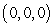 ,
, 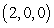 ,
, 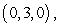 and
and 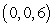 in the order
in the order 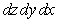 .
.
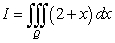 where
where 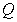 is the tetrahedron with vertices at
is the tetrahedron with vertices at 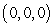 ,
, 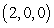 ,
, 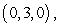 and
and 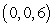 in the order
in the order 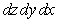 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
52
Rewrite the integral 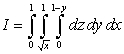 in the order
in the order 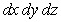 .
.
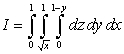 in the order
in the order 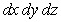 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
53
Convert the following integral to cylindrical and spherical coordinates: 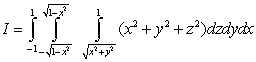 .
.
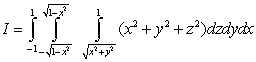 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
54
The value of 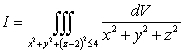 is which of the following?
is which of the following?
A)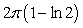
B)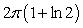
C)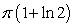
D)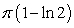
E) None of these answers are correct.
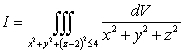 is which of the following?
is which of the following?A)
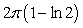
B)
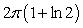
C)
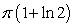
D)
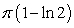
E) None of these answers are correct.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
55
Rewrite the integral 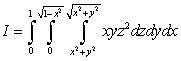 using cylindrical coordinates and evaluate the integral.
using cylindrical coordinates and evaluate the integral.
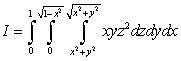 using cylindrical coordinates and evaluate the integral.
using cylindrical coordinates and evaluate the integral.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
56
Let 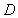 be the region
be the region 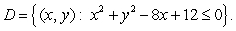 Using polar coordinates
Using polar coordinates 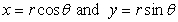 for the integral
for the integral 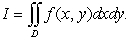
A) find the limits of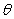 .
.
B) find the limits of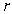 .
.
C) convert the integral to polar coordinates.
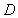 be the region
be the region 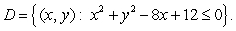 Using polar coordinates
Using polar coordinates 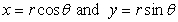 for the integral
for the integral 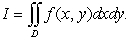
A) find the limits of
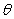 .
. B) find the limits of
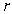 .
. C) convert the integral to polar coordinates.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
57
Find 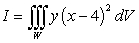 if
if 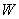 is the region satisfying
is the region satisfying 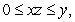
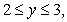 and
and 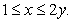
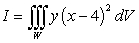 if
if 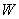 is the region satisfying
is the region satisfying 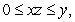
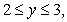 and
and 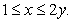

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
58
Let 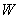 be the region in the
be the region in the 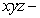 space defined by the inequalities
space defined by the inequalities 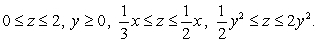
A) Rewrite the inequalities for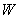 in adequate form for evaluating
in adequate form for evaluating 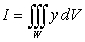 in the order
in the order 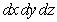 .
.
B) Evaluate the integral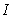 .
.
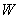 be the region in the
be the region in the 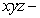 space defined by the inequalities
space defined by the inequalities 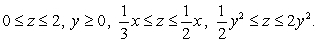
A) Rewrite the inequalities for
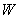 in adequate form for evaluating
in adequate form for evaluating 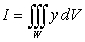 in the order
in the order 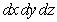 .
. B) Evaluate the integral
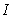 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
59
The volume of the region enclosed by the cylinder 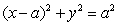 , the cone
, the cone 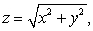 and the
and the 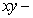 plane is which of the following?
plane is which of the following?
A)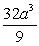
B)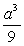
C)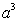
D)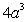
E) None of the above.
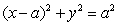 , the cone
, the cone 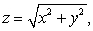 and the
and the 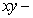 plane is which of the following?
plane is which of the following?A)
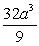
B)
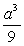
C)
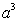
D)
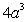
E) None of the above.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
60
Use spherical coordinates to compute 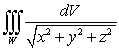 , where
, where 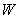 is the solid bounded by the spheres
is the solid bounded by the spheres 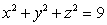 and
and 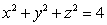 .
.
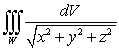 , where
, where 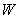 is the solid bounded by the spheres
is the solid bounded by the spheres 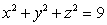 and
and 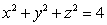 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
61
Find the coordinates of the centroid of the plate bounded by the lines 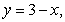
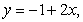 and
and 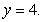
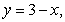
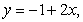 and
and 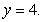

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
62
The solid in the first octant bounded by the sphere 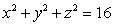 above, by the cone
above, by the cone 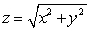 below, and by the planes
below, and by the planes 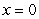 and
and 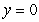 on the side, has a density
on the side, has a density 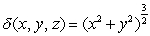 .
.
Set up the integral for the mass of the solid
A) in rectangular coordinates.
B) in cylindrical coordinates.
C) in spherical coordinates.
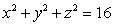 above, by the cone
above, by the cone 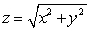 below, and by the planes
below, and by the planes 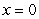 and
and 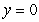 on the side, has a density
on the side, has a density 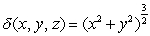 .
.Set up the integral for the mass of the solid
A) in rectangular coordinates.
B) in cylindrical coordinates.
C) in spherical coordinates.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
63
Find the coordinates of the centroid for the sector of the unit disk 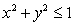 satisfying
satisfying 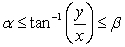 where
where 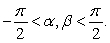
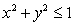 satisfying
satisfying 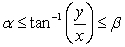 where
where 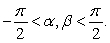

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
64
Find the volume of the portion of the ball 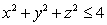 lying above the plane
lying above the plane 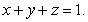
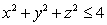 lying above the plane
lying above the plane 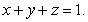

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
65
Integrate the function 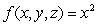 over the region bounded by
over the region bounded by 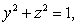
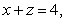 and
and 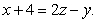
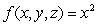 over the region bounded by
over the region bounded by 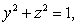
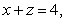 and
and 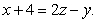

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
66
Let 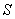 be the solid occupying the region
be the solid occupying the region 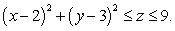 Find the moment of inertia
Find the moment of inertia 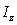 about the
about the 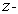 axis if
axis if 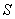 has density
has density 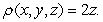
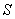 be the solid occupying the region
be the solid occupying the region 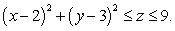 Find the moment of inertia
Find the moment of inertia 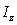 about the
about the 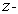 axis if
axis if 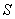 has density
has density 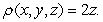

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
67
Integrate the function 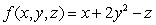 over the region bounded by the cone
over the region bounded by the cone 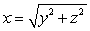 and the paraboloid
and the paraboloid 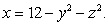
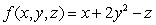 over the region bounded by the cone
over the region bounded by the cone 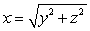 and the paraboloid
and the paraboloid 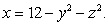

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
68
Use spherical coordinates to set up the integral to compute the volume of the solid bounded by the paraboloid 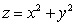 and the upper sphere
and the upper sphere 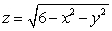 . (Do not evaluate the integral.)
. (Do not evaluate the integral.)
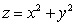 and the upper sphere
and the upper sphere 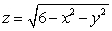 . (Do not evaluate the integral.)
. (Do not evaluate the integral.)
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
69
If the density is 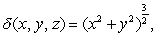 find the mass of the solid in the first octant bounded by the sphere
find the mass of the solid in the first octant bounded by the sphere 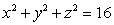 above, by the cone
above, by the cone 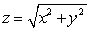 below, and by the planes
below, and by the planes 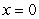 and
and 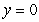 on the side.
on the side.
A)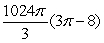
B)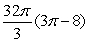
C)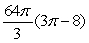
D)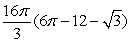
E) None of the above
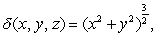 find the mass of the solid in the first octant bounded by the sphere
find the mass of the solid in the first octant bounded by the sphere 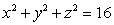 above, by the cone
above, by the cone 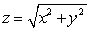 below, and by the planes
below, and by the planes 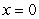 and
and 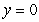 on the side.
on the side.A)
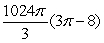
B)
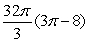
C)
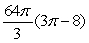
D)
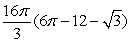
E) None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
70
If the mass density is 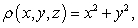 find
find 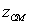 for the solid occupying the region which satisfies
for the solid occupying the region which satisfies 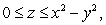
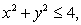 and
and 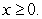
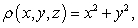 find
find 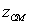 for the solid occupying the region which satisfies
for the solid occupying the region which satisfies 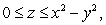
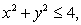 and
and 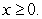

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
71
Find the mass and 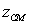 of the solid in the first octant bounded by the cylinder
of the solid in the first octant bounded by the cylinder 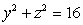 and the planes
and the planes 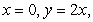 and
and 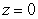 , assuming that the mass density is
, assuming that the mass density is 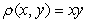 .
.
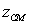 of the solid in the first octant bounded by the cylinder
of the solid in the first octant bounded by the cylinder 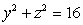 and the planes
and the planes 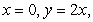 and
and 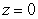 , assuming that the mass density is
, assuming that the mass density is 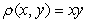 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
72
Find the coordinates of the centroid for the region described by 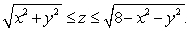

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
73
The 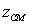 of the solid region that is inside the cylinder
of the solid region that is inside the cylinder 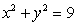 , below the paraboloid
, below the paraboloid 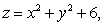 and above the
and above the 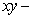 plane (assuming
plane (assuming 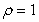 ) is which of the following?
) is which of the following?
A)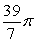
B)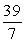
C)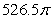
D) 6
E) None of the above
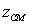 of the solid region that is inside the cylinder
of the solid region that is inside the cylinder 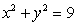 , below the paraboloid
, below the paraboloid 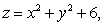 and above the
and above the 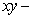 plane (assuming
plane (assuming 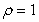 ) is which of the following?
) is which of the following?A)
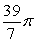
B)
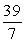
C)
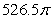
D) 6
E) None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
74
Find the volume of the region inside the cylinder 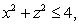
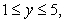 but outside the paraboloid
but outside the paraboloid 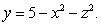
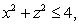
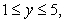 but outside the paraboloid
but outside the paraboloid 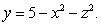

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
75
Use cylindrical coordinates to compute the volume of the solid 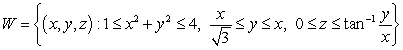 .
.
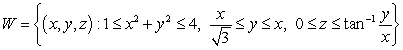 .
.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
76
Find the volume of the region satisfying 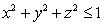 and
and 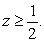
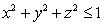 and
and 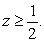

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
77
Find the volume of the portion of the ball 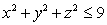 satisfying
satisfying 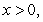
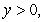 and lying above the surface defined by
and lying above the surface defined by 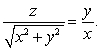
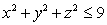 satisfying
satisfying 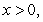
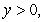 and lying above the surface defined by
and lying above the surface defined by 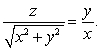

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
78
Find the center of mass of the tetrahedron 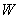 in the first octant formed by the coordinate planes and the plane
in the first octant formed by the coordinate planes and the plane 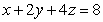 . (Assume the density is
. (Assume the density is 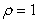 .)
.)
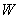 in the first octant formed by the coordinate planes and the plane
in the first octant formed by the coordinate planes and the plane 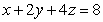 . (Assume the density is
. (Assume the density is 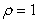 .)
.)
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
79
Consider a flat plate occupying the region in the 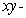 plane bounded by the curves
plane bounded by the curves 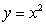 and
and 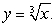 If the plate has density
If the plate has density 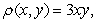 find the moment of inertia
find the moment of inertia 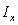 about the
about the 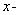 axis.
axis.
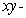 plane bounded by the curves
plane bounded by the curves 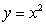 and
and 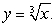 If the plate has density
If the plate has density 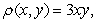 find the moment of inertia
find the moment of inertia 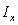 about the
about the 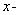 axis.
axis.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
80
Let 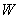 be the solid bounded by the cylinder
be the solid bounded by the cylinder 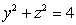 and the planes
and the planes 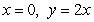 , and
, and 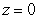 in the first octant. The density of the solid is
in the first octant. The density of the solid is 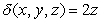 .
.
A) Find the mass of the solid.
B) Find the center of mass of the solid.
 be the solid bounded by the cylinder
be the solid bounded by the cylinder 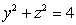 and the planes
and the planes 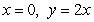 , and
, and 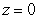 in the first octant. The density of the solid is
in the first octant. The density of the solid is 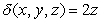 .
. A) Find the mass of the solid.
B) Find the center of mass of the solid.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck


