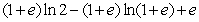Exam 16: Multiple Integration
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Use polar coordinates to compute 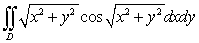 , where
, where 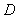 is the region in the first quadrant enclosed by the circles
is the region in the first quadrant enclosed by the circles 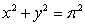 and
and 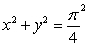 .
.
Free
(Essay)
4.9/5  (38)
(38)
Correct Answer:
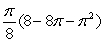
Consider the integral 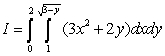 .
A) Sketch the region of integration
.
A) Sketch the region of integration 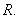 B) Interchange the order of integration.
C) Evaluate the integral.
B) Interchange the order of integration.
C) Evaluate the integral.
Free
(Essay)
4.9/5  (34)
(34)
Correct Answer:
A) 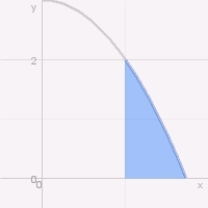 B)
B) 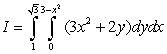 C)
C) 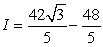
Use cylindrical coordinates to compute the volume 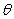 of the solid enclosed by the surfaces
of the solid enclosed by the surfaces 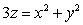 and
and 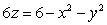 .
.
(Essay)
4.9/5  (27)
(27)
Let 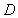 be the region
be the region 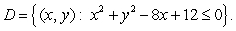 Using polar coordinates
Using polar coordinates 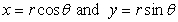 for the integral
for the integral 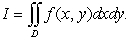 A) find the limits of
A) find the limits of 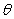 .
B) find the limits of
.
B) find the limits of 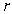 .
C) convert the integral to polar coordinates.
.
C) convert the integral to polar coordinates.
(Essay)
4.9/5  (29)
(29)
Let 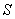 be the solid occupying the region
be the solid occupying the region 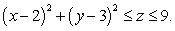 Find the moment of inertia
Find the moment of inertia 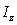 about the
about the 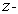 axis if
axis if 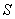 has density
has density 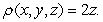
(Essay)
4.8/5  (37)
(37)
Define the function 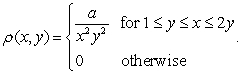 Find the value of
Find the value of 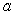 which makes
which makes 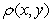 a probability density function.
a probability density function.
(Essay)
4.8/5  (26)
(26)
Let 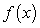 be the following function:
be the following function: 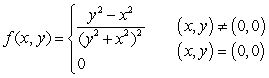 .
a) Compute
.
a) Compute 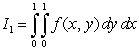 and
and 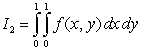 .
b) Is Fubini's Theorem valid in this case? If not, explain why.
.
b) Is Fubini's Theorem valid in this case? If not, explain why.
(Essay)
4.7/5  (34)
(34)
Let 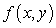 be the following function on the rectangle
be the following function on the rectangle 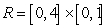 :
: 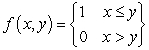 .
A) ?
A) Compute
.
A) ?
A) Compute 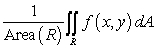 B) Can you find
B) Can you find 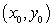 in
in 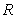 such that
such that 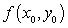 is equal to the value in
C) Explain why there is no contradiction with the Mean Value Theorem.
is equal to the value in
C) Explain why there is no contradiction with the Mean Value Theorem.
(Essay)
4.9/5  (39)
(39)
Find the volume of the solid which lies under the surface 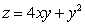 and above the rectangle
and above the rectangle 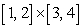 .
.
(Essay)
4.8/5  (32)
(32)
Showing 1 - 20 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)