Deck 14: Calculus of Vector-Valued Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/99
Play
Full screen (f)
Deck 14: Calculus of Vector-Valued Functions
1
Find the point of intersection of the space curves 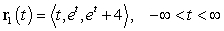 , and
, and 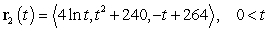 .
.
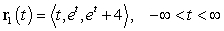 , and
, and 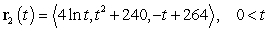 .
.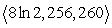
2
Find the curve traced by the following vector valued function and describe it with a Cartesian equation. 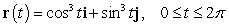
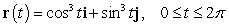
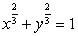
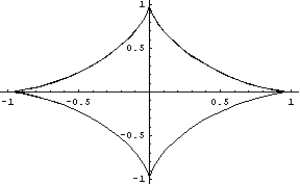
3
Let 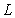 be the intersection curve between the surfaces
be the intersection curve between the surfaces 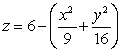 and
and 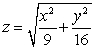 .
.
If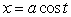 ,
, 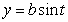 , and
, and 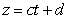 is a parameterization of
is a parameterization of 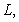 then:
then:
A)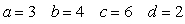
B)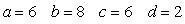
C)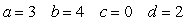
D)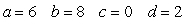
E)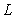 cannot be parameterized by a parameterization in this form.
cannot be parameterized by a parameterization in this form.
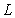 be the intersection curve between the surfaces
be the intersection curve between the surfaces 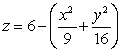 and
and 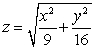 .
.If
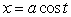 ,
, 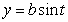 , and
, and 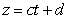 is a parameterization of
is a parameterization of 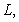 then:
then:A)
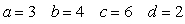
B)
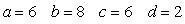
C)
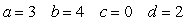
D)
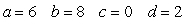
E)
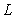 cannot be parameterized by a parameterization in this form.
cannot be parameterized by a parameterization in this form.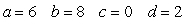
4
Particle 1 and Particle 2 are flying through space. At time 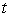 , the position of Particle 1 is given by
, the position of Particle 1 is given by 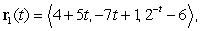 and the position of Particle 2 is given by
and the position of Particle 2 is given by 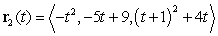 . Do the particles ever collide? If so, where?
. Do the particles ever collide? If so, where?
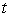 , the position of Particle 1 is given by
, the position of Particle 1 is given by 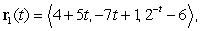 and the position of Particle 2 is given by
and the position of Particle 2 is given by 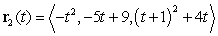 . Do the particles ever collide? If so, where?
. Do the particles ever collide? If so, where?
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
5
Parameterize the circle of radius 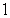 with center
with center 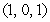 located in the plane
located in the plane 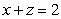 .
.
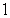 with center
with center 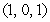 located in the plane
located in the plane 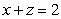 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
6
Find a parameterization for the line of intersection of the planes 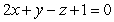 and
and 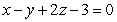 .
.
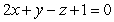 and
and 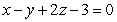 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
7
Find the point of intersection between the curve 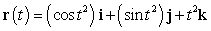 and the plane
and the plane 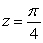 .
.
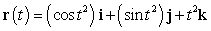 and the plane
and the plane 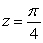 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
8
Parameterize the curve of intersection between the sphere 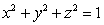 and the cone
and the cone 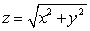 and identify the curve.
and identify the curve.
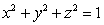 and the cone
and the cone 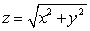 and identify the curve.
and identify the curve.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
9
Parameterize the curve of intersection of the surfaces 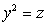 and
and 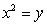 .
.
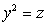 and
and 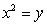 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
10
The curve 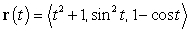 intersects the
intersects the 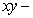 plane at which of the following points?
plane at which of the following points?
A)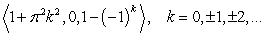
B)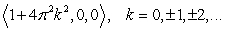
C)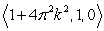
D)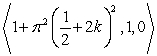
E) The curve does not intersect the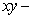 plane.
plane.
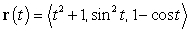 intersects the
intersects the 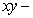 plane at which of the following points?
plane at which of the following points?A)
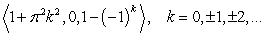
B)
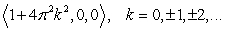
C)
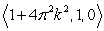
D)
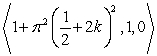
E) The curve does not intersect the
 plane.
plane.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the linear paths 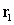 and
and 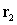 , described by
, described by 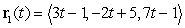 and
and 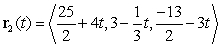 . Do the lines traced by
. Do the lines traced by 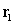 and
and 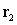 intersect? If so, where?
intersect? If so, where?
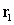 and
and 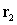 , described by
, described by 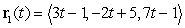 and
and 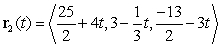 . Do the lines traced by
. Do the lines traced by 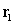 and
and 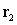 intersect? If so, where?
intersect? If so, where?
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the paths 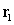 and
and 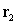 intersect.
intersect. 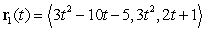
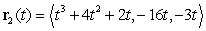
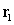 and
and 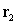 intersect.
intersect. 

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the curve traced by 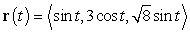 .
.
This curve lies on both a sphere and a plane.
A) Find the equation of the sphere.
B) Find the equation of the plane.
C) Explain why the curve traced by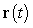 lies on a circle.
lies on a circle.
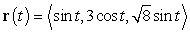 .
.This curve lies on both a sphere and a plane.
A) Find the equation of the sphere.
B) Find the equation of the plane.
C) Explain why the curve traced by
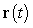 lies on a circle.
lies on a circle.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
14
The curve 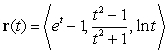 intersects the
intersects the 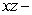 plane at which of the following points?
plane at which of the following points?
A)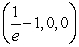
B)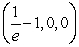 and
and 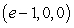
C)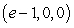
D)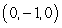
E) The curve does not intersect the - plane.
- plane.
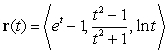 intersects the
intersects the 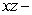 plane at which of the following points?
plane at which of the following points?A)
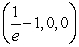
B)
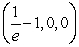 and
and 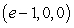
C)
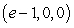
D)
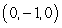
E) The curve does not intersect the
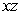 - plane.
- plane.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
15
Describe the curve traced by the following vector valued function, and sketch the graph of this curve. 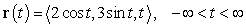
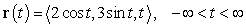

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
16
Determine the radius, center, and plane containing the circle parametrized by 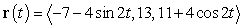 .
.
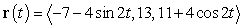 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
17
Find 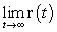 where
where 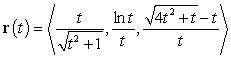 .
.
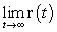 where
where 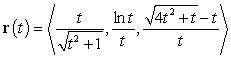 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
18
Find a parametric equation for the tangent line to the path 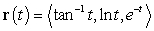 at the point where
at the point where 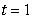 .
.
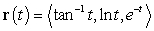 at the point where
at the point where 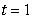 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
19
Parameterize the curve of intersection of the hemisphere 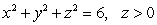 and the parabolic cylinder
and the parabolic cylinder 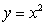 .
.
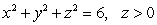 and the parabolic cylinder
and the parabolic cylinder 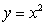 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
20
Find the domain of the vector-valued function 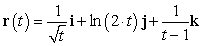 .
.
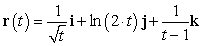 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
21
Parametrize the tangent line to the curve 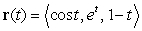 at the point where
at the point where 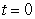 .
.
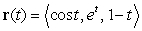 at the point where
at the point where 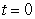 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
22
Find a point on the curve 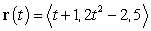 where the tangent line is parallel to the plane
where the tangent line is parallel to the plane 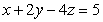 .
.
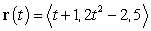 where the tangent line is parallel to the plane
where the tangent line is parallel to the plane 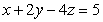 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
23
Find the arc length of the curve 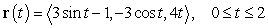 .
.
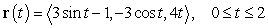 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
24
Find the tangent line to the curve 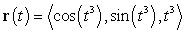 at point
at point 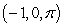 .
.
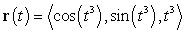 at point
at point 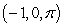 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
25
Find 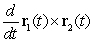 , where
, where 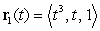 and
and 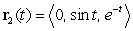 :
:
A) by first computing the cross product and then differentiating.
B) using the cross product rule.
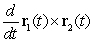 , where
, where 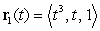 and
and 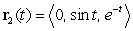 :
: A) by first computing the cross product and then differentiating.
B) using the cross product rule.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
26
Compute 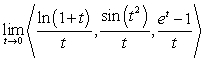 .
.
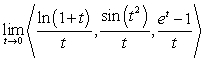 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
27
A moving object has a position vector function 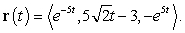
A) Find the speed of the object at time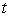 .
.
B) Find the distance traveled by the object between times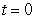 and
and 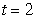 .
.
C) When does the object have minimum speed?
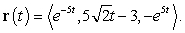
A) Find the speed of the object at time
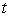 .
. B) Find the distance traveled by the object between times
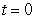 and
and 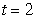 .
. C) When does the object have minimum speed?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate 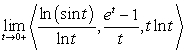 .
.
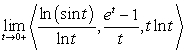 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
29
Find the points on the curve 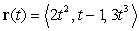 where the tangent line is parallel to the plane
where the tangent line is parallel to the plane 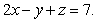
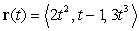 where the tangent line is parallel to the plane
where the tangent line is parallel to the plane 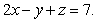

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
30
Find the length of the curve described by the vector function 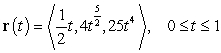 .
.
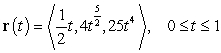 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
31
Find a vector parametrization for the tangent line to the curve 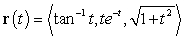 at the point
at the point 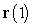 .
.
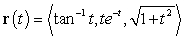 at the point
at the point 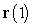 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
32
The path of a particle satisfies 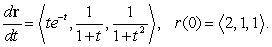 At
At 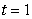 , the particle is located at:
, the particle is located at:
A)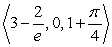 .
.
B)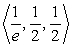 .
.
C)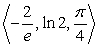 .
.
D)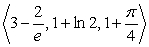 .
.
E) The data are not sufficient.
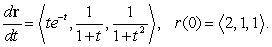 At
At 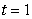 , the particle is located at:
, the particle is located at:A)
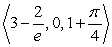 .
.B)
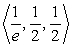 .
.C)
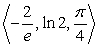 .
.D)
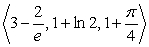 .
.E) The data are not sufficient.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
33
Find an arc length parametrization for the line 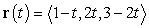 .
.
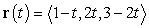 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
34
Find 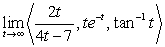 .
.
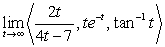 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
35
Find the arc length parametrization of the curve 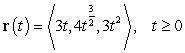 .
.
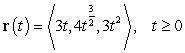 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the definite integrals.
A)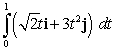
B)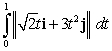
A)
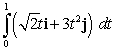
B)
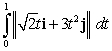

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
37
Let 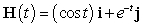 ,
, 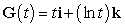 , and
, and 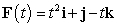 .
.
A) Compute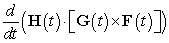 using the cross product and the dot product rules for differentiating.
using the cross product and the dot product rules for differentiating.
A).
B) Compute the scalar triple product, differentiate it, and compare with the result in
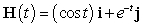 ,
, 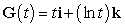 , and
, and 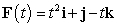 .
. A) Compute
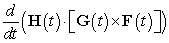 using the cross product and the dot product rules for differentiating.
using the cross product and the dot product rules for differentiating. A).
B) Compute the scalar triple product, differentiate it, and compare with the result in

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
38
Let 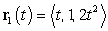 and
and 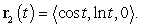
A) Compute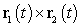 and then differentiate the resulting function.
and then differentiate the resulting function.
B) Find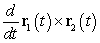 using the cross-product rule for differentiation.
using the cross-product rule for differentiation.
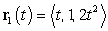 and
and 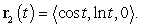
A) Compute
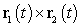 and then differentiate the resulting function.
and then differentiate the resulting function. B) Find
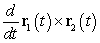 using the cross-product rule for differentiation.
using the cross-product rule for differentiation.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
39
The points on the curve 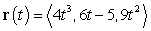 , where the tangent line is perpendicular to the plane
, where the tangent line is perpendicular to the plane 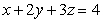 , are:
, are:
A)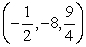 .
.
B)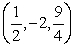 .
.
C)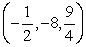 and
and 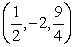 .
.
D)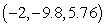 and
and 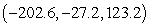 .
.
E) There are no such points.
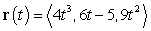 , where the tangent line is perpendicular to the plane
, where the tangent line is perpendicular to the plane 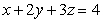 , are:
, are:A)
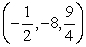 .
.B)
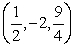 .
.C)
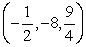 and
and 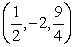 .
.D)
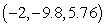 and
and 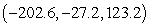 .
.E) There are no such points.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
40
Find 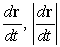 , and
, and 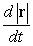 for
for 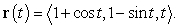
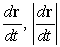 , and
, and 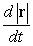 for
for 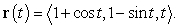

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
41
The path of a certain particle is parametrized by 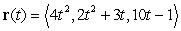 ,
, 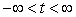 . At what time
. At what time 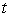 is the minimum speed of the particle achieved?
is the minimum speed of the particle achieved?
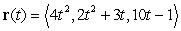 ,
, 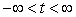 . At what time
. At what time 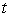 is the minimum speed of the particle achieved?
is the minimum speed of the particle achieved?
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
42
The path of a projectile is parametrized by 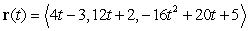 . Find the projectile's speed when it reached the point
. Find the projectile's speed when it reached the point 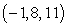 .
.
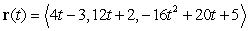 . Find the projectile's speed when it reached the point
. Find the projectile's speed when it reached the point 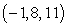 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
43
Find the arc length parametrization of the curve 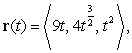
 .
.
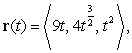
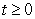 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
44
Find the speed at time 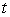 of the particle that is traveling along the curve
of the particle that is traveling along the curve 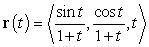 .
.
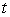 of the particle that is traveling along the curve
of the particle that is traveling along the curve 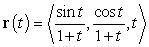 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
45
The curvature for 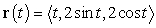 is:
is:
A)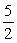 .
.
B)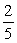 .
.
C)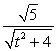 .
.
D)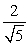 .
.
E) none of the above.
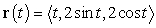 is:
is:A)
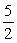 .
.B)
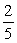 .
.C)
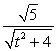 .
.D)
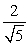 .
.E) none of the above.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
46
Find the curvature of 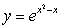 at
at 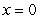 .
.
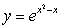 at
at 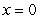 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
47
A particle moves along the curve 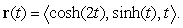 The speed of the particle at
The speed of the particle at 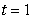 is approximately:
is approximately:
A)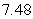 .
.
B)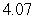 .
.
C)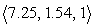 .
.
D)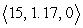 .
.
E)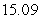 .
.
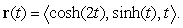 The speed of the particle at
The speed of the particle at 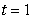 is approximately:
is approximately:A)
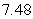 .
.B)
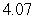 .
.C)
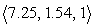 .
.D)
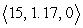 .
.E)
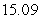 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
48
Find an arc length parametrization of the curve 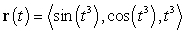 .
.
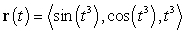 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
49
Find the unit normal vector 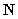 , the curvature
, the curvature 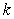 , and the center of the osculating circle at
, and the center of the osculating circle at 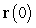 , for the curve
, for the curve 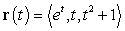 .
.
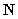 , the curvature
, the curvature 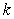 , and the center of the osculating circle at
, and the center of the osculating circle at 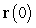 , for the curve
, for the curve 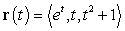 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
50
The position of a particle traversing a circular path is given by 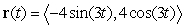 . Find the speed of the particle at time
. Find the speed of the particle at time 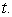
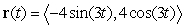 . Find the speed of the particle at time
. Find the speed of the particle at time 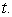

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
51
Find the length of the curve 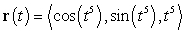 for
for 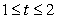 .
.
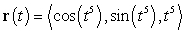 for
for 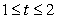 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
52
Particle 1 follows the path parametrized by 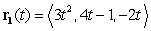 , while Particle 2 follows the path parametrized by
, while Particle 2 follows the path parametrized by 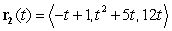 . At what time
. At what time 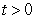 does the speed of Particle 1 match the speed of Particle 2?
does the speed of Particle 1 match the speed of Particle 2?
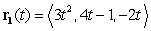 , while Particle 2 follows the path parametrized by
, while Particle 2 follows the path parametrized by 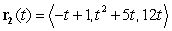 . At what time
. At what time 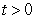 does the speed of Particle 1 match the speed of Particle 2?
does the speed of Particle 1 match the speed of Particle 2?
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
53
Find the length of the curve described by the vector function 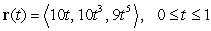 .
.
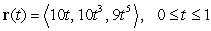 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
54
Find an arc length parametrization of the curve 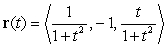 ,
,
and identify the curve.
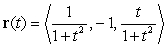 ,
,and identify the curve.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
55
Find the length of the curve 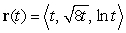 for
for 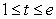 .
.
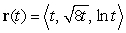 for
for 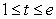 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
56
The length of the curve 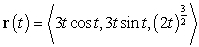 for
for  is:
is:
A)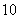 .
.
B)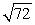 .
.
C)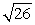 .
.
D)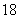 .
.
E) none of the above.
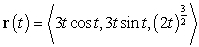 for
for  is:
is:A)
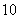 .
.B)
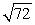 .
.C)
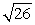 .
.D)
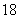 .
.E) none of the above.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
57
The position of a particle for time 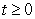 is given by
is given by 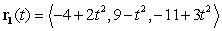 . Find the speed of the particle when it touches the curve parametrized by
. Find the speed of the particle when it touches the curve parametrized by 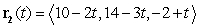 .
.
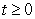 is given by
is given by 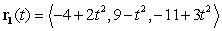 . Find the speed of the particle when it touches the curve parametrized by
. Find the speed of the particle when it touches the curve parametrized by 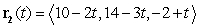 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
58
The position of a particle is given by 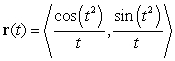 ,
, 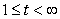 . What is the limit of the particle's speed as
. What is the limit of the particle's speed as 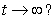
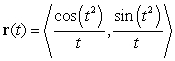 ,
, 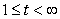 . What is the limit of the particle's speed as
. What is the limit of the particle's speed as 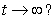

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
59
Find the arc length of the Archimedes spiral 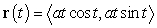 for
for 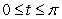 . Assume a is positive.
. Assume a is positive.
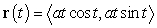 for
for 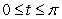 . Assume a is positive.
. Assume a is positive.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
60
The curvature of 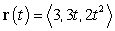 at the point
at the point 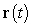 is:
is:
A)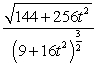 .
.
B)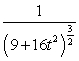 .
.
C)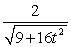 .
.
D)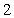 .
.
E)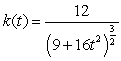 .
.
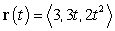 at the point
at the point 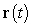 is:
is:A)
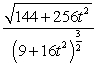 .
.B)
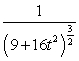 .
.C)
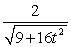 .
.D)
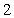 .
.E)
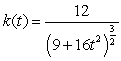 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
61
A particle moves along the curve 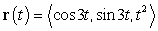 . Compute the velocity and acceleration vectors at
. Compute the velocity and acceleration vectors at 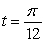 .
.
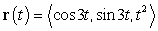 . Compute the velocity and acceleration vectors at
. Compute the velocity and acceleration vectors at 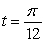 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
62
For the parametrization 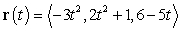 , find the curvature of the path at
, find the curvature of the path at 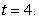
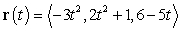 , find the curvature of the path at
, find the curvature of the path at 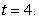

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
63
Find the unit normal vector to 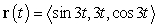 at
at 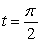 .
.
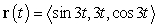 at
at 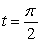 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
64
Find the curvature of the plane curve 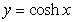 , and identify the point at which the curve has maximum curvature.
, and identify the point at which the curve has maximum curvature.
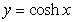 , and identify the point at which the curve has maximum curvature.
, and identify the point at which the curve has maximum curvature.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
65
Find the unit tangent of the curve 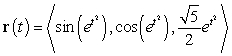 at
at 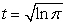 .
.
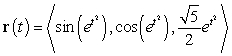 at
at 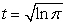 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
66
The curvature of 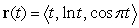 at
at 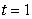 is:
is:
A)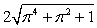 .
.
B)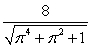 .
.
C)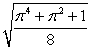 .
.
D)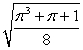 .
.
E) none of the above.
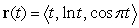 at
at 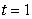 is:
is:A)
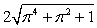 .
.B)
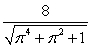 .
.C)
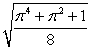 .
.D)
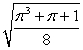 .
.E) none of the above.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
67
Find a parametrization of the osculating circle at 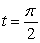 if
if 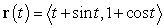 .
.
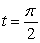 if
if 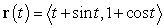 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
68
Let 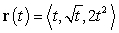 . Decompose
. Decompose 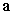 into tangential and normal components at
into tangential and normal components at 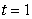 .
.
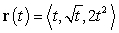 . Decompose
. Decompose 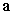 into tangential and normal components at
into tangential and normal components at 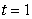 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
69
For the parametrization 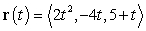 , find the unit normal vector at
, find the unit normal vector at 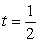 .
.
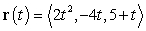 , find the unit normal vector at
, find the unit normal vector at 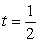 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
70
The acceleration vector of a moving particle is 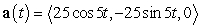 . Its initial position is
. Its initial position is 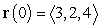 , and its initial velocity is
, and its initial velocity is 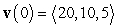 .
.
Find the vector position at time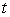 .
.
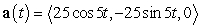 . Its initial position is
. Its initial position is 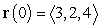 , and its initial velocity is
, and its initial velocity is 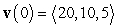 .
.Find the vector position at time
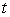 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
71
The curvature of 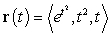 at the point where
at the point where 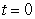 is:
is:
A)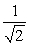 .
.
B)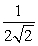 .
.
C)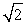 .
.
D) 1.
E)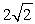 .
.
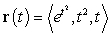 at the point where
at the point where 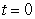 is:
is:A)
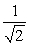 .
.B)
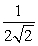 .
.C)
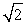 .
.D) 1.
E)
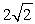 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the helix 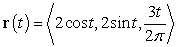 .
.
A) Find the unit tangent vector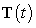 and the unit normal vector
and the unit normal vector 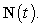
B) Find the curvature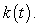
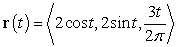 .
. A) Find the unit tangent vector
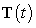 and the unit normal vector
and the unit normal vector 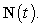
B) Find the curvature
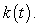

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the helix 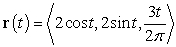 .
.
A) Compute the center and the radius of the osculating circle at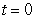 .
.
B) Compute the equation of the plane containing the osculating circle.
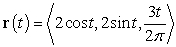 .
. A) Compute the center and the radius of the osculating circle at
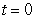 .
. B) Compute the equation of the plane containing the osculating circle.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
74
A particle moves along the curve 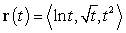 .
.
Compute the velocity and acceleration vectors at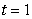 .
.
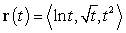 .
.Compute the velocity and acceleration vectors at
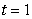 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
75
Find the center and radius of the osculating circle at 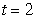 if
if 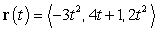 .
.
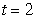 if
if 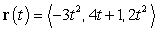 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
76
A particle moves so that 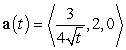 ,
, 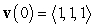 , and
, and 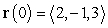 . The location of the particle at time
. The location of the particle at time 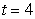 is:
is:
A)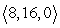 .
.
B)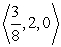 .
.
C)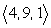 .
.
D)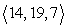 .
.
E) The data are not sufficient to give an answer.
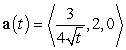 ,
, 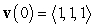 , and
, and 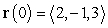 . The location of the particle at time
. The location of the particle at time 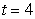 is:
is:A)
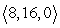 .
.B)
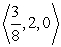 .
.C)
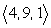 .
.D)
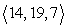 .
.E) The data are not sufficient to give an answer.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
77
A particle moves along the curve 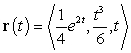 .
.
Decompose the acceleration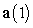 into tangential and normal components.
into tangential and normal components.
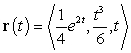 .
.Decompose the acceleration
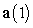 into tangential and normal components.
into tangential and normal components.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate 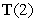 for the parametrization
for the parametrization 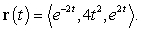
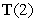 for the parametrization
for the parametrization 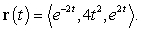

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
79
A particle has acceleration 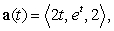 initial velocity
initial velocity 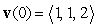 , and initial position
, and initial position 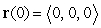 . Decompose
. Decompose 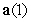 into tangential and normal components.
into tangential and normal components.
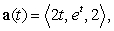 initial velocity
initial velocity 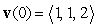 , and initial position
, and initial position 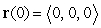 . Decompose
. Decompose 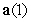 into tangential and normal components.
into tangential and normal components.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
80
A path is parametrized by 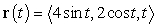 . Find the curvature of the path at the point
. Find the curvature of the path at the point 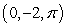 .
.
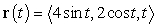 . Find the curvature of the path at the point
. Find the curvature of the path at the point 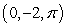 .
.
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck


