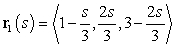Exam 14: Calculus of Vector-Valued Functions
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
A particle has acceleration 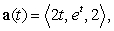 initial velocity
initial velocity 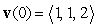 , and initial position
, and initial position 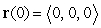 . Decompose
. Decompose 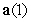 into tangential and normal components.
into tangential and normal components.
Free
(Essay)
4.7/5  (42)
(42)
Correct Answer:
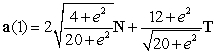
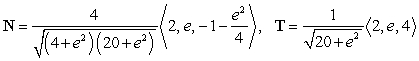
Particle 1 and Particle 2 are flying through space. At time 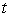 , the position of Particle 1 is given by
, the position of Particle 1 is given by 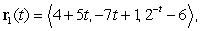 and the position of Particle 2 is given by
and the position of Particle 2 is given by 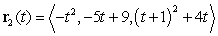 . Do the particles ever collide? If so, where?
. Do the particles ever collide? If so, where?
Free
(Short Answer)
4.9/5  (43)
(43)
Correct Answer:
The particles never collide.
Find the speed at time 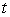 of the particle that is traveling along the curve
of the particle that is traveling along the curve 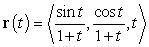 .
.
(Essay)
4.9/5  (40)
(40)
Let 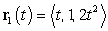 and
and 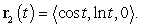 A) Compute
A) Compute 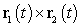 and then differentiate the resulting function.
B) Find
and then differentiate the resulting function.
B) Find 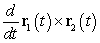 using the cross-product rule for differentiation.
using the cross-product rule for differentiation.
(Essay)
5.0/5  (34)
(34)
A projectile is fired from the ground at an angle of 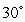 with an initial speed of
with an initial speed of 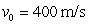 . How far does the projectile travel in the horizontal direction? Recall that
. How far does the projectile travel in the horizontal direction? Recall that 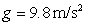 is the acceleration due to gravity on the Earth's surface. Approximate your answer to the nearest tenth of a kilometer.
is the acceleration due to gravity on the Earth's surface. Approximate your answer to the nearest tenth of a kilometer.
(Short Answer)
4.9/5  (37)
(37)
The position of a particle is given by 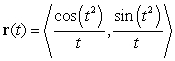 ,
, 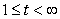 . What is the limit of the particle's speed as
. What is the limit of the particle's speed as 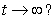
(Essay)
4.7/5  (32)
(32)
Find the curve traced by the following vector valued function and describe it with a Cartesian equation. 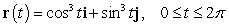
(Essay)
4.8/5  (39)
(39)
If a shuttle orbits about 300 km from the surface of Earth and Earth's radius is 6500 km, how long would it take for the shuttle to go around Earth? Approximate your answer to the nearest hundredth of an hour. (The orbital distance is measured from the center of Earth, and the mass of Earth is 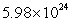 kg.) Recall
kg.) Recall 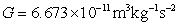 .
.
(Short Answer)
5.0/5  (31)
(31)
A particle moves along the curve 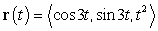 . Compute the velocity and acceleration vectors at
. Compute the velocity and acceleration vectors at 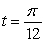 .
.
(Essay)
4.9/5  (37)
(37)
A particle moves along the curve 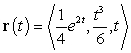 .
Decompose the acceleration
.
Decompose the acceleration 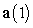 into tangential and normal components.
into tangential and normal components.
(Essay)
4.8/5  (41)
(41)
The path of a certain particle is parametrized by 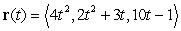 ,
, 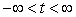 . At what time
. At what time 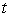 is the minimum speed of the particle achieved?
is the minimum speed of the particle achieved?
(Essay)
4.8/5  (37)
(37)
Showing 1 - 20 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)