Deck 13: Vector Geometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/96
Play
Full screen (f)
Deck 13: Vector Geometry
1
In the triangle 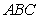 ,
, 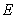 is the midpoint of
is the midpoint of 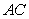 and
and 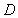 is a point on
is a point on 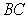 such that
such that 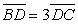 .
. 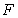 is the intersection of
is the intersection of 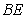 and
and 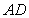 .
. 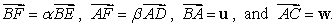
A) Express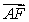 in terms of
in terms of 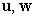 , and
, and 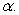
B) Express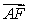 in terms of
in terms of 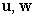 , and
, and 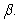
C) Write an equation in terms of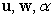 , and
, and 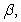 and use the fact that
and use the fact that 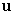 and
and 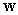 are nonzero, distinct, and nonparallel to find
are nonzero, distinct, and nonparallel to find 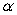 and
and 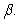
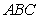 ,
, 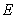 is the midpoint of
is the midpoint of 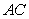 and
and 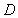 is a point on
is a point on 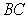 such that
such that 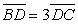 .
. 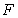 is the intersection of
is the intersection of 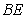 and
and 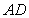 .
. 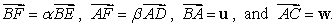
A) Express
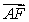 in terms of
in terms of 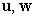 , and
, and 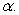
B) Express
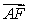 in terms of
in terms of 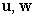 , and
, and 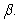
C) Write an equation in terms of
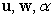 , and
, and 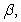 and use the fact that
and use the fact that 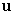 and
and 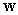 are nonzero, distinct, and nonparallel to find
are nonzero, distinct, and nonparallel to find 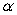 and
and 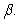
A) 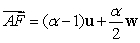 B)
B) 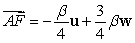 C)
C) 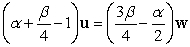
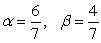
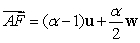 B)
B) 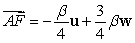 C)
C) 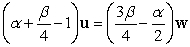
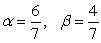
2
Let 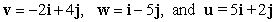 . Calculate the following.
. Calculate the following. 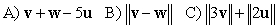
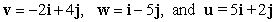 . Calculate the following.
. Calculate the following. 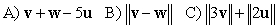
A) 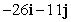 B)
B) 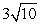 C)
C) 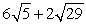
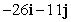 B)
B) 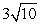 C)
C) 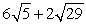
3
Find the point of intersection 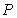 of the three medians in the triangle with vertices
of the three medians in the triangle with vertices 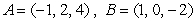 , and
, and 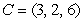 .
.
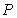 of the three medians in the triangle with vertices
of the three medians in the triangle with vertices 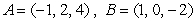 , and
, and 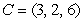 .
.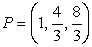
4
Find 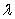 for which
for which 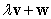 is parallel to
is parallel to 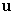 where
where 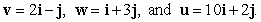
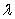 for which
for which 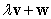 is parallel to
is parallel to 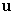 where
where 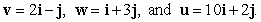

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
5
Express 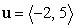 as a linear combination of the two vectors
as a linear combination of the two vectors 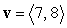 and
and 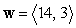 .
.
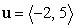 as a linear combination of the two vectors
as a linear combination of the two vectors 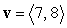 and
and 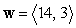 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
6
On a two-dimensional Cartesian coordinate system, 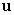 is the position vector from the origin to the point
is the position vector from the origin to the point 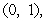 and
and 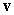 is the position vector with length
is the position vector with length 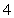 at an angle
at an angle 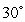 to the positive x-axis. Find the vectors.
to the positive x-axis. Find the vectors.
A)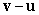
B)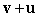
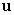 is the position vector from the origin to the point
is the position vector from the origin to the point 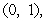 and
and 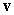 is the position vector with length
is the position vector with length 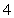 at an angle
at an angle 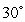 to the positive x-axis. Find the vectors.
to the positive x-axis. Find the vectors. A)
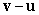
B)
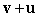

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
7
Find scalars 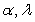 , and
, and 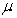 such that:
such that:
A)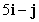 is parallel to
is parallel to 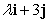 .
.
B)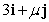 has the same length as
has the same length as 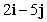 .
.
C)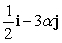 is a unit vector.
is a unit vector.
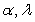 , and
, and 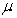 such that:
such that: A)
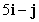 is parallel to
is parallel to 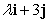 .
. B)
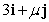 has the same length as
has the same length as 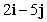 .
. C)
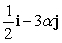 is a unit vector.
is a unit vector.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the pentagon below. 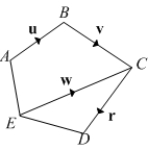
A) Find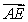 in terms of
in terms of 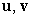 , and
, and 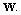
B) Find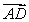 in terms of
in terms of 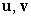 , and
, and 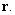
C) Find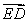 in terms of
in terms of 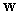 and
and 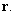

A) Find
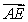 in terms of
in terms of 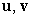 , and
, and 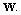
B) Find
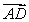 in terms of
in terms of 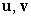 , and
, and 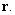
C) Find
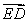 in terms of
in terms of 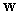 and
and 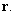

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
9
In the parallelogram 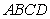 , shown in the figure below, the following holds.
, shown in the figure below, the following holds. 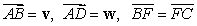
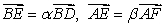
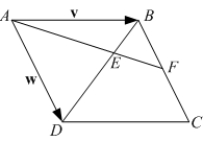
A) Write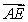 in terms of
in terms of 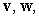 and
and 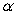 .
.
B) Write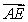 in terms of
in terms of 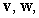 and
and 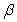 .
.
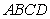 , shown in the figure below, the following holds.
, shown in the figure below, the following holds. 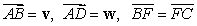
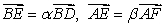

A) Write
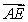 in terms of
in terms of 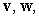 and
and 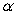 .
. B) Write
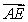 in terms of
in terms of 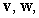 and
and 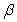 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
10
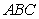 is a triangle and
is a triangle and 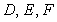 are the midpoints of
are the midpoints of 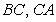 , and
, and 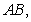 respectively.
respectively. 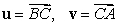
A) Find the vectors
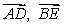 , and
, and 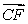 in terms of
in terms of 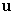 and
and 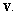
B) Compute the sum of the vectors in (A).

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
11
Express 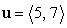 as a linear combination of the two vectors
as a linear combination of the two vectors 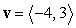 and
and 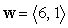 .
.
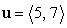 as a linear combination of the two vectors
as a linear combination of the two vectors 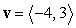 and
and 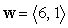 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
12
In the triangle with vertices 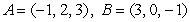 , and
, and 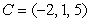 ,
, 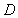 is a point on the side
is a point on the side 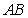 , such that
, such that 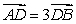 .
. 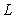 is a line through
is a line through 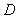 , parallel to the side
, parallel to the side 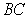 , intersecting
, intersecting 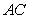 at a point
at a point 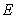 .
.
A) Find the vector equation of the line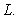
B) Compute the length of the vector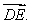
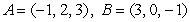 , and
, and 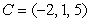 ,
, 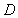 is a point on the side
is a point on the side 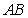 , such that
, such that 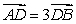 .
. 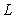 is a line through
is a line through 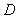 , parallel to the side
, parallel to the side 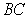 , intersecting
, intersecting 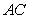 at a point
at a point 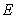 .
. A) Find the vector equation of the line
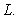
B) Compute the length of the vector
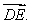

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
13
Let 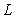 be the line
be the line 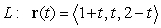 .
.
A) Find the distance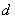 between any point on
between any point on 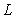 and the origin as a function of
and the origin as a function of 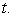
B) Find the point on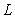 closest to the origin by minimizing
closest to the origin by minimizing 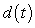 .
.
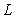 be the line
be the line 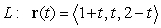 .
. A) Find the distance
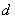 between any point on
between any point on 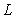 and the origin as a function of
and the origin as a function of 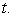
B) Find the point on
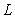 closest to the origin by minimizing
closest to the origin by minimizing 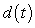 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the following two lines. 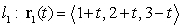
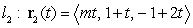 The two lines intersect if:
The two lines intersect if:
A)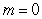 .
.
B)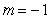 .
.
C)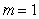 .
.
D)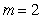 .
.
E)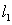 and
and 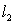 do not intersect for any value of
do not intersect for any value of 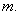
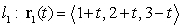
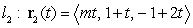 The two lines intersect if:
The two lines intersect if:A)
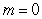 .
.B)
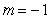 .
.C)
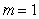 .
.D)
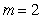 .
.E)
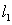 and
and 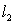 do not intersect for any value of
do not intersect for any value of 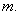

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
15
Two different nonzero vectors, 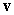 and
and 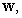 that are not parallel satisfy the equality
that are not parallel satisfy the equality 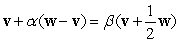 , where
, where 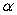 and
and 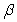 are scalars.
are scalars.
Find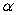 and
and 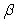 .
.
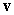 and
and 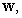 that are not parallel satisfy the equality
that are not parallel satisfy the equality 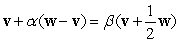 , where
, where 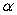 and
and 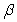 are scalars.
are scalars.Find
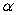 and
and 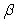 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
16
Let 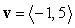 . Find the vector
. Find the vector 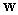 such that
such that 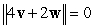 .
.
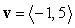 . Find the vector
. Find the vector 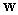 such that
such that 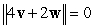 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
17
Let 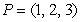 and
and 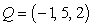 .
.
A) Write the coordinates of the point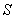 on
on 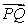 lying three-fifths of the way from
lying three-fifths of the way from 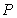 to
to 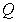 .
.
B) Write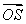 as a linear combination of
as a linear combination of 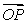 and
and 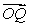 .
.
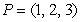 and
and 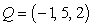 .
. A) Write the coordinates of the point
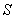 on
on 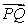 lying three-fifths of the way from
lying three-fifths of the way from 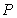 to
to 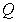 .
. B) Write
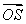 as a linear combination of
as a linear combination of 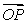 and
and 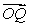 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
18
Express 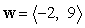 as a linear combination of
as a linear combination of 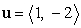 and
and 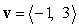 .
.
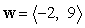 as a linear combination of
as a linear combination of 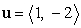 and
and 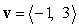 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
19
Find 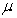 and
and 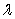 such that
such that 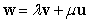 is a unit vector parallel to
is a unit vector parallel to  where
where 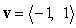 and
and  .
.
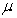 and
and 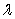 such that
such that 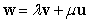 is a unit vector parallel to
is a unit vector parallel to 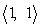 where
where 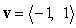 and
and  .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the four points 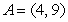 ,
, 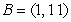 ,
, 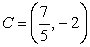 , and
, and 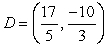 . Are
. Are 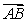 and
and 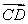 parallel, and if so, do they point in the same direction?
parallel, and if so, do they point in the same direction?
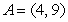 ,
, 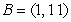 ,
, 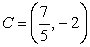 , and
, and 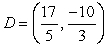 . Are
. Are 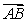 and
and 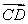 parallel, and if so, do they point in the same direction?
parallel, and if so, do they point in the same direction?
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
21
Find the decomposition 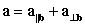 of
of 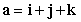 with respect to
with respect to 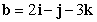 .
.
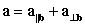 of
of 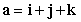 with respect to
with respect to 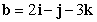 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
22
The two lines 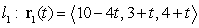 and
and 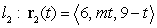 intersect if:
intersect if:
A)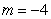 .
.
B)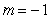 .
.
C)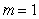 .
.
D)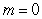 .
.
E)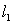 and
and 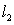 do not intersect for any value of
do not intersect for any value of 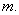
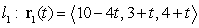 and
and 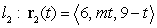 intersect if:
intersect if:A)
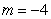 .
.B)
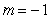 .
.C)
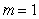 .
.D)
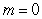 .
.E)
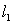 and
and 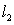 do not intersect for any value of
do not intersect for any value of 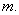

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
23
Find the decomposition 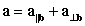 of
of 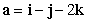 with respect to
with respect to 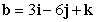 .
.
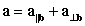 of
of 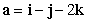 with respect to
with respect to 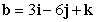 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
24
Find an equation of the line that passes through the points 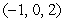 and
and 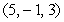 .
.
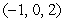 and
and 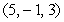 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
25
Find a unit vector 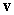 orthogonal to
orthogonal to 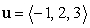 and making an angle of
and making an angle of 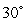 with the vector
with the vector 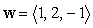 .
.
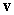 orthogonal to
orthogonal to 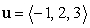 and making an angle of
and making an angle of 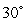 with the vector
with the vector 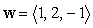 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
26
Let 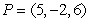 and
and 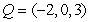 . Find the point on
. Find the point on 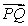 lying three-fifths of the way from
lying three-fifths of the way from 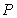 to
to 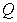 .
.
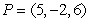 and
and 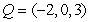 . Find the point on
. Find the point on 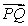 lying three-fifths of the way from
lying three-fifths of the way from 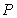 to
to 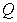 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
27
Find the decomposition 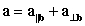 of
of 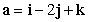 with respect to
with respect to 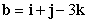 .
.
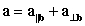 of
of 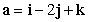 with respect to
with respect to 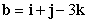 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
28
Find an equation of the line that passes through the points 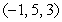 and
and 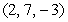 .
.
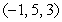 and
and 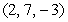 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
29
Find a scalar 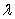 such that the vectors
such that the vectors 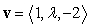 and
and 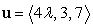 are orthogonal.
are orthogonal.
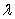 such that the vectors
such that the vectors 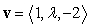 and
and 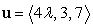 are orthogonal.
are orthogonal.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the points 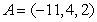 ,
, 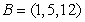 ,
, 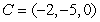 , and
, and 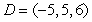 . Find the length of the vector starting at the midpoint of
. Find the length of the vector starting at the midpoint of 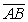 and ending at the midpoint of
and ending at the midpoint of 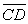 .
.
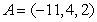 ,
, 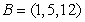 ,
, 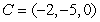 , and
, and 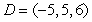 . Find the length of the vector starting at the midpoint of
. Find the length of the vector starting at the midpoint of 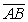 and ending at the midpoint of
and ending at the midpoint of 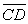 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
31
The decomposition 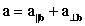 of
of 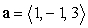 with respect to
with respect to 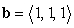 is which of the following?
is which of the following?
A)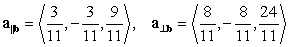
B)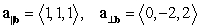
C)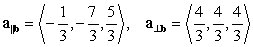
D)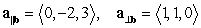
E)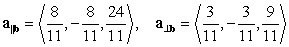
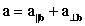 of
of 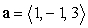 with respect to
with respect to 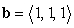 is which of the following?
is which of the following?A)
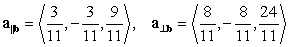
B)
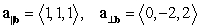
C)
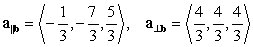
D)
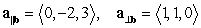
E)
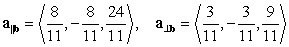

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
32
The angle between 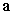 and
and 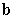 is
is 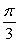 and
and 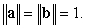 Let
Let 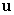 and
and 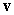 be the vectors
be the vectors 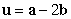 and
and 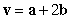 .
.
A) Find the dot product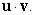
B) Find the dot product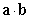 and use it to compute the lengths
and use it to compute the lengths 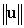 and
and 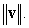
C) Find the angle between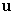 and
and 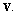
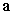 and
and 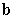 is
is 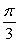 and
and 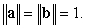 Let
Let 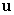 and
and 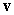 be the vectors
be the vectors 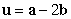 and
and 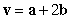 .
. A) Find the dot product
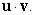
B) Find the dot product
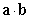 and use it to compute the lengths
and use it to compute the lengths 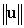 and
and 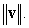
C) Find the angle between
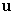 and
and 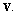

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
33
Find the angle between the vectors 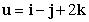 and
and 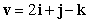 .
.
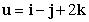 and
and 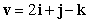 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
34
Find an equation of the bisector 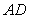 of the angle
of the angle 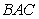 in the triangle with vertices
in the triangle with vertices 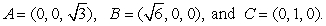
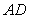 of the angle
of the angle 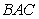 in the triangle with vertices
in the triangle with vertices 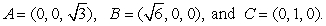

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
35
The angle between the vectors 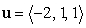 and
and 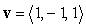 is:
is:
A)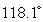 .
.
B)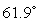 .
.
C)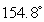 .
.
D)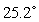 .
.
E)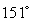 .
.
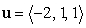 and
and 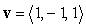 is:
is:A)
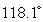 .
.B)
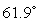 .
.C)
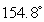 .
.D)
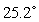 .
.E)
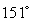 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
36
The two lines 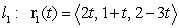 and
and 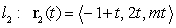 intersect if:
intersect if:
A)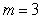 .
.
B)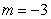 .
.
C)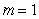 .
.
D)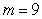 .
.
E)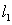 and
and 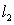 do not intersect for any value of
do not intersect for any value of 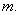
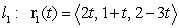 and
and 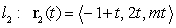 intersect if:
intersect if:A)
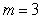 .
.B)
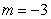 .
.C)
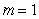 .
.D)
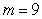 .
.E)
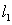 and
and 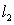 do not intersect for any value of
do not intersect for any value of 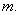

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
37
In the triangle with vertices 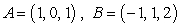 , and
, and 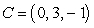 ,
, 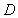 is a point on
is a point on 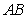 such that
such that 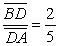 .
. 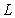 is a line through
is a line through 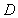 , parallel to
, parallel to 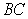 and intersecting
and intersecting 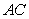 at point
at point 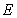 .
.
A) Find a vector equation of the line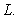
B) Find the length of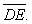
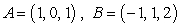 , and
, and 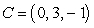 ,
, 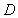 is a point on
is a point on 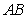 such that
such that 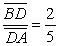 .
.  is a line through
is a line through  , parallel to
, parallel to 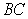 and intersecting
and intersecting 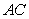 at point
at point 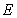 .
. A) Find a vector equation of the line
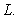
B) Find the length of
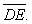

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
38
Determine whether the lines 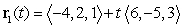 and
and 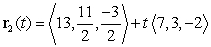 intersect, and if so, find the point of intersection.
intersect, and if so, find the point of intersection.
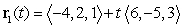 and
and 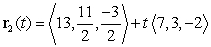 intersect, and if so, find the point of intersection.
intersect, and if so, find the point of intersection.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
39
The angle between two intersecting lines is the acute angle between the direction vectors of the lines. Find the angle between the line through the points 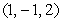 and
and 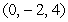 and the line through the points
and the line through the points 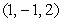 and
and 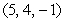 .
.
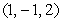 and
and 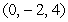 and the line through the points
and the line through the points 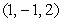 and
and 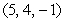 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
40
Find an equation of the line that passes through 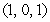 and is orthogonal to the vectors
and is orthogonal to the vectors 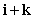 and
and 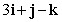 .
.
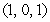 and is orthogonal to the vectors
and is orthogonal to the vectors 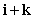 and
and 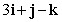 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
41
What is the minimum force you must apply to pull a 35-kg mass up a frictionless ramp, inclined at an angle 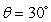 ?
?
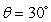 ?
?
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the parallel lines 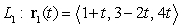 and
and 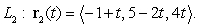 Compute the distance
Compute the distance 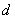 between the two lines using the following steps.
between the two lines using the following steps.
A) Choose any two points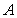 and
and 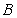 on
on 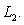
B) Choose any point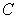 on
on 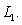
C) Compute the area of the triangle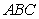 , the length of
, the length of 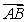 , and find the height from
, and find the height from 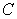 to
to 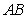 , using the area of a triangle.
, using the area of a triangle.
D) What is the distance between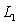 and
and 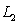 ?
?
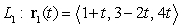 and
and 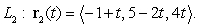 Compute the distance
Compute the distance 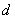 between the two lines using the following steps.
between the two lines using the following steps. A) Choose any two points
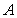 and
and 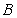 on
on 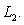
B) Choose any point
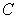 on
on 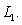
C) Compute the area of the triangle
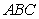 , the length of
, the length of 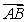 , and find the height from
, and find the height from 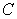 to
to 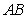 , using the area of a triangle.
, using the area of a triangle. D) What is the distance between
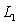 and
and 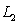 ?
?
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
43
Compute the height 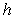 to the side
to the side 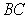 in the triangle with vertices at
in the triangle with vertices at 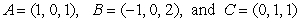 .
.
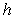 to the side
to the side 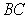 in the triangle with vertices at
in the triangle with vertices at 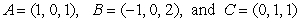 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
44
Compute the area of the projection of the parallelogram with vertices 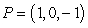 ,
, 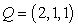 ,
, 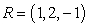 , and
, and 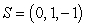 on the xy-plane.
on the xy-plane.
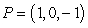 ,
, 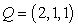 ,
, 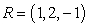 , and
, and 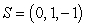 on the xy-plane.
on the xy-plane.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
45
The height 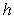 of the triangle
of the triangle 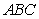 shown in the figure is which of the following?
shown in the figure is which of the following? 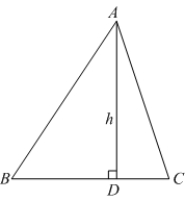
A)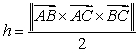
B)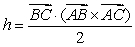
C)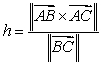
D)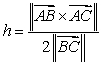
E) none of the above.
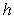 of the triangle
of the triangle  shown in the figure is which of the following?
shown in the figure is which of the following? 
A)
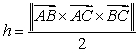
B)
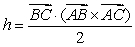
C)
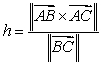
D)
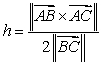
E) none of the above.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
46
Find all the vectors 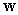 of length
of length 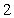 that are orthogonal to the vectors
that are orthogonal to the vectors 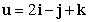 and
and 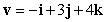 .
.
 of length
of length 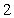 that are orthogonal to the vectors
that are orthogonal to the vectors 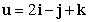 and
and 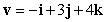 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
47
Determine whether the vectors 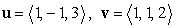 , and
, and 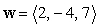 lie in one plane.
lie in one plane.
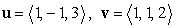 , and
, and 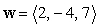 lie in one plane.
lie in one plane.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
48
Let 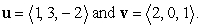
A) Find the area of the parallelogram spanned by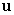 and
and 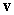 .
.
B) Find a vector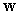 orthogonal to
orthogonal to 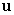 and
and 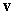 so that the volume of the parallelepiped spanned by
so that the volume of the parallelepiped spanned by 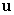 ,
, 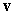 , and
, and 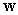 is
is 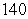 .
.
A) Find the area of the parallelogram spanned by
 and
and  .
. B) Find a vector
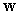 orthogonal to
orthogonal to 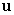 and
and 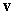 so that the volume of the parallelepiped spanned by
so that the volume of the parallelepiped spanned by 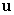 ,
, 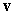 , and
, and 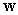 is
is 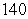 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
49
Find the volume of the parallelepiped with vertices at 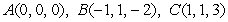 , and
, and 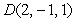 .
.
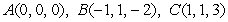 , and
, and 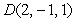 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
50
The angle between two intersecting lines is the acute angle between the direction vectors of the lines. Find the angle between the line through the points 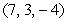 and
and 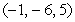 and the line through the points
and the line through the points 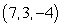 and
and 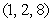 .
.
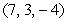 and
and 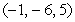 and the line through the points
and the line through the points 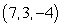 and
and 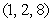 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
51
The line 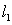 is determined by the two points
is determined by the two points 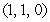 and
and 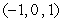 , and the line
, and the line 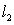 is determined by the points
is determined by the points 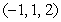 and
and 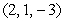 . Find the unit vectors
. Find the unit vectors 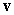 along the line perpendicular to both
along the line perpendicular to both 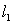 and
and 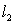 .
.
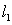 is determined by the two points
is determined by the two points 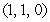 and
and 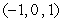 , and the line
, and the line 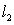 is determined by the points
is determined by the points 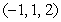 and
and 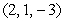 . Find the unit vectors
. Find the unit vectors 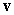 along the line perpendicular to both
along the line perpendicular to both 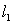 and
and 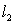 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
52
Calculate the volume of the parallelepiped spanned by 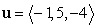 ,
, 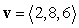 , and
, and 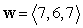 .
.
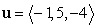 ,
, 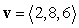 , and
, and 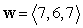 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
53
Compute the area of the projection onto the xy-plane of the parallelogram spanned by the vectors 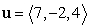 and
and 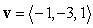 .
.
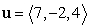 and
and 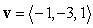 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following lines 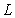 is parallel to the plane
is parallel to the plane 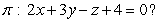
A)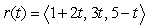
B)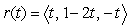
C)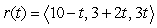
D)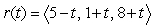
E)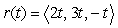
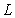 is parallel to the plane
is parallel to the plane 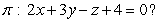
A)
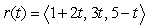
B)
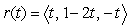
C)
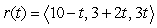
D)
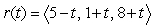
E)
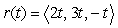

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
55
Let 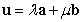 and
and 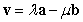 be two nonzero orthogonal vectors.
be two nonzero orthogonal vectors.
A) Find in terms of
in terms of 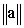 ,
, 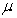 , and
, and 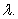
B) Find the scalar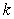 such that
such that 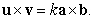
C) If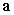 and
and 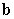 are orthogonal unit vectors, write the area of the parallelogram spanned by
are orthogonal unit vectors, write the area of the parallelogram spanned by 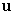 and
and 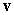 in terms of
in terms of 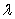 only.
only.
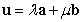 and
and 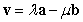 be two nonzero orthogonal vectors.
be two nonzero orthogonal vectors. A) Find
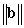 in terms of
in terms of 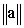 ,
, 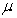 , and
, and 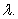
B) Find the scalar
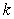 such that
such that 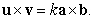
C) If
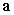 and
and 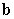 are orthogonal unit vectors, write the area of the parallelogram spanned by
are orthogonal unit vectors, write the area of the parallelogram spanned by 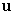 and
and 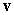 in terms of
in terms of 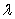 only.
only.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
56
Compute the height 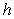 to the side
to the side 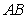 in the triangle with vertices at
in the triangle with vertices at 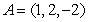 ,
, 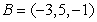 , and
, and 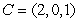 .
.
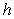 to the side
to the side 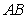 in the triangle with vertices at
in the triangle with vertices at 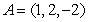 ,
, 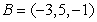 , and
, and 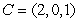 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
57
The line 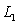 is determined by the points
is determined by the points 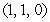 and
and 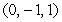 .
.
The line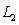 is determined by the points
is determined by the points 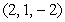 and
and 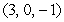 .
.
Find a unit vector along the line perpendicular to both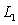 and
and 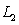 .
.
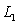 is determined by the points
is determined by the points 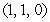 and
and 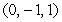 .
.The line
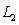 is determined by the points
is determined by the points 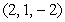 and
and 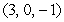 .
.Find a unit vector along the line perpendicular to both
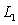 and
and 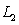 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
58
The line 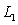 is determined by the two points
is determined by the two points 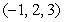 and
and 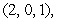 and the line
and the line 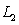 is determined by the points
is determined by the points 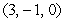 and
and 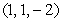 . Find a unit vector along the line perpendicular to both
. Find a unit vector along the line perpendicular to both 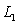 and
and 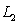 .
.
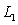 is determined by the two points
is determined by the two points 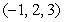 and
and 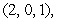 and the line
and the line 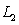 is determined by the points
is determined by the points 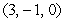 and
and 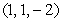 . Find a unit vector along the line perpendicular to both
. Find a unit vector along the line perpendicular to both 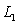 and
and 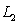 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
59
Find the projection of 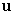 along
along 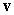 if
if 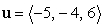 and
and 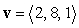 .
.
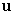 along
along 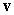 if
if 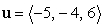 and
and 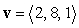 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
60
For the plane 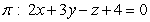 and the line
and the line 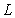 :
: 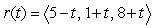 , find the scalar form of the equation of the plane
, find the scalar form of the equation of the plane 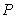 that contains
that contains 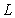 and is orthogonal to
and is orthogonal to 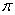 .
.
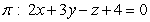 and the line
and the line 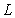 :
: 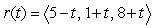 , find the scalar form of the equation of the plane
, find the scalar form of the equation of the plane 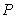 that contains
that contains 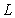 and is orthogonal to
and is orthogonal to 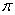 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
61
Find an equation of the plane passing through the points 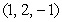 and
and 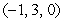 and with the vector
and with the vector 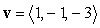 lying on the plane.
lying on the plane.
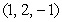 and
and 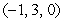 and with the vector
and with the vector 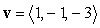 lying on the plane.
lying on the plane.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
62
Describe the trace obtained by intersecting the quadric surface 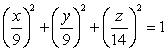 with the plane
with the plane 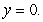
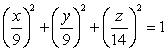 with the plane
with the plane 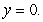

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
63
Find an equation of the plane with traces 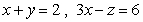 , and
, and 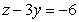 in the
in the 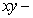 plane,
plane, 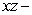 plane, and
plane, and 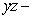 plane, respectively.
plane, respectively.
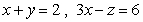 , and
, and 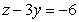 in the
in the 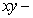 plane,
plane, 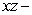 plane, and
plane, and 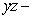 plane, respectively.
plane, respectively.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
64
For which values of 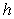 is the intersection of the horizontal plane
is the intersection of the horizontal plane 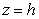 and the hyperboloid
and the hyperboloid 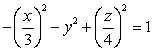 empty?
empty?
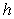 is the intersection of the horizontal plane
is the intersection of the horizontal plane 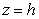 and the hyperboloid
and the hyperboloid 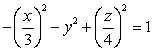 empty?
empty?
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
65
Find an equation of the plane passing through the points 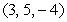 and
and 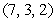 , and parallel to any line with the direction vector
, and parallel to any line with the direction vector 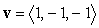 .
.
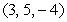 and
and 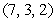 , and parallel to any line with the direction vector
, and parallel to any line with the direction vector 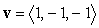 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
66
Write the equation of the quadric surface 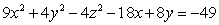 in standard form, and identify the type of the quadric conic.
in standard form, and identify the type of the quadric conic.
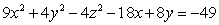 in standard form, and identify the type of the quadric conic.
in standard form, and identify the type of the quadric conic.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
67
Let 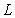 be the line
be the line 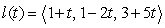 and
and 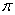 be the plane
be the plane 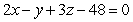 .
.
A) Find the point of intersection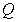 of
of 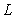 and
and 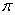 .
.
B) Find an equation of the plane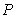 (in scalar form) that passes through the point
(in scalar form) that passes through the point 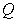 and is orthogonal to
and is orthogonal to 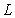 .
.
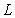 be the line
be the line 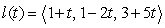 and
and 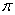 be the plane
be the plane 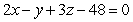 .
. A) Find the point of intersection
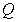 of
of 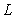 and
and 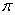 .
. B) Find an equation of the plane
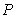 (in scalar form) that passes through the point
(in scalar form) that passes through the point 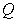 and is orthogonal to
and is orthogonal to 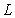 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
68
Write the equation of the quadric surface 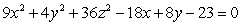 in standard form, and identify its type.
in standard form, and identify its type.
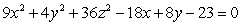 in standard form, and identify its type.
in standard form, and identify its type.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
69
The following lines (  is a parameter) are known to be in one plane.
is a parameter) are known to be in one plane. 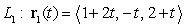
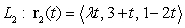 If they intersect at the point
If they intersect at the point 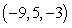 , find the following.
, find the following.
A) the value of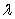
B) the scalar equation of the plane
 is a parameter) are known to be in one plane.
is a parameter) are known to be in one plane. 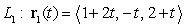
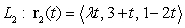 If they intersect at the point
If they intersect at the point 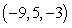 , find the following.
, find the following. A) the value of
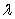
B) the scalar equation of the plane

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the 3 lines. 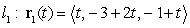
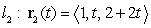
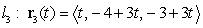 Which of the following statements is correct?
Which of the following statements is correct?
A) The three lines are parallel.
B) The three lines lie in one plane and do not intersect at one point.
C) The three lines are not contained in one plane.
D) The three lines lie in one plane and they intersect at one point.
E) Two of the lines are parallel.
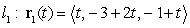
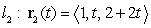
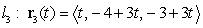 Which of the following statements is correct?
Which of the following statements is correct?A) The three lines are parallel.
B) The three lines lie in one plane and do not intersect at one point.
C) The three lines are not contained in one plane.
D) The three lines lie in one plane and they intersect at one point.
E) Two of the lines are parallel.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
71
Let 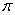 and
and 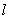 be the plane and line determined by the following equations
be the plane and line determined by the following equations 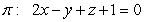
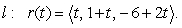 Find the equation of the line
Find the equation of the line 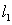 passing through the intersection point of
passing through the intersection point of 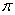 and
and 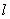 and parallel to the trace of
and parallel to the trace of 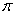 in the
in the 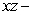 plane.
plane.
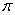 and
and 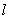 be the plane and line determined by the following equations
be the plane and line determined by the following equations 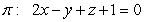
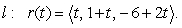 Find the equation of the line
Find the equation of the line 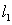 passing through the intersection point of
passing through the intersection point of 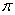 and
and 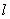 and parallel to the trace of
and parallel to the trace of 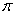 in the
in the 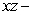 plane.
plane.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
72
Find an equation of the plane with traces 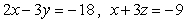 , and
, and 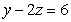 in the
in the 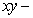 plane,
plane, 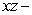 plane, and
plane, and 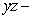 plane, respectively.
plane, respectively.
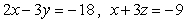 , and
, and 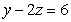 in the
in the 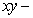 plane,
plane, 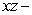 plane, and
plane, and 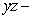 plane, respectively.
plane, respectively.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
73
For which values of h is the intersection of the horizontal plane 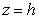 and the ellipsoid
and the ellipsoid 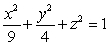 empty?
empty?
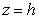 and the ellipsoid
and the ellipsoid 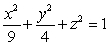 empty?
empty?
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
74
Write the equation of the quadric surface 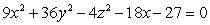 in standard form, and identify its type.
in standard form, and identify its type.
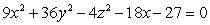 in standard form, and identify its type.
in standard form, and identify its type.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
75
Identify the quadric surface 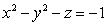 .
.
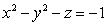 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
76
Describe the trace obtained by intersecting the quadric surface 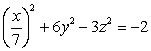 with the plane
with the plane 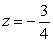 .
.
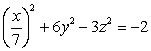 with the plane
with the plane 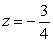 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
77
Find an equation of the plane that passes through the points 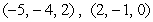 , and
, and 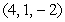 .
.
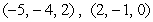 , and
, and 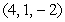 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
78
Find an equation of the plane that passes through the points 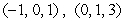 , and
, and 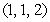 .
.
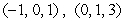 , and
, and 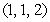 .
.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
79
Three nonzero vectors, 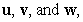 in 3-space are in one plane (coplanar) if:
in 3-space are in one plane (coplanar) if:
A)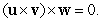
B) one of them is a linear combination of the other two.
C) one of them is parallel to the cross product of the other two.
D) the scalar triple product of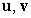 , and
, and 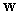 is zero.
is zero.
E) both B and D.
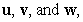 in 3-space are in one plane (coplanar) if:
in 3-space are in one plane (coplanar) if:A)
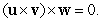
B) one of them is a linear combination of the other two.
C) one of them is parallel to the cross product of the other two.
D) the scalar triple product of
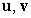 , and
, and 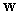 is zero.
is zero.E) both B and D.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
80
The plane 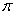 is determined by the points
is determined by the points 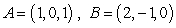 , and
, and 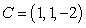 .
. 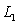 is the trace of
is the trace of 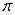 in the xy-plane.
in the xy-plane. 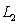 is the line
is the line 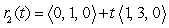 .
.
Which of the following statements is correct?
A)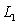 and
and 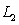 intersect.
intersect.
B)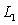 and
and 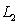 are parallel.
are parallel.
C)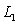 and
and 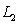 do not lie in one plane.
do not lie in one plane.
D) There is not enough data to conclude about the mutual position of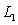 and
and 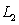 .
.
E)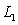 and
and 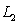 coincide.
coincide.
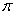 is determined by the points
is determined by the points 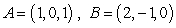 , and
, and 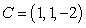 .
. 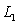 is the trace of
is the trace of 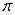 in the xy-plane.
in the xy-plane. 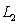 is the line
is the line 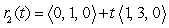 .
.Which of the following statements is correct?
A)
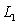 and
and 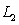 intersect.
intersect.B)
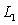 and
and 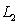 are parallel.
are parallel.C)
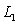 and
and 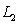 do not lie in one plane.
do not lie in one plane.D) There is not enough data to conclude about the mutual position of
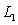 and
and 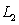 .
.E)
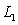 and
and 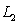 coincide.
coincide.
Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck


