Exam 13: Vector Geometry
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Consider the parallel lines 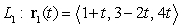 and
and 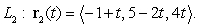 Compute the distance
Compute the distance 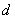 between the two lines using the following steps.
A) Choose any two points
between the two lines using the following steps.
A) Choose any two points 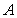 and
and 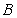 on
on 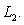 B) Choose any point
B) Choose any point 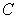 on
on 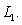 C) Compute the area of the triangle
C) Compute the area of the triangle 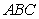 , the length of
, the length of 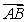 , and find the height from
, and find the height from 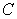 to
to 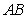 , using the area of a triangle.
D) What is the distance between
, using the area of a triangle.
D) What is the distance between 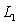 and
and 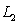 ?
?
Free
(Essay)
4.9/5  (34)
(34)
Correct Answer:
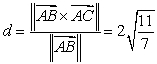
Let 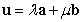 and
and 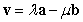 be two nonzero orthogonal vectors.
A) Find
be two nonzero orthogonal vectors.
A) Find 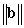 in terms of
in terms of 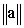 ,
, 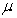 , and
, and 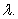 B) Find the scalar
B) Find the scalar 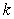 such that
such that 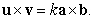 C) If
C) If 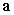 and
and 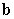 are orthogonal unit vectors, write the area of the parallelogram spanned by
are orthogonal unit vectors, write the area of the parallelogram spanned by 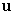 and
and 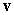 in terms of
in terms of 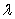 only.
only.
Free
(Essay)
4.9/5  (26)
(26)
Correct Answer:
A) 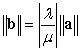 B)
B) 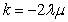 C)
C) 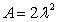
Convert the point 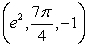 from cylindrical coordinates to rectangular coordinates.
from cylindrical coordinates to rectangular coordinates.
Free
(Essay)
4.9/5  (32)
(32)
Correct Answer:
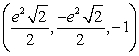
Compute the height 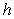 to the side
to the side 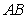 in the triangle with vertices at
in the triangle with vertices at 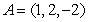 ,
, 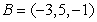 , and
, and 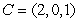 .
.
(Essay)
4.7/5  (33)
(33)
Let 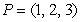 and
and 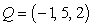 .
A) Write the coordinates of the point
.
A) Write the coordinates of the point 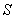 on
on 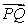 lying three-fifths of the way from
lying three-fifths of the way from 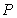 to
to 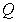 .
B) Write
.
B) Write 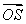 as a linear combination of
as a linear combination of 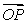 and
and 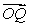 .
.
(Essay)
4.9/5  (32)
(32)
Find scalars 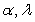 , and
, and 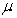 such that:
A)
such that:
A) 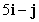 is parallel to
is parallel to 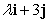 .
B)
.
B) 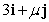 has the same length as
has the same length as 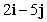 .
C)
.
C) 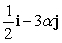 is a unit vector.
is a unit vector.
(Essay)
4.9/5  (32)
(32)
The angle between two intersecting lines is the acute angle between the direction vectors of the lines. Find the angle between the line through the points 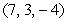 and
and 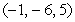 and the line through the points
and the line through the points 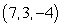 and
and 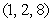 .
.
(Essay)
4.7/5  (33)
(33)
Convert the point 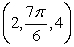 from cylindrical coordinates to spherical coordinates.
from cylindrical coordinates to spherical coordinates.
(Essay)
4.9/5  (36)
(36)
Consider the points 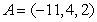 ,
, 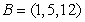 ,
, 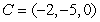 , and
, and 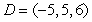 . Find the length of the vector starting at the midpoint of
. Find the length of the vector starting at the midpoint of 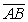 and ending at the midpoint of
and ending at the midpoint of 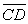 .
.
(Essay)
4.8/5  (32)
(32)
Write the equation of the quadric surface 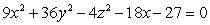 in standard form, and identify its type.
in standard form, and identify its type.
(Essay)
4.8/5  (32)
(32)
The angle between 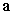 and
and 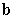 is
is 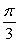 and
and 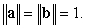 Let
Let 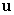 and
and 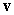 be the vectors
be the vectors 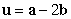 and
and 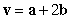 .
A) Find the dot product
.
A) Find the dot product 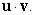 B) Find the dot product
B) Find the dot product 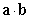 and use it to compute the lengths
and use it to compute the lengths 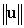 and
and 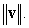 C) Find the angle between
C) Find the angle between 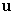 and
and 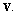
(Essay)
4.8/5  (31)
(31)
On a two-dimensional Cartesian coordinate system, 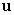 is the position vector from the origin to the point
is the position vector from the origin to the point 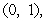 and
and 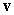 is the position vector with length
is the position vector with length 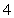 at an angle
at an angle 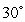 to the positive x-axis. Find the vectors.
A)
to the positive x-axis. Find the vectors.
A) 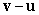 B)
B) 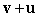
(Essay)
4.8/5  (39)
(39)
Find an equation of the plane passing through the points 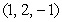 and
and 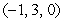 and with the vector
and with the vector 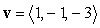 lying on the plane.
lying on the plane.
(Essay)
4.8/5  (29)
(29)
Compute the area of the projection onto the xy-plane of the parallelogram spanned by the vectors 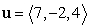 and
and 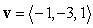 .
.
(Short Answer)
4.9/5  (37)
(37)
Consider the following two lines. 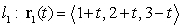
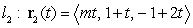 The two lines intersect if:
The two lines intersect if:
(Multiple Choice)
4.7/5  (26)
(26)
Showing 1 - 20 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)