Deck 3: Determining Change: Derivatives
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/48
Play
Full screen (f)
Deck 3: Determining Change: Derivatives
1
Find the derivative of 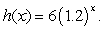
A)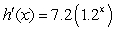
B)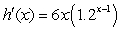
C)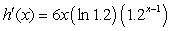
D)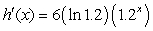
E)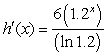
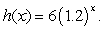
A)
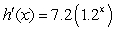
B)
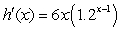
C)
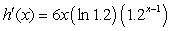
D)
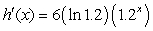
E)
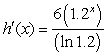
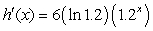
2
Find the derivative of 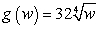 .
.
A)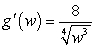
B)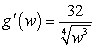
C)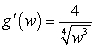
D)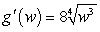
E)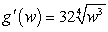
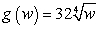 .
.A)
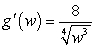
B)
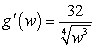
C)
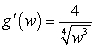
D)
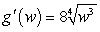
E)
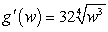
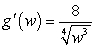
3
The population of Aurora, a Nevada ghost town, can be modeled as 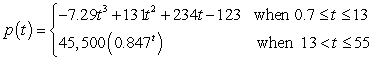 where output is measured in people and t is the number of years since 1859. Write a model for the rate of change of the population of Aurora.
where output is measured in people and t is the number of years since 1859. Write a model for the rate of change of the population of Aurora.
A)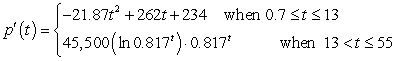 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
B)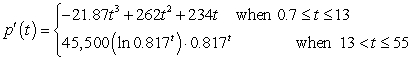 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
C)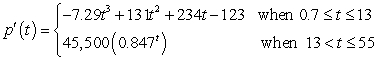 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
D)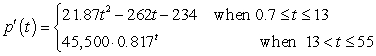 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
E)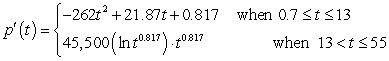 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
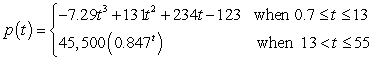 where output is measured in people and t is the number of years since 1859. Write a model for the rate of change of the population of Aurora.
where output is measured in people and t is the number of years since 1859. Write a model for the rate of change of the population of Aurora.A)
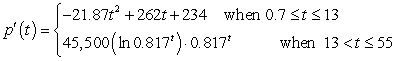 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.B)
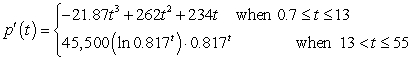 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.C)
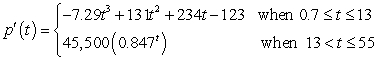 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.D)
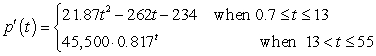 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.E)
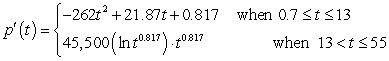 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.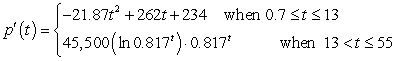 where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859.
where output is measured in people per year gives the rate of change of the population of Aurora, Nevada t years since 1859. 4
Find the derivative of 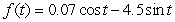 .
.
A)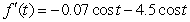
B)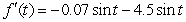
C)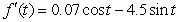
D)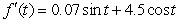
E)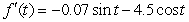
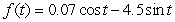 .
.A)
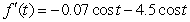
B)
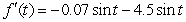
C)
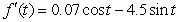
D)
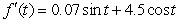
E)
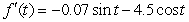

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
5
Find the derivative of 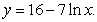
A)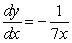
B)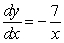
C)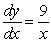
D)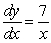
E)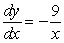
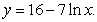
A)
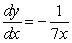
B)
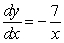
C)
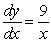
D)
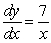
E)
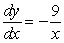

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
6
A publishing company estimates that when a new book by a best-selling American author first hits the market, its sales can be predicted by the equation 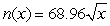 , where
, where 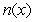 represents the total number (in thousands) of copies of the book sold in the United States by the end of the xth week. The number of copies of the book sold abroad by the end of the xth week can be modeled by
represents the total number (in thousands) of copies of the book sold in the United States by the end of the xth week. The number of copies of the book sold abroad by the end of the xth week can be modeled by 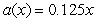 thousand copies of the book How many books will be sold by the end of the first year (that is, 52 weeks)?
thousand copies of the book How many books will be sold by the end of the first year (that is, 52 weeks)?
A) 497,278 books
B) 503,778 books
C) 6,500 books
D) 490,778 books
E) 4,907 books
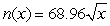 , where
, where 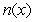 represents the total number (in thousands) of copies of the book sold in the United States by the end of the xth week. The number of copies of the book sold abroad by the end of the xth week can be modeled by
represents the total number (in thousands) of copies of the book sold in the United States by the end of the xth week. The number of copies of the book sold abroad by the end of the xth week can be modeled by 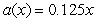 thousand copies of the book How many books will be sold by the end of the first year (that is, 52 weeks)?
thousand copies of the book How many books will be sold by the end of the first year (that is, 52 weeks)?A) 497,278 books
B) 503,778 books
C) 6,500 books
D) 490,778 books
E) 4,907 books

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
7
The graph below gives membership in an organization during its first year. Estimate the instantaneous rate of change in membership in September. 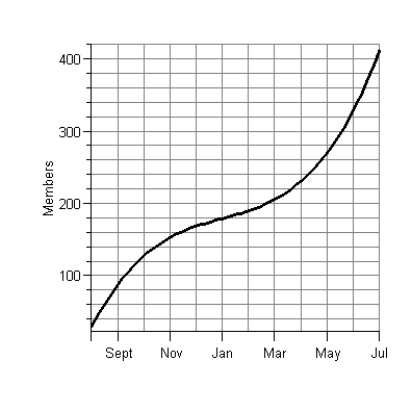
A) 48 members per month
B) 12 members per month
C) 89 members per month
D) 96 members per month
E) 32 members per month

A) 48 members per month
B) 12 members per month
C) 89 members per month
D) 96 members per month
E) 32 members per month

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
8
Find 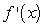 of
of 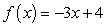 by using the definition of the derivative.
by using the definition of the derivative.
A)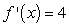
B)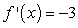
C)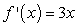
D)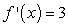
E)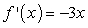
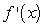 of
of 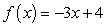 by using the definition of the derivative.
by using the definition of the derivative.A)
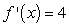
B)
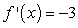
C)
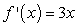
D)
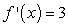
E)
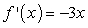

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
9
Find the derivative of 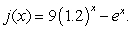
A)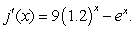
B)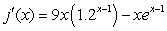
C)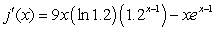
D)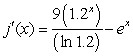
E)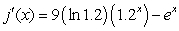
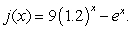
A)
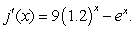
B)
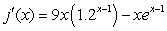
C)
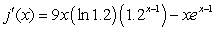
D)
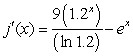
E)
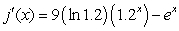

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
10
Find the derivative of 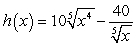 .
.
A)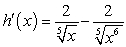
B)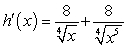
C)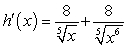
D)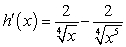
E)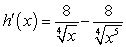
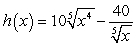 .
.A)
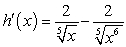
B)
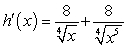
C)
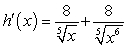
D)
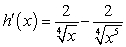
E)
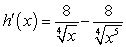

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
11
Find the derivative of 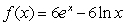 .
.
A)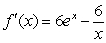
B)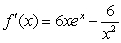
C)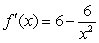
D)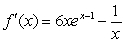
E)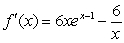
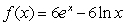 .
.A)
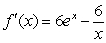
B)
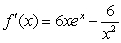
C)
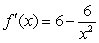
D)
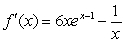
E)
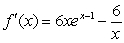

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
12
The future value that accrues when $900 is invested at 7%, compounded continuously, is 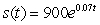 , where t is the number of years. At what rate is the money in this account growing when
, where t is the number of years. At what rate is the money in this account growing when 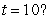
A) $18.12 per year
B) $69.63 per year
C) $1812.38 per year
D) $965.26 per year
E) $126.87 per year
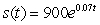 , where t is the number of years. At what rate is the money in this account growing when
, where t is the number of years. At what rate is the money in this account growing when 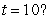
A) $18.12 per year
B) $69.63 per year
C) $1812.38 per year
D) $965.26 per year
E) $126.87 per year

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
13
Find the derivative of the function. 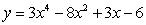
A)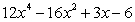
B)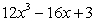
C)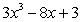
D)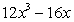
E)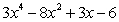
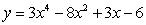
A)
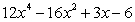
B)
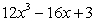
C)
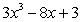
D)
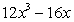
E)
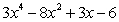

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
14
Find the derivative of the function. 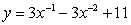
A)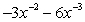
B)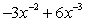
C)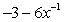
D)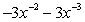
E)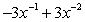
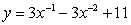
A)
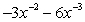
B)
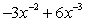
C)
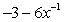
D)
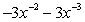
E)
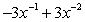

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
15
For the function in this problem, find the derivative, by using the definition. 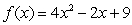
A)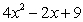
B)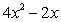
C)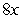
D)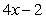
E)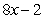
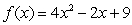
A)
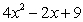
B)
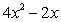
C)
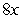
D)
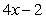
E)
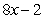

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
16
The managers of a company have modeled some cost data and found that if they produce x storm windows each hour, the cost (in dollars) to produce one window is given by the function 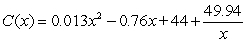 , for
, for 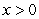 . The company sells its storm windows for $190 each. Assuming that every window made will be sold, give a formula for the profit made from the sale of one storm window when the company is producing x windows each hour.
. The company sells its storm windows for $190 each. Assuming that every window made will be sold, give a formula for the profit made from the sale of one storm window when the company is producing x windows each hour.
A)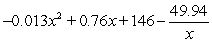
B)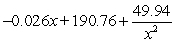
C)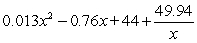
D)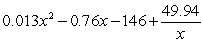
E)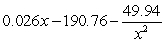
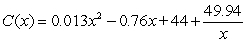 , for
, for 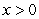 . The company sells its storm windows for $190 each. Assuming that every window made will be sold, give a formula for the profit made from the sale of one storm window when the company is producing x windows each hour.
. The company sells its storm windows for $190 each. Assuming that every window made will be sold, give a formula for the profit made from the sale of one storm window when the company is producing x windows each hour.A)
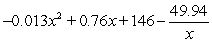
B)
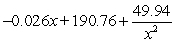
C)
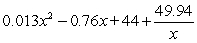
D)
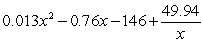
E)
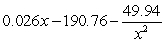

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
17
For the function given, find 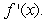
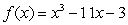
A)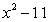
B)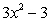
C)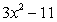
D)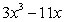
E)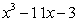
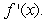
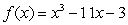
A)
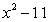
B)
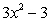
C)
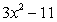
D)
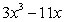
E)
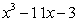

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
18
Calculate the derivative of the function with the appropriate formula. 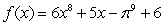
A)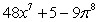
B)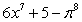
C)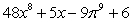
D)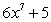
E)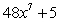
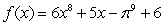
A)
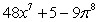
B)
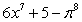
C)
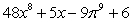
D)
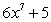
E)
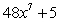

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
19
Find the derivative of 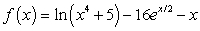 .
.
A)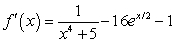
B)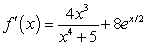
C)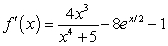
D)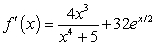
E)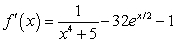
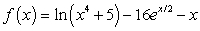 .
.A)
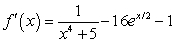
B)
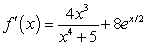
C)
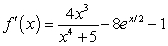
D)
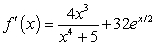
E)
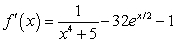

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
20
Differentiate the given function. 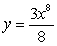
A)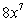
B)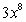
C)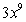
D)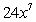
E)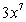
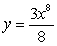
A)
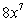
B)
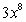
C)
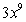
D)
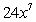
E)
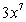

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose the managers of a dairy company have modeled weekly production costs as 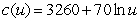 dollars for u units of dairy products. Weekly shipping cost for u units is given by
dollars for u units of dairy products. Weekly shipping cost for u units is given by 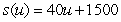 dollars
dollars
Calculate the total cost to produce and ship 4000 units in 1 week. Round to the nearest cent.
A)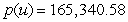
B)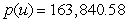
C)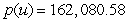
D)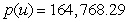
E)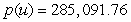
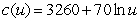 dollars for u units of dairy products. Weekly shipping cost for u units is given by
dollars for u units of dairy products. Weekly shipping cost for u units is given by 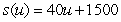 dollars
dollarsCalculate the total cost to produce and ship 4000 units in 1 week. Round to the nearest cent.
A)
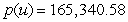
B)
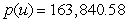
C)
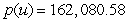
D)
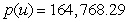
E)
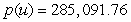

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate 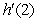 where
where 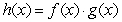 given
given 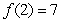 ,
, 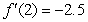 ,
, 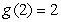 ,
, 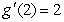 .
.
A) -13.5
B) -10
C) 9
D) 19
E) -19
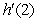 where
where 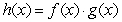 given
given 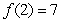 ,
, 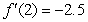 ,
, 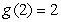 ,
, 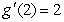 .
.A) -13.5
B) -10
C) 9
D) 19
E) -19

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
23
For the given pair of functions, write the composite function and its derivative in terms of one input variable. 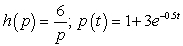
A)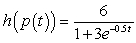 ;
; 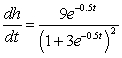
B)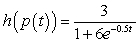 ;
; 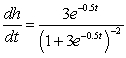
C)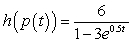 ;
; 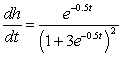
D)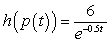 ;
; 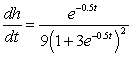
E)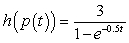 ;
; 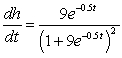
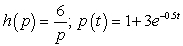
A)
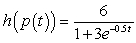 ;
; 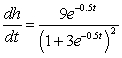
B)
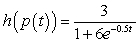 ;
; 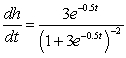
C)
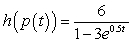 ;
; 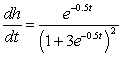
D)
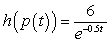 ;
; 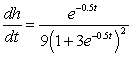
E)
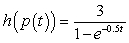 ;
; 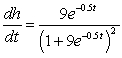

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
24
Using the product rule write the rate-of-change function. 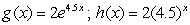
A)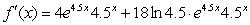
B)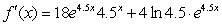
C)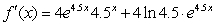
D)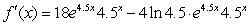
E)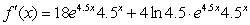
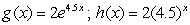
A)
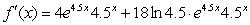
B)
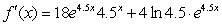
C)
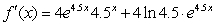
D)
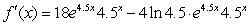
E)
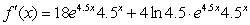

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
25
For the given pair of functions, write the composite function and its derivative in terms of one input variable. 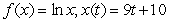
A)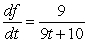
B)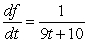
C)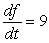
D)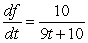
E)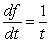
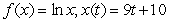
A)
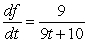
B)
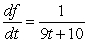
C)
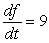
D)
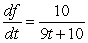
E)
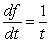

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
26
Differentiate the given function. 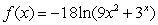
A)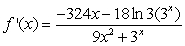
B)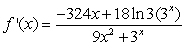
C)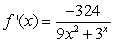
D)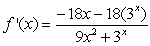
E)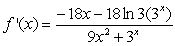
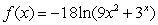
A)
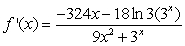
B)
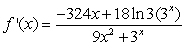
C)
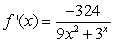
D)
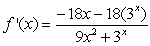
E)
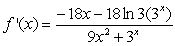

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
27
Find the derivative of 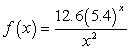 .
.
A)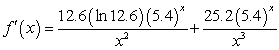
B)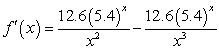
C)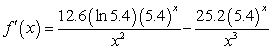
D)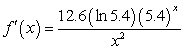
E)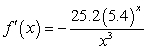
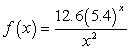 .
.A)
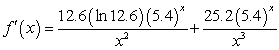
B)
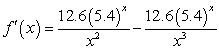
C)
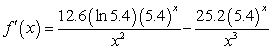
D)
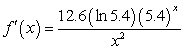
E)
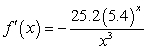

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
28
Using the product rule write the rate-of-change function. 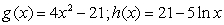
A)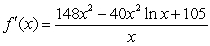
B)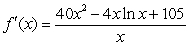
C)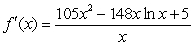
D)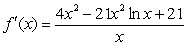
E)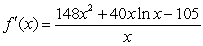
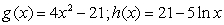
A)
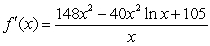
B)
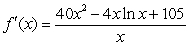
C)
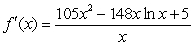
D)
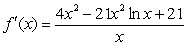
E)
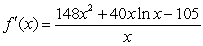

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
29
Differentiate the given function. 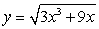
A)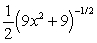
B)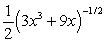
C)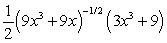
D)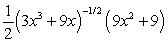
E)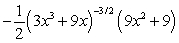
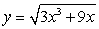
A)
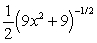
B)
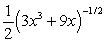
C)
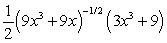
D)
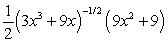
E)
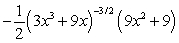

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose the percentage of children living with their grandparents between 1970 and 2000 can be modeled by the equation 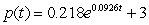 percent, t years after 1970. How rapidly on average did the percentage of children living with their grandparents grow between 1974 and 1993?
percent, t years after 1970. How rapidly on average did the percentage of children living with their grandparents grow between 1974 and 1993?
A) 24.01 % per year
B) 14.06 % per year
C) 16.98 % per year
D) 9.95 % per year
E) 2.92 % per year
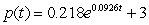 percent, t years after 1970. How rapidly on average did the percentage of children living with their grandparents grow between 1974 and 1993?
percent, t years after 1970. How rapidly on average did the percentage of children living with their grandparents grow between 1974 and 1993?A) 24.01 % per year
B) 14.06 % per year
C) 16.98 % per year
D) 9.95 % per year
E) 2.92 % per year

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
31
Find the derivative of 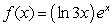 .
.
A)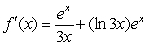
B)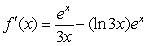
C)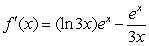
D)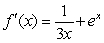
E)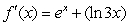
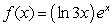 .
.A)
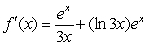
B)
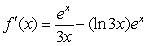
C)
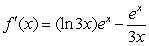
D)
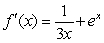
E)
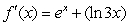

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
32
Find the derivative of 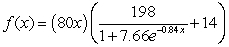 .
.
A)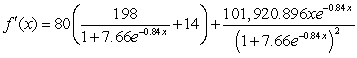
B)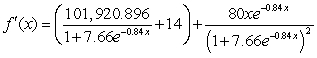
C)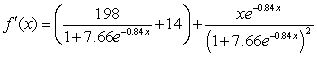
D)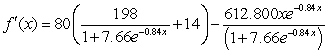
E)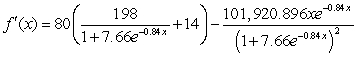
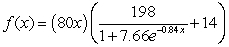 .
.A)
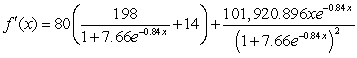
B)
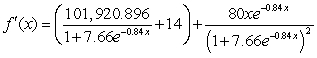
C)
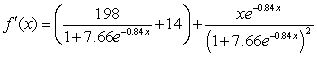
D)
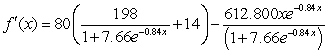
E)
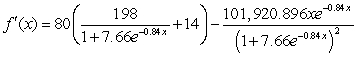

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
33
The GDP of a certain country is $617 billion and is increasing by $22 thousand per person. The population of that country is 76 million and is increasing by 0.9 million people per year. How quickly is the GDP increasing?
A) 19.8 billion per year
B) 25.2 billion per year
C) 68.4 billion per year
D) 138.8 billion per year
E) 555.3 billion per year
A) 19.8 billion per year
B) 25.2 billion per year
C) 68.4 billion per year
D) 138.8 billion per year
E) 555.3 billion per year

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
34
For the given pair of functions, write the composite function and its derivative in terms of one input variable. 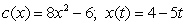
A)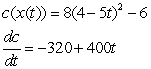
B)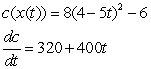
C)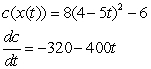
D)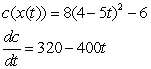
E)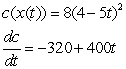
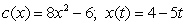
A)
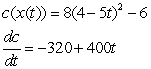
B)
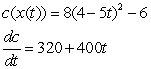
C)
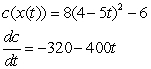
D)
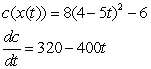
E)
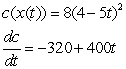

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
35
Differentiate the given function. 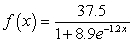
A)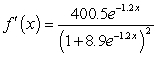
B)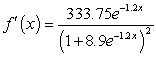
C)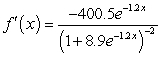
D)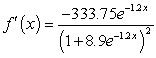
E)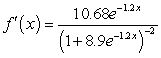
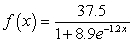
A)
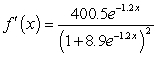
B)
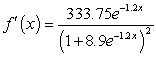
C)
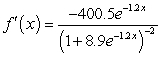
D)
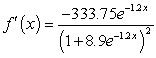
E)
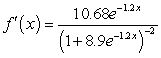

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
36
When t million dollars is invested in technology for a manufacturing plant, the plant needs w(t) workers to maximize production. Labor costs are L(w) million dollars when w workers are employed. When $5 million is invested in technology, 2400 workers are needed to maximize production, and labor needs are increasing by 200 workers per million dollars. It costs $32 million to employ 2400 workers. At 2400 workers, labor costs are increasing by approximately $0.024 per worker. Evaluate w(t) when $5 million is invested in technology, and write a sentence interpreting the value.
A)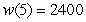 workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2400 workers to minimize production.
workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2400 workers to minimize production.
B)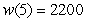 workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2200 workers to maximize production.
workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2200 workers to maximize production.
C)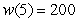 workers When $5 billion is invested in technology for a manufacturing plant, labor needs are increasing by 200 workers per million dollars.
workers When $5 billion is invested in technology for a manufacturing plant, labor needs are increasing by 200 workers per million dollars.
D)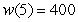 workers When $5 billion is invested in technology for a manufacturing plant, labor needs are decreasing by 400 workers per million dollars.
workers When $5 billion is invested in technology for a manufacturing plant, labor needs are decreasing by 400 workers per million dollars.
E)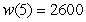 workers When $5 billion is invested in technology for a manufacturing plant, the plant needs 2600 workers to maximize production.
workers When $5 billion is invested in technology for a manufacturing plant, the plant needs 2600 workers to maximize production.
A)
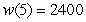 workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2400 workers to minimize production.
workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2400 workers to minimize production.B)
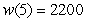 workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2200 workers to maximize production.
workers When $5 million is invested in technology for a manufacturing plant, the plant needs 2200 workers to maximize production.C)
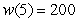 workers When $5 billion is invested in technology for a manufacturing plant, labor needs are increasing by 200 workers per million dollars.
workers When $5 billion is invested in technology for a manufacturing plant, labor needs are increasing by 200 workers per million dollars.D)
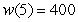 workers When $5 billion is invested in technology for a manufacturing plant, labor needs are decreasing by 400 workers per million dollars.
workers When $5 billion is invested in technology for a manufacturing plant, labor needs are decreasing by 400 workers per million dollars.E)
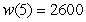 workers When $5 billion is invested in technology for a manufacturing plant, the plant needs 2600 workers to maximize production.
workers When $5 billion is invested in technology for a manufacturing plant, the plant needs 2600 workers to maximize production.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
37
For each of the composite functions, identify an inside function and an outside function and write the derivative with respect to x of the composite function. 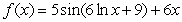
A)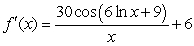
B)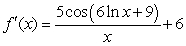
C)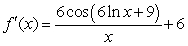
D)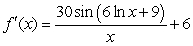
E)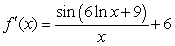
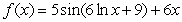
A)
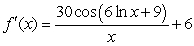
B)
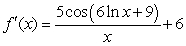
C)
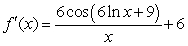
D)
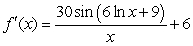
E)
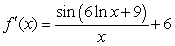

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
38
Find the derivative of 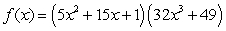 .
.
A)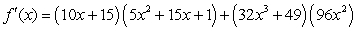
B)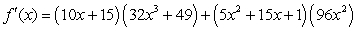
C)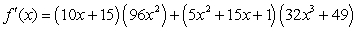
D)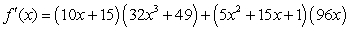
E)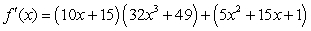
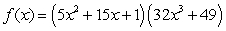 .
.A)
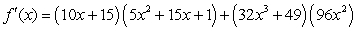
B)
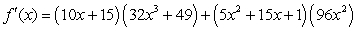
C)
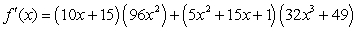
D)
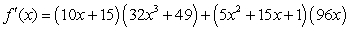
E)
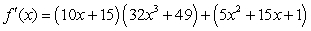

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
39
The revenue from the sale of x units of a commodity is r(x) Canadian dollars, and u(r) U.S. dollars is the equivalent value of r Canadian dollars. On September 8, 2009, $1 Canadian was worth $1.0764 U.S., and the rate of change of the U.S. dollar value was $0.925 U.S. per Canadian dollar. On the same day, sales were 470 units, producing revenue of $10,000 Canadian, and revenue was increasing by $4.2 Canadian per unit. Evaluate 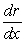 of the given expression on September 8, 2009, and write a sentence interpreting the value.
of the given expression on September 8, 2009, and write a sentence interpreting the value.
A)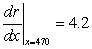 Canadian dollars per unit On September 8, 2009, revenue was increasing by 4.2 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was increasing by 4.2 Canadian dollars per unit.
B)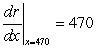 Canadian dollars per unit On September 8, 2009, revenue was increasing by 470 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was increasing by 470 Canadian dollars per unit.
C)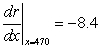 Canadian dollars per unit On September 8, 2009, revenue was decreasing by 8.4 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was decreasing by 8.4 Canadian dollars per unit.
D)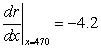 Canadian dollars per unit On September 8, 2009, revenue was decreasing by 4.2 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was decreasing by 4.2 Canadian dollars per unit.
E)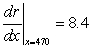 Canadian dollars per unit On September 8, 2009, revenue was increasing by 8.4 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was increasing by 8.4 Canadian dollars per unit.
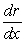 of the given expression on September 8, 2009, and write a sentence interpreting the value.
of the given expression on September 8, 2009, and write a sentence interpreting the value.A)
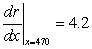 Canadian dollars per unit On September 8, 2009, revenue was increasing by 4.2 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was increasing by 4.2 Canadian dollars per unit.B)
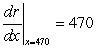 Canadian dollars per unit On September 8, 2009, revenue was increasing by 470 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was increasing by 470 Canadian dollars per unit.C)
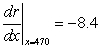 Canadian dollars per unit On September 8, 2009, revenue was decreasing by 8.4 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was decreasing by 8.4 Canadian dollars per unit.D)
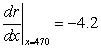 Canadian dollars per unit On September 8, 2009, revenue was decreasing by 4.2 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was decreasing by 4.2 Canadian dollars per unit.E)
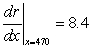 Canadian dollars per unit On September 8, 2009, revenue was increasing by 8.4 Canadian dollars per unit.
Canadian dollars per unit On September 8, 2009, revenue was increasing by 8.4 Canadian dollars per unit.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
40
The population (in millions) of the United States between 1970 and 2010 can be modeled as 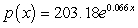 million people where x is the number of decades after 1970.
million people where x is the number of decades after 1970.
The percentage of people in the United States who live in the Midwest between 1970 and 2010 can be modeled as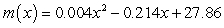 percent
percent
Where x is the number of decades since 1970.
Write an expression for the number of people who live in the Midwest x decades after 1970.
A)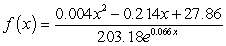 million people
million people
B)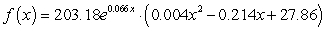 million people
million people
C)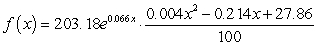 million people
million people
D)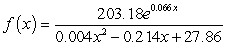 million people
million people
E)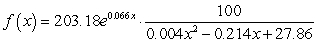 million people
million people
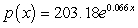 million people where x is the number of decades after 1970.
million people where x is the number of decades after 1970.The percentage of people in the United States who live in the Midwest between 1970 and 2010 can be modeled as
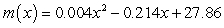 percent
percentWhere x is the number of decades since 1970.
Write an expression for the number of people who live in the Midwest x decades after 1970.
A)
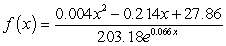 million people
million peopleB)
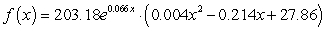 million people
million peopleC)
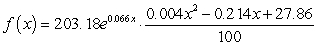 million people
million peopleD)
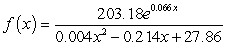 million people
million peopleE)
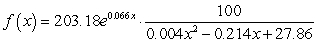 million people
million people
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
41
The profit from the supply of a certain commodity is modeled as 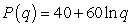 thousand dollars where q is the number of million units produced. How rapidly are profit and average profit changing when 10 million units are produced?
thousand dollars where q is the number of million units produced. How rapidly are profit and average profit changing when 10 million units are produced?
A) $4 thousand per million units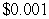 per million units
per million units
B) $60 thousand per million units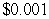 per million units
per million units
C) $40 thousand per million units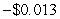 per million units
per million units
D) $40 thousand per million units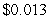 per million units
per million units
E) $6 thousand per million units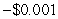 per million units
per million units
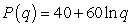 thousand dollars where q is the number of million units produced. How rapidly are profit and average profit changing when 10 million units are produced?
thousand dollars where q is the number of million units produced. How rapidly are profit and average profit changing when 10 million units are produced?A) $4 thousand per million units
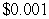 per million units
per million unitsB) $60 thousand per million units
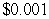 per million units
per million unitsC) $40 thousand per million units
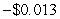 per million units
per million unitsD) $40 thousand per million units
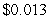 per million units
per million unitsE) $6 thousand per million units
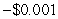 per million units
per million units
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
42
Use L'Hôpital's Rule to find the limit. 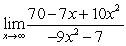
A)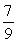
B)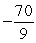
C)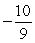
D)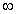
E) Limit does not exist.
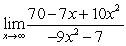
A)
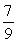
B)
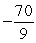
C)
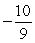
D)
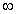
E) Limit does not exist.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate the limit 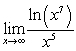 using L'Hôpital's Rule, if necessary.
using L'Hôpital's Rule, if necessary.
A)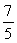

B)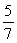
C) 0
D)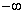
E)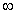
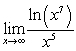 using L'Hôpital's Rule, if necessary.
using L'Hôpital's Rule, if necessary.A)
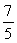

B)
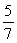
C) 0
D)
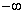
E)
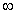

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
44
The number of private donations received by nongovernment disaster relief organizations can be modeled as 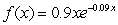 thousand donations where x is the number of hours since a major disaster has struck. At what time is the rate of change of donations zero?
thousand donations where x is the number of hours since a major disaster has struck. At what time is the rate of change of donations zero?
Round to the nearest thousandth.
A) 12.346 hours
B) 0.111 hours
C) 1.111 hours
D) 0.992 hours
E) 11.111 hours
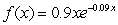 thousand donations where x is the number of hours since a major disaster has struck. At what time is the rate of change of donations zero?
thousand donations where x is the number of hours since a major disaster has struck. At what time is the rate of change of donations zero?Round to the nearest thousandth.
A) 12.346 hours
B) 0.111 hours
C) 1.111 hours
D) 0.992 hours
E) 11.111 hours

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
45
Use L'Hôpital's Rule to find the limit. 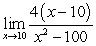
A)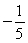
B) 0
C)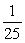
D)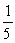
E) Limit does not exist.
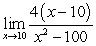
A)
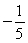
B) 0
C)
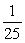
D)
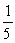
E) Limit does not exist.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate the limit 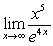 using L'Hôpital's Rule, if necessary.
using L'Hôpital's Rule, if necessary.
A)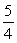
B)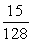
C) 1
D) 0
E) Limit does not exist.
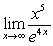 using L'Hôpital's Rule, if necessary.
using L'Hôpital's Rule, if necessary.A)
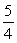
B)
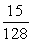
C) 1
D) 0
E) Limit does not exist.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
47
Find 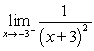 .
.
A) -3
B)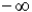
C) 0
D) 3
E) inf
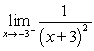 .
.A) -3
B)
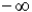
C) 0
D) 3
E) inf

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
48
Determine the following limit. 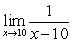
A) 0
B) Does not exist
C) 10
D) -10
E) -20
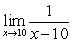
A) 0
B) Does not exist
C) 10
D) -10
E) -20

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck


