Exam 3: Determining Change: Derivatives
Exam 1: Ingredients of Change: Functions an Limits50 Questions
Exam 2: Describing Change: Rates47 Questions
Exam 3: Determining Change: Derivatives48 Questions
Exam 4: Analyzing Change: Applications of Derivatives50 Questions
Exam 5: Accumulating Change: Limits of Sums and the Definite Integral50 Questions
Exam 6: Analyzing Accumulated Change: Integrals in Action51 Questions
Exam 7: Ingredients of Multivariable Change: Models, Graphs, Rates46 Questions
Exam 8: Analyzing Multivariable Change: Optimization50 Questions
Select questions type
Evaluate the limit 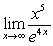 using L'Hôpital's Rule, if necessary.
using L'Hôpital's Rule, if necessary.
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
D
The graph below gives membership in an organization during its first year. Estimate the instantaneous rate of change in membership in September. 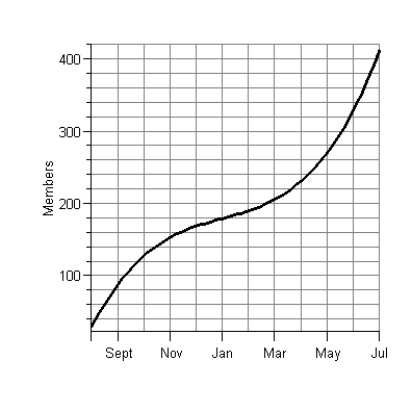
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
A
Suppose the managers of a dairy company have modeled weekly production costs as 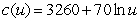 dollars for u units of dairy products. Weekly shipping cost for u units is given by
dollars for u units of dairy products. Weekly shipping cost for u units is given by 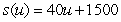 dollars
Calculate the total cost to produce and ship 4000 units in 1 week. Round to the nearest cent.
dollars
Calculate the total cost to produce and ship 4000 units in 1 week. Round to the nearest cent.
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
A
For the function in this problem, find the derivative, by using the definition. 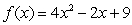
(Multiple Choice)
4.8/5  (38)
(38)
The GDP of a certain country is $617 billion and is increasing by $22 thousand per person. The population of that country is 76 million and is increasing by 0.9 million people per year. How quickly is the GDP increasing?
(Multiple Choice)
4.9/5  (36)
(36)
For the given pair of functions, write the composite function and its derivative in terms of one input variable. 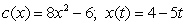
(Multiple Choice)
4.9/5  (32)
(32)
The future value that accrues when $900 is invested at 7%, compounded continuously, is 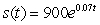 , where t is the number of years. At what rate is the money in this account growing when
, where t is the number of years. At what rate is the money in this account growing when 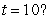
(Multiple Choice)
4.9/5  (34)
(34)
When t million dollars is invested in technology for a manufacturing plant, the plant needs w(t) workers to maximize production. Labor costs are L(w) million dollars when w workers are employed. When $5 million is invested in technology, 2400 workers are needed to maximize production, and labor needs are increasing by 200 workers per million dollars. It costs $32 million to employ 2400 workers. At 2400 workers, labor costs are increasing by approximately $0.024 per worker. Evaluate w(t) when $5 million is invested in technology, and write a sentence interpreting the value.
(Multiple Choice)
4.9/5  (30)
(30)
The profit from the supply of a certain commodity is modeled as 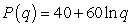 thousand dollars where q is the number of million units produced. How rapidly are profit and average profit changing when 10 million units are produced?
thousand dollars where q is the number of million units produced. How rapidly are profit and average profit changing when 10 million units are produced?
(Multiple Choice)
5.0/5  (27)
(27)
The population (in millions) of the United States between 1970 and 2010 can be modeled as 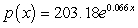 million people where x is the number of decades after 1970.
The percentage of people in the United States who live in the Midwest between 1970 and 2010 can be modeled as
million people where x is the number of decades after 1970.
The percentage of people in the United States who live in the Midwest between 1970 and 2010 can be modeled as 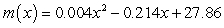 percent
Where x is the number of decades since 1970.
Write an expression for the number of people who live in the Midwest x decades after 1970.
percent
Where x is the number of decades since 1970.
Write an expression for the number of people who live in the Midwest x decades after 1970.
(Multiple Choice)
4.8/5  (32)
(32)
The revenue from the sale of x units of a commodity is r(x) Canadian dollars, and u(r) U.S. dollars is the equivalent value of r Canadian dollars. On September 8, 2009, $1 Canadian was worth $1.0764 U.S., and the rate of change of the U.S. dollar value was $0.925 U.S. per Canadian dollar. On the same day, sales were 470 units, producing revenue of $10,000 Canadian, and revenue was increasing by $4.2 Canadian per unit. Evaluate 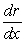 of the given expression on September 8, 2009, and write a sentence interpreting the value.
of the given expression on September 8, 2009, and write a sentence interpreting the value.
(Multiple Choice)
4.9/5  (45)
(45)
Showing 1 - 20 of 48
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)