Deck 17: Second Order Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 17: Second Order Differential Equations
1
A 0.15 kg mass hangs on a spring with a 2 N m-1 force constant and its motion is damped proportional to its velocity with proportionality constant 0.4 kg s-1. If the system is subjected to an external variable-frequency vibration described as 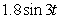 newtons, what will be the amplitude of the steady-state oscillation?
newtons, what will be the amplitude of the steady-state oscillation?
A) 1.32 m
B) 1.74 m
C) 0.53 m
D) 0.00 m
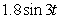 newtons, what will be the amplitude of the steady-state oscillation?
newtons, what will be the amplitude of the steady-state oscillation?A) 1.32 m
B) 1.74 m
C) 0.53 m
D) 0.00 m
1.32 m
2
Solve the initial value problem. 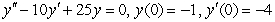
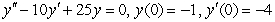
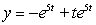
3
Solve the initial value problem 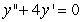 ,
, 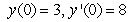 .
.
A)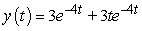
B)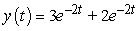
C)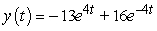
D)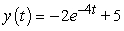
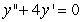 ,
, 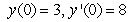 .
.A)
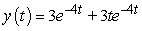
B)
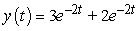
C)
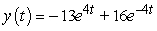
D)
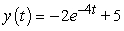
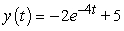
4
Find the general solution of the differential equation. 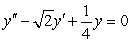
A)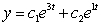
B)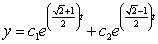
C)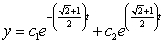
D)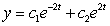
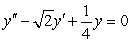
A)
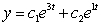
B)
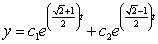
C)
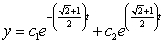
D)
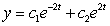

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
Find the general solution of the equation 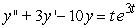 .
.
A)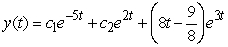
B)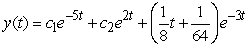
C)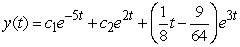
D)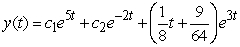
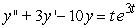 .
.A)
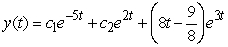
B)
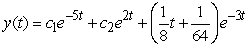
C)
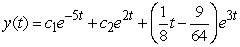
D)
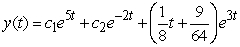

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
Identify the general solution of the the differential equation 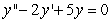 .
.
A)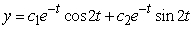
B)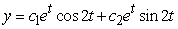
C)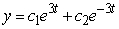
D)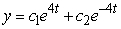
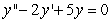 .
.A)
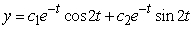
B)
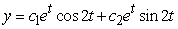
C)
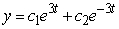
D)
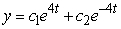

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the initial value problem 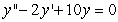 ,
, 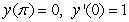 .
.
A)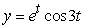
B)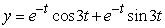
C)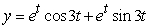
D)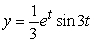
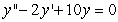 ,
, 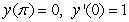 .
.A)
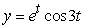
B)
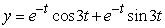
C)
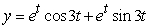
D)
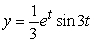

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
Identify the general solution of the the differential equation 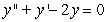 .
.
A)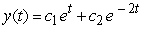
B)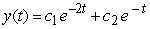
C)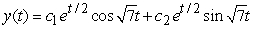
D)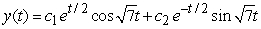
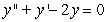 .
.A)
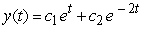
B)
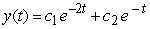
C)
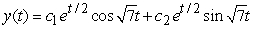
D)
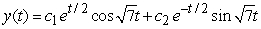

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
Identify the form of a particular solution to the equation 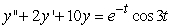 .
.
A)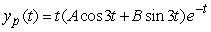
B)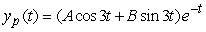
C)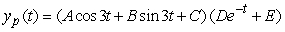
D)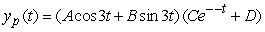
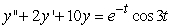 .
.A)
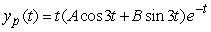
B)
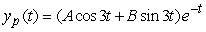
C)
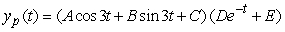
D)
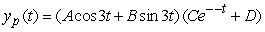

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
A 2.0 kg mass hangs on a spring with a 0.5 newton/meter force constant and its motion is not damped. If the system is subjected to an external variable-frequency vibration described as 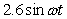 newtons, at what frequency,
newtons, at what frequency, 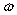 , will the external vibration and the spring system be in resonance?
, will the external vibration and the spring system be in resonance?
A) 0.25 s-1
B) 0.50 s-1
C) 4.00 s-1
D) 2.00 s-1
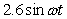 newtons, at what frequency,
newtons, at what frequency, 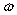 , will the external vibration and the spring system be in resonance?
, will the external vibration and the spring system be in resonance?A) 0.25 s-1
B) 0.50 s-1
C) 4.00 s-1
D) 2.00 s-1

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
Find the general solution of 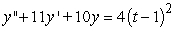 , given the particular solution
, given the particular solution 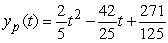 .
.
A)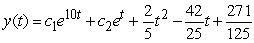
B)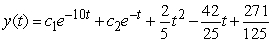
C)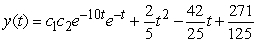
D)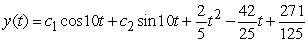
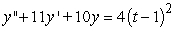 , given the particular solution
, given the particular solution 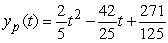 .
.A)
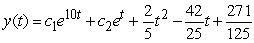
B)
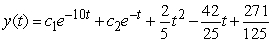
C)
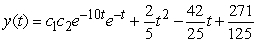
D)
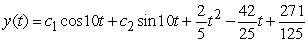

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
Determine the form of a particular solution of the equation. 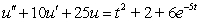
A)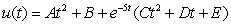
B)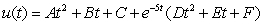
C)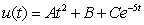
D)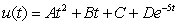
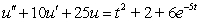
A)
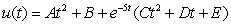
B)
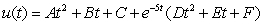
C)
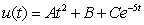
D)
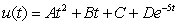

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
A certain spring is at rest when stretched 0.098 m by a 2.0 kg mass. Which function describes the motion of the mass if it is pulled down 0.25 m and released without imparting any initial velocity at time t = 0? Other helpful information: the motion is not damped; use 9.8 m s-2 as the acceleration due to gravity; and consider the zero position to be the rest position of the spring with the mass attached, and downward motion defines the positive x direction.
A)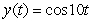
B)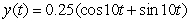
C)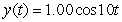
D)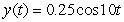
A)
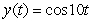
B)
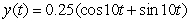
C)
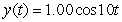
D)
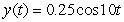

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
Identify the general solution of the the differential equation 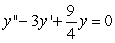 .
.
A)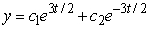
B)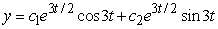
C)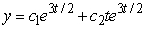
D)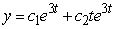
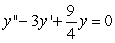 .
.A)
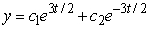
B)
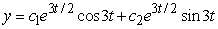
C)
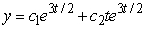
D)
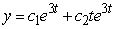

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
Find the general solution of 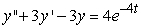 , given the particular solution
, given the particular solution 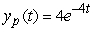 .
.
A)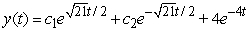
B)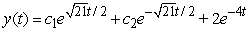
C)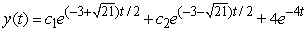
D)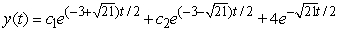
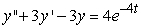 , given the particular solution
, given the particular solution 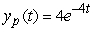 .
.A)
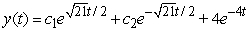
B)
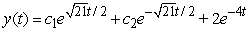
C)
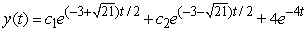
D)
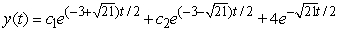

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the initial value problem 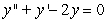 ,
, 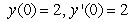 .
.
A)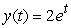
B)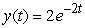
C)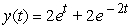
D)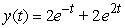
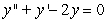 ,
, 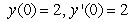 .
.A)
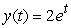
B)
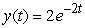
C)
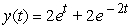
D)
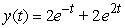

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
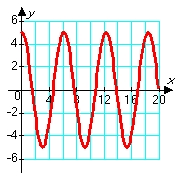
Consider solutions to the second order differential equation 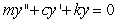 in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?
in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?
A)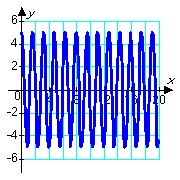
B)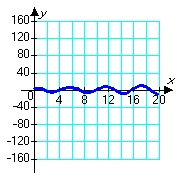
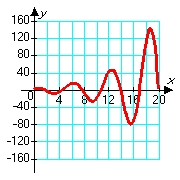
C)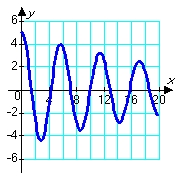
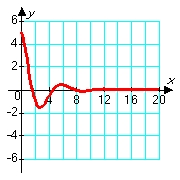
D)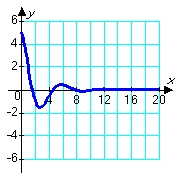
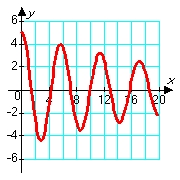
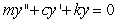 in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?
in which m, c, and k are positive constants. Which of the following pairs of graphs might correspond to the sets of constants m = 1.00, c = 0.80, and k = 1.20 (blue graph), and m = 1.00, c = 0.08, and k = 1.20 (red graph) ?A)


B)


C)


D)



Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
For 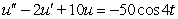 find the steady-state solution and identify its amplitude and phase shift.
find the steady-state solution and identify its amplitude and phase shift.
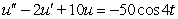 find the steady-state solution and identify its amplitude and phase shift.
find the steady-state solution and identify its amplitude and phase shift.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
A spring is stretched 2 cm by a 1-kg mass. The mass is set in motion from its equilibrium position with an upward velocity of 4 m/s. The damping constant equals 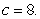 Find an equation for the position of the mass at any time t.
Find an equation for the position of the mass at any time t.
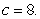 Find an equation for the position of the mass at any time t.
Find an equation for the position of the mass at any time t.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
Identify the form of a particular solution to the equation 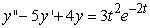 .
.
A)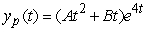
B)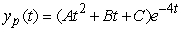
C)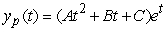
D)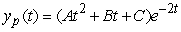
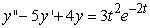 .
.A)
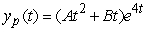
B)
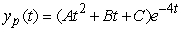
C)
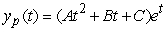
D)
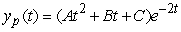

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
A series circuit has a 0.1 henry inductor, a 490 ohm resistor, and a 0.000003 farad capacitor. There is an initial charge of 0.000009 coulombs, there is no initial current, and there is an applied voltage which is described as 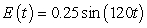 . Identify the steady-state solution to the differential equation.
. Identify the steady-state solution to the differential equation.
A)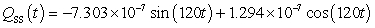
B)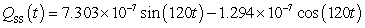
C)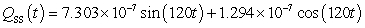
D)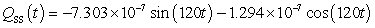
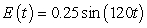 . Identify the steady-state solution to the differential equation.
. Identify the steady-state solution to the differential equation.A)
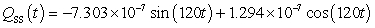
B)
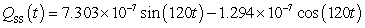
C)
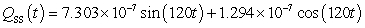
D)
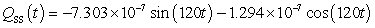

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
A pendulum has length 0.22 meter. A bob is released from rest from a starting angle ![<strong>A pendulum has length 0.22 meter. A bob is released from rest from a starting angle . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s<sup>-2</sup>.]</strong> A) amplitude: 0.2 m; period: 0.941 rad B) amplitude: 0.2 m; period: 0.471 rad C) amplitude: 0.4 m; period: 0.471 rad D) amplitude: 0.4 m; period: 0.941 rad](https://storage.examlex.com/TB5869/11eaa88b_928a_c62b_a696_939147aa6696_TB5869_11.jpg) . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]
. Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]
A) amplitude: 0.2 m; period: 0.941 rad
B) amplitude: 0.2 m; period: 0.471 rad
C) amplitude: 0.4 m; period: 0.471 rad
D) amplitude: 0.4 m; period: 0.941 rad
![<strong>A pendulum has length 0.22 meter. A bob is released from rest from a starting angle . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s<sup>-2</sup>.]</strong> A) amplitude: 0.2 m; period: 0.941 rad B) amplitude: 0.2 m; period: 0.471 rad C) amplitude: 0.4 m; period: 0.471 rad D) amplitude: 0.4 m; period: 0.941 rad](https://storage.examlex.com/TB5869/11eaa88b_928a_c62b_a696_939147aa6696_TB5869_11.jpg) . Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]
. Find an equation for the position at any time t and find the amplitude and period of the motion. [The acceleration due to gravity is 9.8 m s-2.]A) amplitude: 0.2 m; period: 0.941 rad
B) amplitude: 0.2 m; period: 0.471 rad
C) amplitude: 0.4 m; period: 0.471 rad
D) amplitude: 0.4 m; period: 0.941 rad

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose that the charge in a circuit satisfies the equation 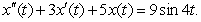 Find the gain of the circuit.
Find the gain of the circuit.
A)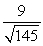
B)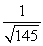
C)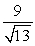
D)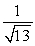
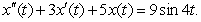 Find the gain of the circuit.
Find the gain of the circuit.A)
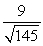
B)
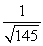
C)
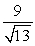
D)
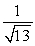

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
A series circuit has a 0.1 henry inductor, a 310 ohm resistor, and a 0.000008 farad capacitor. There is an initial charge of 0.000003 coulombs, there is no initial current, and there is an applied voltage which is described as 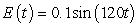 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
A)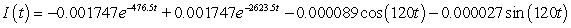
B)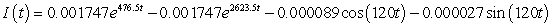
C)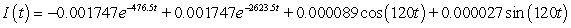
D)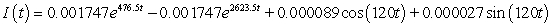
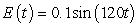 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.A)
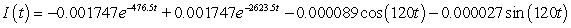
B)
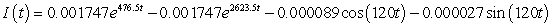
C)
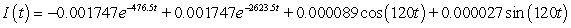
D)
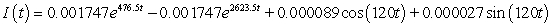

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
A second order differential equaiton can be arranged to the form 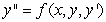 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 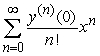 , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation 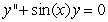 if the initial conditions are
if the initial conditions are 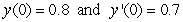 ?
?
A)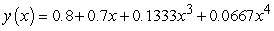
B)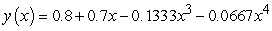
C)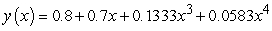
D)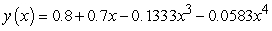
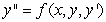 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 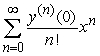 , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What does the fourth-degree Taylor polynomial look like for the solution to the equation 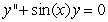 if the initial conditions are
if the initial conditions are 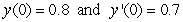 ?
?A)
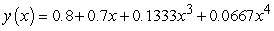
B)
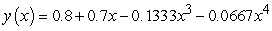
C)
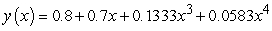
D)
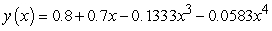

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
A series circuit has a 0.25 henry inductor, a 500 ohm resistor, and a 0.000004 farad capacitor. There is an initial charge of 0.000001 coulombs, there is no initial current, and there is an applied voltage which is described as 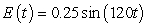 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
A)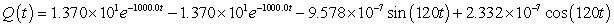
B)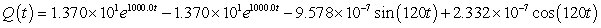
C)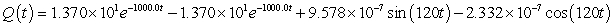
D)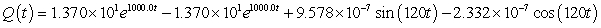
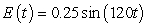 . Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the solution to the differential equation that describes the charge on the capacitor as a function of time.A)
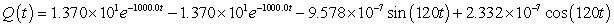
B)
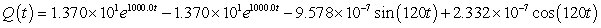
C)
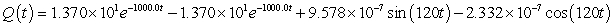
D)
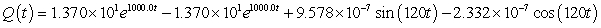

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
Find the recurrence relation for the general power series solution 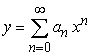 to the second order equation
to the second order equation 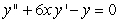 .
.
A)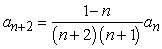
B)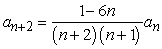
C)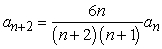
D)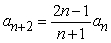
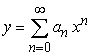 to the second order equation
to the second order equation 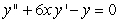 .
.A)
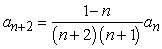
B)
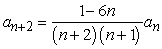
C)
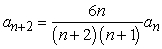
D)
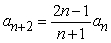

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the initial value problem 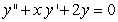 ,
, 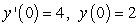 .
.
A)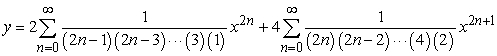
B)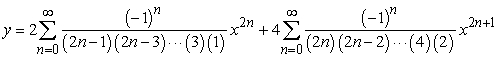
C)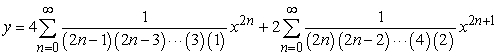
D)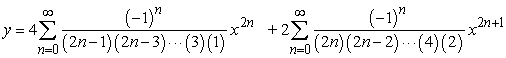
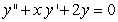 ,
, 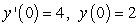 .
.A)
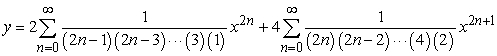
B)
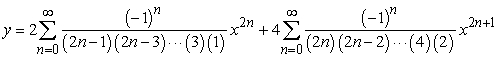
C)
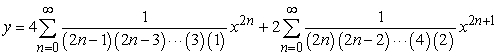
D)
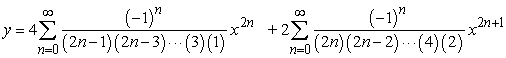

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
A series circuit has an 0.3 henry inductor, a 300 ohm resistor, and a 10-3 farad capacitor. The initial charge on the capacitor is 10-7 coulombs, and there is no initial current nor applied voltage. Identify the function that describes the charge on the capacitor as a function of time.
A)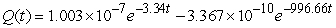
B)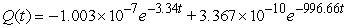
C)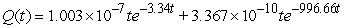
D)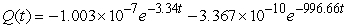
A)
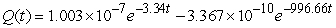
B)
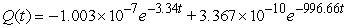
C)
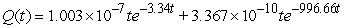
D)
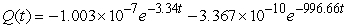

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
Find the recurrence relation for the general power series solution 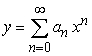 to the second order equation
to the second order equation 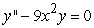 .
.
A)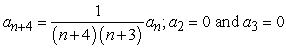
B)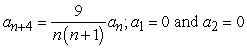
C)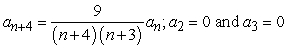
D)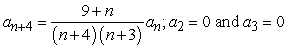
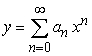 to the second order equation
to the second order equation 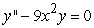 .
.A)
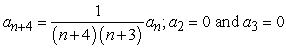
B)
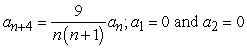
C)
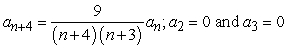
D)
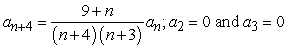

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
Identify the radius of convergence of the power series solutions about x = 0 of 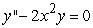 .
.
A)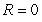
B)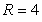
C)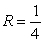
D)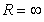
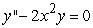 .
.A)
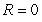
B)
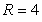
C)
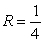
D)
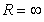

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
A series circuit has a 0.25 henry inductor, a 340 ohm resistor, and a 0.000009 farad capacitor. There is an initial charge of 0.000004 coulombs, there is no initial current, and there is an applied voltage which is described as 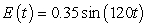 . Identify the amplitude of the steady-state solution.
. Identify the amplitude of the steady-state solution.
A) 0.000003
B) 0.000009
C) 0.35
D) 0.175
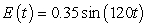 . Identify the amplitude of the steady-state solution.
. Identify the amplitude of the steady-state solution.A) 0.000003
B) 0.000009
C) 0.35
D) 0.175

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
For a pendulum of weight 4 pounds, length 0.60 ft, damping constant ![<strong>For a pendulum of weight 4 pounds, length 0.60 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.400 ft; period: 1.555 rad B) amplitude: 0.200 ft; period: 0.777 rad C) amplitude: 0.092 ft; period: 0.524 rad D) amplitude: 0.184 ft; period: 1.047 rad](https://storage.examlex.com/TB5869/11eaa88b_928b_144c_a696_a3f61fd1345f_TB5869_11.jpg) and forcing function
and forcing function ![<strong>For a pendulum of weight 4 pounds, length 0.60 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.400 ft; period: 1.555 rad B) amplitude: 0.200 ft; period: 0.777 rad C) amplitude: 0.092 ft; period: 0.524 rad D) amplitude: 0.184 ft; period: 1.047 rad](https://storage.examlex.com/TB5869/11eaa88b_928b_3b5d_a696_d503ee1558f8_TB5869_11.jpg) find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]
find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]
A) amplitude: 0.400 ft; period: 1.555 rad
B) amplitude: 0.200 ft; period: 0.777 rad
C) amplitude: 0.092 ft; period: 0.524 rad
D) amplitude: 0.184 ft; period: 1.047 rad
![<strong>For a pendulum of weight 4 pounds, length 0.60 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.400 ft; period: 1.555 rad B) amplitude: 0.200 ft; period: 0.777 rad C) amplitude: 0.092 ft; period: 0.524 rad D) amplitude: 0.184 ft; period: 1.047 rad](https://storage.examlex.com/TB5869/11eaa88b_928b_144c_a696_a3f61fd1345f_TB5869_11.jpg) and forcing function
and forcing function ![<strong>For a pendulum of weight 4 pounds, length 0.60 ft, damping constant and forcing function find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s<sup>-2</sup>.]</strong> A) amplitude: 0.400 ft; period: 1.555 rad B) amplitude: 0.200 ft; period: 0.777 rad C) amplitude: 0.092 ft; period: 0.524 rad D) amplitude: 0.184 ft; period: 1.047 rad](https://storage.examlex.com/TB5869/11eaa88b_928b_3b5d_a696_d503ee1558f8_TB5869_11.jpg) find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]
find the amplitude and period of the steady-state motion. [The acceleration due to gravity is 32 ft s-2.]A) amplitude: 0.400 ft; period: 1.555 rad
B) amplitude: 0.200 ft; period: 0.777 rad
C) amplitude: 0.092 ft; period: 0.524 rad
D) amplitude: 0.184 ft; period: 1.047 rad

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
Identify the radius of convergence of the power series solutions about x = 0 of 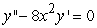 .
.
A) R = 0
B)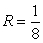
C) R =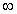
D) R = 8
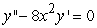 .
.A) R = 0
B)
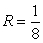
C) R =
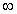
D) R = 8

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the initial value problem 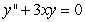 ,
, 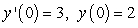 .
.
A)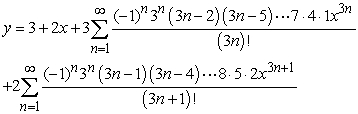
B)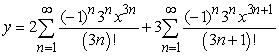
C)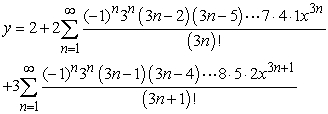
D)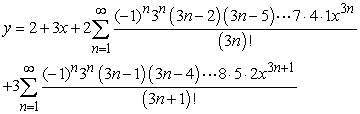
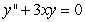 ,
, 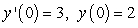 .
.A)
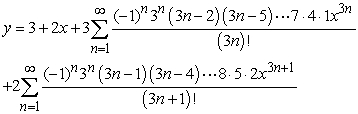
B)
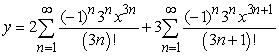
C)
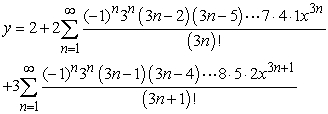
D)
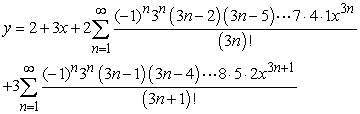

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
Identify the pair of graphs that correspond most closely to the solutions of ![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_6ed3_a696_812bb9a4f027_TB5869_11.jpg) with
with ![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_95e4_a696_4555f46e304f_TB5869_00.jpg) , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]
, respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]
A)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_bcf5_a696_132b5564991f_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_bcf6_a696_91ab1fa9ba09_TB5869_11.jpg)
B)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_e407_a696_f3de91340fd7_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_0b18_a696_797920d700af_TB5869_11.jpg)
C)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_3229_a696_717b4463580f_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_593a_a696_03c872d7920e_TB5869_11.jpg)
D)![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_804b_a696_f9d387f6b46f_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_a75c_a696_f7d1376b4d88_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_6ed3_a696_812bb9a4f027_TB5869_11.jpg) with
with ![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_95e4_a696_4555f46e304f_TB5869_00.jpg) , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]
, respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]A)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_bcf5_a696_132b5564991f_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_bcf6_a696_91ab1fa9ba09_TB5869_11.jpg)
B)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9285_e407_a696_f3de91340fd7_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_0b18_a696_797920d700af_TB5869_11.jpg)
C)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_3229_a696_717b4463580f_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_593a_a696_03c872d7920e_TB5869_11.jpg)
D)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_804b_a696_f9d387f6b46f_TB5869_11.jpg)
![<strong>Identify the pair of graphs that correspond most closely to the solutions of with , respectively. [The function y(t) is plotted on the vertical axes and t is plotted on the horizontal axes.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9286_a75c_a696_f7d1376b4d88_TB5869_11.jpg)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
A series circuit has a 0.15 henry inductor, a 490 ohm resistor, and a 0.000004 farad capacitor. There is an applied voltage which is described as 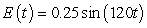 . Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
A)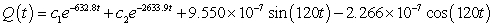
B)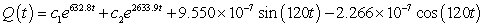
C)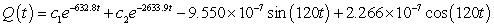
D)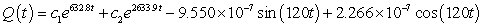
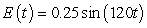 . Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.A)
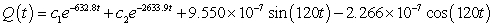
B)
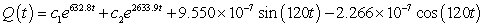
C)
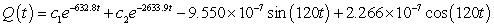
D)
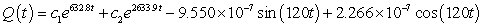

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
A second order differential equation can be arranged to the form 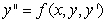 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 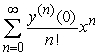 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 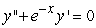 if the initial conditions are
if the initial conditions are 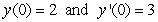 ?
?
A)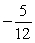
B)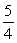
C)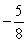
D)
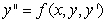 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 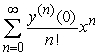 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 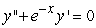 if the initial conditions are
if the initial conditions are 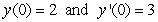 ?
?A)
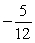
B)
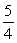
C)
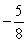
D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck


