Deck 8: Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/127
Play
Full screen (f)
Deck 8: Sampling Distributions
1
The mean of the sampling distribution of the sample proportion 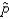 , when the sample size n = 100 and the population proportion p = 0.92, is 92.0.
, when the sample size n = 100 and the population proportion p = 0.92, is 92.0.
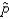 , when the sample size n = 100 and the population proportion p = 0.92, is 92.0.
, when the sample size n = 100 and the population proportion p = 0.92, is 92.0.False
2
Consider an infinite population with a mean of 100 and a standard deviation of 20. A random sample of size 64 is taken from this population. The standard deviation of the sample mean equals 2.50.
True
3
The amount of time it takes to complete a final examination is negatively skewed distribution with a mean of 70 minutes and a standard deviation of 8 minutes. If 64 students were randomly sampled, the probability that the sample mean of the sampled students exceeds 73.5 minutes is approximately 0.
True
4
If all possible samples of size n are drawn from a normal population, the probability distribution of the sample mean 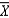 is an exact normal distribution.
is an exact normal distribution.
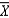 is an exact normal distribution.
is an exact normal distribution.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
5
As the size of the sample is increased, the standard error of 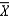 decreases.
decreases.
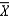 decreases.
decreases.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
6
A sample of size 25 is selected from a population of size 75. The finite population correction needed to find the standard error of 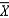 .
.
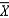 .
.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
7
A sampling distribution is a probability distribution for a statistic, not a parameter.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
8
If the population distribution is skewed, in most cases the sampling distribution of the sample mean can be approximated by the normal distribution if the samples contain at least 30 observations.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
9
If the population distribution is unknown, in most cases the sampling distribution of the mean can be approximated by the normal distribution if the samples contain at least 30 observations.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
10
A sample of size n is selected at random from an infinite population. As n increases, the standard error of the sample mean increases.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
11
If all possible samples of size n are drawn from an infinite population with standard deviation 8, then the standard error of the sample mean equals 1.0 if the sample size is 64.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
12
If the sample size increases, the standard error of the mean also increases.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
13
A sample of size 25 is selected from a population of size 500. The finite population correction is needed to find the standard error of 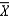 .
.
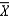 .
.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
14
When a great many simple random samples of size n are drawn from a population that is normally distributed, the sampling distribution of the sample mean is normal regardless of the sample size n.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
15
As the size of the sample is increased, the mean of 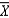 increases.
increases.
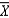 increases.
increases.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
16
The Central Limit Theorem permits us to draw conclusions about a population based on a sample alone, without having any knowledge about the distribution of that population. And this works no matter what the sample size is.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
17
The amount of bleach a machine pours into bottles has a mean of 50 ounces with a standard deviation of 0.25 ounces. Suppose we take a random sample of 36 bottles filled by this machine. The sampling distribution of the sample mean has a standard error of 0.25 ounces.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
18
A sampling distribution is defined as the probability distribution of means from all possible sample sizes that are taken from a given population.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
19
The amount of bleach a machine pours into bottles has a mean of 50 ounces with a standard deviation of 0.25 ounces. We take a random sample of 36 bottles filled by this machine. The sampling distribution of the sample mean has a mean of 50 ounces.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
20
In inferential statistics, the standard error of the sample mean assesses the uncertainty or error of estimation.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
21
The Central Limit Theorem states that, if a random sample of size n is drawn from a population, then the sampling distribution of the sample mean 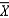 :
:
A) is approximately normal if n < 30.
B) is approximately normal if n > 30.
C) is approximately normal if the underlying population is normal.
D) None of these choices.
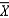 :
:A) is approximately normal if n < 30.
B) is approximately normal if n > 30.
C) is approximately normal if the underlying population is normal.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
22
As a general rule, the normal distribution is used to approximate the sampling distribution of the sample proportion only if the sample size n is greater than or equal to 30.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
23
In general, the binomial probability P(X = x) is approximated by the area under a normal curve between x- .5 and x + .5.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
24
Given an infinite population with a mean of 75 and a standard deviation of 12, the probability that the mean of a sample of 36 observations, taken at random from this population, is less than 78 is:
A) 0.9332
B) 0.5987
C) 1.5000
D) None of these choices.
A) 0.9332
B) 0.5987
C) 1.5000
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
25
Recall the rule of thumb used to indicate when the normal distribution is a good approximation of the sampling distribution for the sample proportion 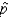 . For the combination n = 50, p = 0.05, the rule is satisfied.
. For the combination n = 50, p = 0.05, the rule is satisfied.
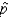 . For the combination n = 50, p = 0.05, the rule is satisfied.
. For the combination n = 50, p = 0.05, the rule is satisfied.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
26
As a general rule in computing the standard error of the sample mean, the finite population correction factor is used only if the:
A) sample size is smaller than 5% of the population size.
B) sample size is greater than 5% of the sample size.
C) sample size is more than half of the population size.
D) None of these choices.
A) sample size is smaller than 5% of the population size.
B) sample size is greater than 5% of the sample size.
C) sample size is more than half of the population size.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
27
Random samples of size 49 are taken from an infinite population whose mean is 300 and standard deviation is 21. The mean and standard error of the sample mean, respectively, are:
A) 300 and 21
B) 300 and 3
C) 300 and 0.43
D) None of these choices.
A) 300 and 21
B) 300 and 3
C) 300 and 0.43
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
28
A sample of size 25 is selected at random from a finite population. If the finite population correction factor is 0.63, then the population size is:
A) 25
B) 66
C) 41
D) None of these choices.
A) 25
B) 66
C) 41
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
29
If a simple random sample of 300 observations is taken from a population whose proportion p = 0.6, then the expected value of the sample proportion 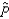 is 0.60.
is 0.60.
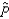 is 0.60.
is 0.60.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
30
The standard error of the sampling distribution of the sample proportion 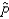 , when the sample size n = 100 and the population proportion p = 0.30, is 0.0021.
, when the sample size n = 100 and the population proportion p = 0.30, is 0.0021.
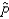 , when the sample size n = 100 and the population proportion p = 0.30, is 0.0021.
, when the sample size n = 100 and the population proportion p = 0.30, is 0.0021.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
31
The standard deviation of the sampling distribution of 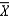 is also called the:
is also called the:
A) central limit theorem.
B) population standard deviation.
C) finite population correction factor.
D) standard error of the sample mean.
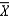 is also called the:
is also called the:A) central limit theorem.
B) population standard deviation.
C) finite population correction factor.
D) standard error of the sample mean.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
32
In an effort to identify the true proportion of college freshman who are under 18 years of age, a random sample of 500 freshmen was taken. Fifty of them were under the age of 18. The value 0.10 is a point estimate of the true proportion of freshman under age 18.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
33
The finite population correction factor should be used:
A) whenever we are sampling from an infinite population.
B) whenever we are sampling from a finite population.
C) whenever the sample size is large compared to the population size.
D) whenever the sample size is small compared to the population size.
A) whenever we are sampling from an infinite population.
B) whenever we are sampling from a finite population.
C) whenever the sample size is large compared to the population size.
D) whenever the sample size is small compared to the population size.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
34
Random samples of size 81 are taken from an infinite population whose mean and standard deviation are 45 and 9, respectively. The mean and standard error of the sampling distribution of the sample mean are:
A) 45 and 9
B) 45/81 and 9/81
C) 45 and 9/ 81
D) 45/ 81 and 9/ 81
A) 45 and 9
B) 45/81 and 9/81
C) 45 and 9/ 81
D) 45/ 81 and 9/ 81

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
35
In general, the binomial probability P(X x) is approximated by the area under the normal curve to the left of x - .5.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
36
Consider an infinite population with a mean of 160 and a standard deviation of 25. A random sample of size 64 is taken from this population. The standard deviation of the sample mean equals:
A) 25
B) 25/64
C) 25/ 64
D) None of these choices.
A) 25
B) 25/64
C) 25/ 64
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
37
A sample of size 40 is taken from an infinite population whose mean and standard deviation are 68 and 12, respectively. The probability that the sample mean is larger than 70 equals
A) P(Z > 70)
B) P(Z > 2)
C) P(Z > 0.17)
D) P(Z > 1.05)
A) P(Z > 70)
B) P(Z > 2)
C) P(Z > 0.17)
D) P(Z > 1.05)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
38
If all possible samples of size n are drawn from an infinite population with a mean of 15 and a standard deviation of 5, then the standard error of the sample mean equals 1.0 for samples of size:
A) 5
B) 15
C) 25
D) None of these choices.
A) 5
B) 15
C) 25
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
39
In general, the binomial probability P(X x) is approximated by the area under the normal curve to the left of x + .5.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
40
An infinite population has a mean of 40 and a standard deviation of 15. A sample of size 100 is taken at random from this population. The standard error of the sample mean equals:
A) 15
B) 15/ 100
C) 15/100
D) None of these choices.
A) 15
B) 15/ 100
C) 15/100
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
41
Given that X is a binomial random variable with very large n, the binomial probability P(X 5) is approximated by the area under a normal curve to the right of
A) 4.5
B) 5.5
C) 4
D) 6
A) 4.5
B) 5.5
C) 4
D) 6

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
42
If all possible samples of size n are drawn from a population, the probability distribution of the sample mean 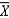 is called the:
is called the:
A) standard error of.
B) expected value of.
C) sampling distribution of.
D) normal distribution.
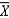 is called the:
is called the:A) standard error of.
B) expected value of.
C) sampling distribution of.
D) normal distribution.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
43
A sample of size n is selected at random from an infinite population. As n increases, which of the following statements is true?
A) The population standard deviation decreases.
B) The standard error of the sample mean decreases.
C) The population standard deviation increases.
D) The standard error of the sample mean increases.
A) The population standard deviation decreases.
B) The standard error of the sample mean decreases.
C) The population standard deviation increases.
D) The standard error of the sample mean increases.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
44
Sampling distributions describe the distributions of:
A) sample statistics.
B) population parameters.
C) both parameters and statistics
D) None of these choices.
A) sample statistics.
B) population parameters.
C) both parameters and statistics
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
45
As a general rule, the normal distribution is used to approximate the sampling distribution of the sample proportion only if:
A) the sample size n is greater than 30.
B) the population proportion p is close to 0.50.
C) the underlying population is normal.
D) np and n(1-p) are both greater than or equal to 5.
A) the sample size n is greater than 30.
B) the population proportion p is close to 0.50.
C) the underlying population is normal.
D) np and n(1-p) are both greater than or equal to 5.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
46
The standard error of the mean:
A) is never larger than the standard deviation of the population.
B) decreases as the sample size increases.
C) measures the variability of the mean from sample to sample.
D) All of these choices are true.
A) is never larger than the standard deviation of the population.
B) decreases as the sample size increases.
C) measures the variability of the mean from sample to sample.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
47
For a sample size of 1, the sampling distribution of the mean is normally distributed:
A) regardless of the shape of the population.
B) only if the population values are larger than 30.
C) only if the population is normally distributed.
D) None of these choices.
A) regardless of the shape of the population.
B) only if the population values are larger than 30.
C) only if the population is normally distributed.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose X has a distribution that is not normal. The Central Limit Theorem is important in this case because:
A) it says the sampling distribution ofis approximately normal for any sample size.
B) it says the sampling distribution ofis approximately normal if n is large enough.
C) it says the sampling distribution ofis exactly normal, for any sample size.
D) None of these choices.
A) it says the sampling distribution ofis approximately normal for any sample size.
B) it says the sampling distribution ofis approximately normal if n is large enough.
C) it says the sampling distribution ofis exactly normal, for any sample size.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
49
If a random sample of size n is drawn from a normal population, then the sampling distribution of the sample mean 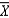 will be:
will be:
A) normal for all values of n.
B) normal only for n > 30.
C) approximately normal for all values of n.
D) approximately normal only for n > 30.
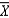 will be:
will be:A) normal for all values of n.
B) normal only for n > 30.
C) approximately normal for all values of n.
D) approximately normal only for n > 30.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
50
The owner of a meat market has an assistant who has determined that the weights of roasts are normally distributed, with a mean of 3.2 pounds and standard deviation of 0.8 pounds. If a sample of 25 roasts yields a mean of 3.6 pounds, what is the Z-score for this sample mean?
A) -2.50
B) 2.50
C)-0.50
D) None of these choices.
A) -2.50
B) 2.50
C)-0.50
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
51
The standard error of the mean for a sample of 100 is 25. In order to cut the standard error of the mean in half (to 12.5) we must:
A) increase the sample size to 200.
B) decrease the sample size to 50.
C) keep the sample size at 100 and change something else.
D) None of these choices.
A) increase the sample size to 200.
B) decrease the sample size to 50.
C) keep the sample size at 100 and change something else.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
52
For sample sizes greater than 30, the sampling distribution of the mean is approximately normally distributed:
A) regardless of the shape of the population.
B) only if the shape of the population is symmetric.
C) only if the population is normally distributed.
D) None of these choices.
A) regardless of the shape of the population.
B) only if the shape of the population is symmetric.
C) only if the population is normally distributed.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
53
Which of the following statements about the sampling distribution of 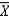 is NOT true?
is NOT true?
A) It is generated by taking all possible samples of size n and computing their sample means.
B) Its mean is equal to the population mean .
C) Its standard deviation is equal to the population standard deviation .
D) All of these choices are true.
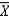 is NOT true?
is NOT true?A) It is generated by taking all possible samples of size n and computing their sample means.
B) Its mean is equal to the population mean .
C) Its standard deviation is equal to the population standard deviation .
D) All of these choices are true.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following is true regarding the sampling distribution of the mean for a large sample size? Assume the population distribution is not normal.
A) It has the same shape, mean and standard deviation as the population.
B) It has the same mean as the population, but a different shape and standard deviation.
C) It the same mean and standard deviation as the population, but a different shape.
D) It has the same shape and mean as the population, but a different standard deviation.
A) It has the same shape, mean and standard deviation as the population.
B) It has the same mean as the population, but a different shape and standard deviation.
C) It the same mean and standard deviation as the population, but a different shape.
D) It has the same shape and mean as the population, but a different standard deviation.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
55
The owner of a fish market has an assistant who has determined that the weights of catfish are normally distributed, with a mean of 3.2 pounds and standard deviation of 0.84 pounds. If a sample of 16 fish is taken, what is the standard error of the mean weight?
A) 0.840
B) 0.053
C) 0.210
D) None of these choices.
A) 0.840
B) 0.053
C) 0.210
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose that 100 items are drawn from a population of manufactured products and the weight, X, of each item is recorded. Prior experience has shown that the weight has a non-normal probability distribution with = 8 ounces and = 3 ounces. Which of the following is true about the sampling of 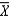 ?
?
A) Its mean is 8 ounces.
B) Its standard error is 0.3 ounces.
C) Its shape is approximately normal.
D) All of these choices are true.
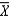 ?
?A) Its mean is 8 ounces.
B) Its standard error is 0.3 ounces.
C) Its shape is approximately normal.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
57
Given that X is a binomial random variable with very large n, the binomial probability P(X = 5) is approximated by the area under a normal curve between
A) 5 and 5
B) 4 and 6
C) 4.5 and 5.5
D) None of these choices.
A) 5 and 5
B) 4 and 6
C) 4.5 and 5.5
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
58
The expected value of the sampling distribution of the sample mean 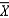 equals the population mean :
equals the population mean :
A) only when the population is normally distributed.
B) only when the sample size is large.
C) only when the population is infinite.
D) for all populations.
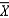 equals the population mean :
equals the population mean :A) only when the population is normally distributed.
B) only when the sample size is large.
C) only when the population is infinite.
D) for all populations.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
59
Given that X is a binomial random variable with very large n, the binomial probability P(X 5) is approximated by the area under a normal curve to the left of
A) 5
B) -5
C) 5.5
D) 4.5
A) 5
B) -5
C) 5.5
D) 4.5

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
60
Which of the following is true about the sampling distribution of the sample mean?
A) Its mean is always equal to
B) Its standard error is always equal to the population standard deviation .
C) Its shape is exactly normal if n is large enough.
D) None of these choices.
A) Its mean is always equal to
B) Its standard error is always equal to the population standard deviation .
C) Its shape is exactly normal if n is large enough.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
61
The standard deviation of 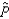 is also called the:
is also called the:
A) standard error of the sample proportion.
B) standard deviation of the population.
C) standard deviation of the binomial.
D) None of these choices.
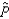 is also called the:
is also called the:A) standard error of the sample proportion.
B) standard deviation of the population.
C) standard deviation of the binomial.
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
62
As the number of throws of a fair die increases, the probability that the sample mean is close to (the number) ____________________ increases.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
63
A sample of size 200 is taken at random from an infinite population. Given that the population proportion is 0.60, the probability that the sample proportion is between 0.58 and 0.62 is:
A) 0.4314
B) 0.0320
C) 0.0200
D) None of these choices.
A) 0.4314
B) 0.0320
C) 0.0200
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
64
A sample of size 200 is taken at random from an infinite population. Given that the population proportion is 0.60, the probability that the sample proportion is less than 0.58 is
A) 0.281
B) 0.719
C) 0.580
D) 0.762
A) 0.281
B) 0.719
C) 0.580
D) 0.762

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
65
The width of the sampling distribution of 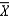 gets ____________________ as the sample size increases.
gets ____________________ as the sample size increases.
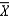 gets ____________________ as the sample size increases.
gets ____________________ as the sample size increases.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
66
The standard error of the sample proportion gets larger as:
A) p approaches 0
B) p approaches 0.50
C) p approaches 1.00
D) None of these choices.
A) p approaches 0
B) p approaches 0.50
C) p approaches 1.00
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose that the probability p of success on any trail of a binomial distribution equals 0.90. Then for which of the following number of trials, n, would the normal distribution provide a good approximation to the binomial distribution?
A) 35
B) 45
C) 55
D) All of these choices are true.
A) 35
B) 45
C) 55
D) All of these choices are true.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
68
Given a binomial distribution with n trials and probability p of a success on any trial, a conventional rule of thumb is that the normal distribution will provide an adequate approximation of the binomial distribution if
A) np 5 and n(1 - p) 5
B) np 5 and np(1 -p) 5
C) np 5 and n(1 - p) 5
D) None of these choices.
A) np 5 and n(1 - p) 5
B) np 5 and np(1 -p) 5
C) np 5 and n(1 - p) 5
D) None of these choices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
69
As n gets larger, the sampling distribution of 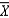 becomes increasingly bell shaped. This phenomenon is due to the ____________________.
becomes increasingly bell shaped. This phenomenon is due to the ____________________.
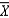 becomes increasingly bell shaped. This phenomenon is due to the ____________________.
becomes increasingly bell shaped. This phenomenon is due to the ____________________.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
70
The accuracy of the approximation of 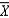 with a normal distribution depends on the probability distribution of the ____________________ and on the sample ____________________.
with a normal distribution depends on the probability distribution of the ____________________ and on the sample ____________________.
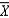 with a normal distribution depends on the probability distribution of the ____________________ and on the sample ____________________.
with a normal distribution depends on the probability distribution of the ____________________ and on the sample ____________________.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
71
If the population is normal, then 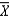 is normally distributed for __________________ values of n.
is normally distributed for __________________ values of n.
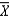 is normally distributed for __________________ values of n.
is normally distributed for __________________ values of n.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
72
A sample of size 200 is taken at random from an infinite population. Given that the population proportion is 0.60, the probability that the sample proportion is greater than 0.58 is:
A) 0.281
B) 0.719
C) 0.580
D) 0.762
A) 0.281
B) 0.719
C) 0.580
D) 0.762

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
73
The estimator of the probability of success in a binomial distribution is: ____________________.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
74
Under certain conditions where n is large enough, you can approximate the ____________________ distribution using the ____________________ distribution.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
75
The finite population correction is not needed if the population size is large relative to the sample size. As a rule of thumb, we will treat any population that is at least ____________________ times larger than the sample size as large.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
76
A sample of 250 observations is selected at random from an infinite population. Given that the population proportion is .25, the standard error of the sampling distribution of the sample proportion is:
A) 0.0274
B) 0.5000
C) 0.0316
D) 0.0548
A) 0.0274
B) 0.5000
C) 0.0316
D) 0.0548

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
77
A randomly selected value of 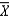 is likely to be ____________________ to(than) the mean of the population than is a randomly selected value of X.
is likely to be ____________________ to(than) the mean of the population than is a randomly selected value of X.
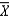 is likely to be ____________________ to(than) the mean of the population than is a randomly selected value of X.
is likely to be ____________________ to(than) the mean of the population than is a randomly selected value of X.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
78
The variance of the sampling distribution of 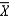 is ____________________ the variance of the population we're sampling from, for any n > 1.
is ____________________ the variance of the population we're sampling from, for any n > 1.
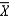 is ____________________ the variance of the population we're sampling from, for any n > 1.
is ____________________ the variance of the population we're sampling from, for any n > 1.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
79
Because the value of the ____________________ varies from sample to sample, we can regard it as a new random variable, created by sampling.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
80
As n gets ____________________, the shape of the sampling distribution of 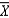 becomes increasingly bell shaped.
becomes increasingly bell shaped.
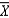 becomes increasingly bell shaped.
becomes increasingly bell shaped.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck


