Deck 5: Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/239
Play
Full screen (f)
Deck 5: Integrals
1
Use the Midpoint Rule with n = 4 to approximate the integral
A)16.25
B)0.505
C)5.4167
D)1.5
E)5.625
F)11.25
G)5.3033
H)2.5
A)16.25
B)0.505
C)5.4167
D)1.5
E)5.625
F)11.25
G)5.3033
H)2.5
5.3033
2
Use the Midpoint Rule with n = 4 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)
3
Use Simpson's Rule with n = 4 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)
4
Estimate 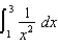 using the Trapezoidal Rule with n = 4. Then use the error bound
using the Trapezoidal Rule with n = 4. Then use the error bound 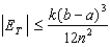 to estimate the accuracy.
to estimate the accuracy.
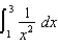 using the Trapezoidal Rule with n = 4. Then use the error bound
using the Trapezoidal Rule with n = 4. Then use the error bound 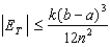 to estimate the accuracy.
to estimate the accuracy.
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
5
Use Simpson's Rule with n = 4 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the integral 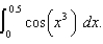 Approximating it by the Midpoint Rule with n equal subintervals, give an estimate for n which guarantees that the error is bounded by
Approximating it by the Midpoint Rule with n equal subintervals, give an estimate for n which guarantees that the error is bounded by 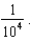
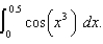 Approximating it by the Midpoint Rule with n equal subintervals, give an estimate for n which guarantees that the error is bounded by
Approximating it by the Midpoint Rule with n equal subintervals, give an estimate for n which guarantees that the error is bounded by 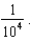

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
7
Use the Trapezoidal Rule with n = 4 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
8
Use the Trapezoidal Rule with n = 4 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
9
Estimate 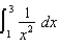 using the Midpoint Rule with n = 4. Then use the error bound
using the Midpoint Rule with n = 4. Then use the error bound 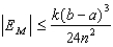 to estimate the accuracy.
to estimate the accuracy.
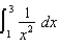 using the Midpoint Rule with n = 4. Then use the error bound
using the Midpoint Rule with n = 4. Then use the error bound 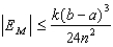 to estimate the accuracy.
to estimate the accuracy.
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
10
Use the Midpoint Rule with 2 equal subdivisions to get an approximation for ln 5.

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
11
Estimate 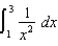 using Simpson's Rule with n = 4. Then use the error bound
using Simpson's Rule with n = 4. Then use the error bound 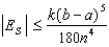 to estimate the accuracy.
to estimate the accuracy.
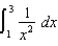 using Simpson's Rule with n = 4. Then use the error bound
using Simpson's Rule with n = 4. Then use the error bound 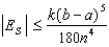 to estimate the accuracy.
to estimate the accuracy.
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
12
Use the Midpoint Rule with n = 2 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose using n = 10 to approximate the integral of a certain function by the Trapezoidal Rule results in an upper bound for the error equal to . What will the upper bound become if we change to n = 20?
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
14
Use Simpson's Rule with n = 4 to approximate 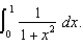
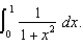

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
15
Use the Trapezoidal Rule with n = 2 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose using n = 10 to approximate the integral of a certain function by Simpson's Rule results in an upper bound for the error equal to . What will the upper bound become if we change to n = 20?
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
17
Use Simpson's Rule with n = 2 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
18
Use (a) the Trapezoidal Rule with n = 8 and (b) Simpson's Rule with n = 8 to approximate 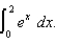 Round your answers to six decimal places.
Round your answers to six decimal places.
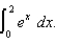 Round your answers to six decimal places.
Round your answers to six decimal places.
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
19
Use Simpson's Rule with n = 6 to approximate 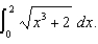
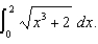

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
20
Use the Trapezoidal Rule with n = 1 to approximate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
21
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
22
Two students use Simpson's Rule to estimate 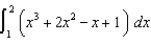 . One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
. One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
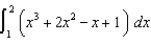 . One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
. One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
24
Find the value of the integral
A)1
B)
C)
D)2
E)
F)
G)
H)
A)1
B)
C)
D)2
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
25
Use the Table of Integrals in your textbook to evaluate each of the following:
(a)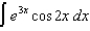 (b)
(b) 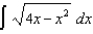 (c)
(c) 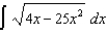 (d)
(d) 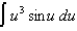 (e)
(e) 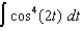 (f)
(f) 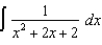 (g)
(g) 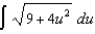 (h)
(h) 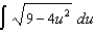 (i)
(i) 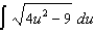 (j)
(j) 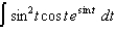
(a)
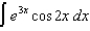 (b)
(b) 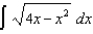 (c)
(c) 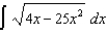 (d)
(d) 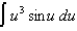 (e)
(e) 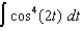 (f)
(f) 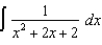 (g)
(g) 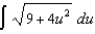 (h)
(h) 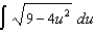 (i)
(i) 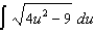 (j)
(j) 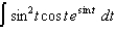

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
26
Find the partial fraction expansion of the rational function: .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
27
(a) Estimate 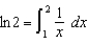 using Simpson's Rule with n = 4.(b) Estimate the error of the approximation in part (a).(c) How large should we take n to guarantee that the estimate by Simpson's Rule is accurate to within 0.001?
using Simpson's Rule with n = 4.(b) Estimate the error of the approximation in part (a).(c) How large should we take n to guarantee that the estimate by Simpson's Rule is accurate to within 0.001?
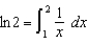 using Simpson's Rule with n = 4.(b) Estimate the error of the approximation in part (a).(c) How large should we take n to guarantee that the estimate by Simpson's Rule is accurate to within 0.001?
using Simpson's Rule with n = 4.(b) Estimate the error of the approximation in part (a).(c) How large should we take n to guarantee that the estimate by Simpson's Rule is accurate to within 0.001?
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
28
The following table shows the speedometer readings of a truck, taken at ten minute intervals during one hour of a trip.Time (min)
0
10
20
30
40
50
60
Speed (mi/h)
40
45
50
60
70
65
60
Use the table and the indicated technique to estimate the distance that the truck traveled in the hour.(a) The Trapezoidal Rule
(b) The Midpoint Rule
(c) Simpson's Rule
0
10
20
30
40
50
60
Speed (mi/h)
40
45
50
60
70
65
60
Use the table and the indicated technique to estimate the distance that the truck traveled in the hour.(a) The Trapezoidal Rule
(b) The Midpoint Rule
(c) Simpson's Rule

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
30
Below is a table of values for a continuous function f. 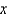
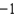
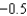 0
0
0.5
1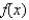 2.0
2.0
1.5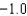 0.5
0.5 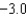 (a) Use the Trapezoidal Rule with n = 4 to approximate
(a) Use the Trapezoidal Rule with n = 4 to approximate 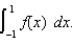 (b) Use Simpson's Rule with n = 4 to approximate
(b) Use Simpson's Rule with n = 4 to approximate 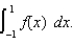
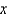
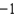
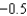 0
00.5
1
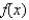 2.0
2.01.5
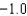 0.5
0.5 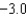 (a) Use the Trapezoidal Rule with n = 4 to approximate
(a) Use the Trapezoidal Rule with n = 4 to approximate 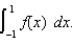 (b) Use Simpson's Rule with n = 4 to approximate
(b) Use Simpson's Rule with n = 4 to approximate 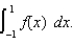

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
31
Use the Table of Integrals in your textbook to evaluate each of the following:
(a)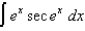 (b)
(b) 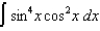 (c)
(c) 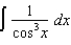 (d)
(d) 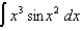 (e)
(e) 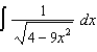 (f)
(f) 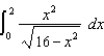 (g)
(g) 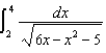 (h)
(h) 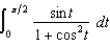 (i)
(i) 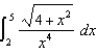 (j)
(j) 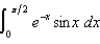
(a)
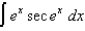 (b)
(b) 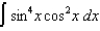 (c)
(c) 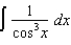 (d)
(d) 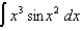 (e)
(e) 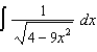 (f)
(f) 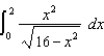 (g)
(g) 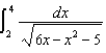 (h)
(h) 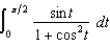 (i)
(i) 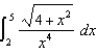 (j)
(j) 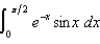

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
32
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
33
Intelligence Quotient (IQ) scores are assumed to be normally distributed in the population. The probability that a person selected at random from the general population will have an IQ between 100 and 120 is given by 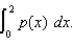 Use the graph of p (x) graphed below to answer the questions which follow:
Use the graph of p (x) graphed below to answer the questions which follow: 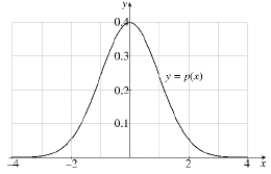 (a) Use Simpson's Rule with n = 4 to approximate
(a) Use Simpson's Rule with n = 4 to approximate 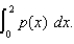 (b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by
(b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by 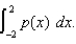 What is the approximate value of
What is the approximate value of 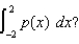 (c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
(c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
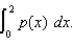 Use the graph of p (x) graphed below to answer the questions which follow:
Use the graph of p (x) graphed below to answer the questions which follow:  (a) Use Simpson's Rule with n = 4 to approximate
(a) Use Simpson's Rule with n = 4 to approximate 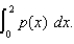 (b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by
(b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by 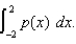 What is the approximate value of
What is the approximate value of 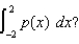 (c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
(c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
34
Find the value of the integral
A)1
B)
C)
D)2
E)
F)
G)
H)
A)1
B)
C)
D)2
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
35
Find the value of the integral
A)2
B)1
C)
D)
E)
F)
G)
H)
A)2
B)1
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
36
Find the value of the integral
A)1
B)
C)
D)2
E)3
F)
G)
H)
A)1
B)
C)
D)2
E)3
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
37
Two students use Simpson's Rule to estimate 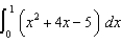 . One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
. One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
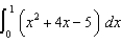 . One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
. One divides the interval into 30 equal subintervals and the other into 60 equal subintervals. How will the accuracy of their estimates compare?
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
38
The widths (in meters) of a kidney-shaped swimming pool were measured at 2-meter intervals as indicated in the figure. Use Simpson's Rule to estimate the area of the pool. 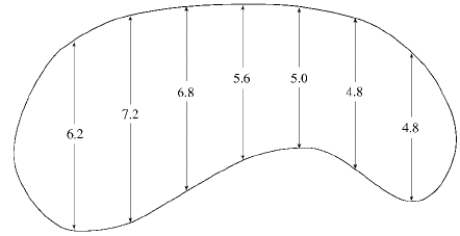


Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
39
A scientist collects the following data and plots it in the coordinate plane. 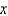 2
2
2.5
3
3.5
4
4.5
5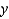 4
4
10
8
6
14
10
12
(a) Use Simpson's rule with n = 6 to estimate the area under the graph of a continuous function drawn through these points.(b) If it is known that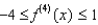 for all x, estimate the error involved in the approximation in part (a).(c) How large do we have to choose n so that the approximation
for all x, estimate the error involved in the approximation in part (a).(c) How large do we have to choose n so that the approximation 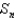 (Simpson's Rule) to the integral is accurate to within 0.001?
(Simpson's Rule) to the integral is accurate to within 0.001?
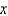 2
22.5
3
3.5
4
4.5
5
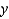 4
410
8
6
14
10
12
(a) Use Simpson's rule with n = 6 to estimate the area under the graph of a continuous function drawn through these points.(b) If it is known that
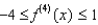 for all x, estimate the error involved in the approximation in part (a).(c) How large do we have to choose n so that the approximation
for all x, estimate the error involved in the approximation in part (a).(c) How large do we have to choose n so that the approximation 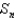 (Simpson's Rule) to the integral is accurate to within 0.001?
(Simpson's Rule) to the integral is accurate to within 0.001?
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
40
Find the value of the integral
A)1
B)
C)
D)2
E)
F)
G)
H)
A)1
B)
C)
D)2
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
41
Find the value of the integral
A)
B)
C)
D)
E)2
F)
11
G)
H)
A)
B)
C)
D)
E)2
F)
11
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
42
Find the value of the integral
A)
B)
C)2
D)
E)
F)1
G)
H)
A)
B)
C)2
D)
E)
F)1
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
43
Find the value of the integral
A)
B)
C)
D)4
E)2
F)
G)
H)
A)
B)
C)
D)4
E)2
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
44
Find the value of the integral
A)
B)
C)
D)1
E)
F)
G)
H)0
A)
B)
C)
D)1
E)
F)
G)
H)0

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the following integrals:
(a)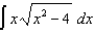 (b)
(b) 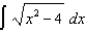 (c)
(c) 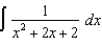 (d)
(d) 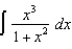
(a)
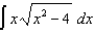 (b)
(b) 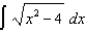 (c)
(c) 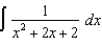 (d)
(d) 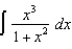

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
46
Find the partial fraction expansion of the rational function: .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
47
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the following integrals:
(a)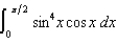 (b)
(b) 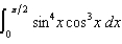 (c)
(c) 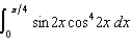 (d)
(d) 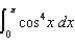
(a)
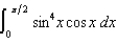 (b)
(b) 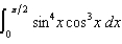 (c)
(c) 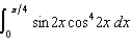 (d)
(d) 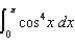

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
49
Find the value of the integral
A)
B)
C)
D)1
E)
F)
G)
H)0
A)
B)
C)
D)1
E)
F)
G)
H)0

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
50
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the following integrals:
(a)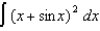 (b)
(b) 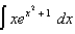 (c)
(c) 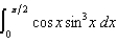 (d)
(d) 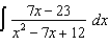
(a)
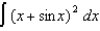 (b)
(b) 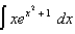 (c)
(c) 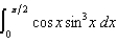 (d)
(d) 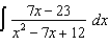

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
52
Find the partial fraction expansion of the rational function: .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
54
Find the value of the integral
A)
B)
C)
D)1
E)
F)
G)
H)0
A)
B)
C)
D)1
E)
F)
G)
H)0

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate the following integrals:
(a)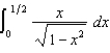 (b)
(b) 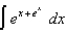 (c)
(c) 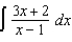 (d)
(d) 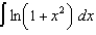
(a)
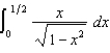 (b)
(b) 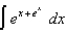 (c)
(c) 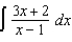 (d)
(d) 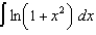

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
56
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the following integrals:
(a)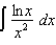 (b)
(b) 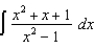 (c)
(c) 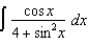 (d)
(d) 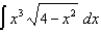
(a)
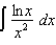 (b)
(b) 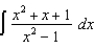 (c)
(c) 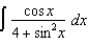 (d)
(d) 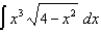

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the following integrals:
(a)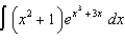 (b)
(b) 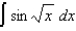 (c)
(c) 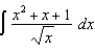 (d)
(d) 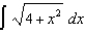
(a)
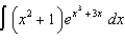 (b)
(b) 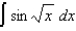 (c)
(c) 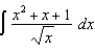 (d)
(d) 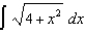

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the following integrals:
(a)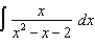 (b)
(b) 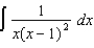 (c)
(c) 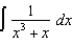 (d)
(d) 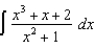
(a)
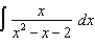 (b)
(b) 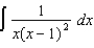 (c)
(c) 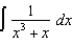 (d)
(d) 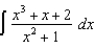

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
60
Find the value of the integral
A)2
B)
C)1
D)
E)
F)
G)
H)
A)2
B)
C)1
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
62
Find the value of
A)
B)
C)
D)
E)1
F)
G)0
H)
A)
B)
C)
D)
E)1
F)
G)0
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
63
Find the value of the integral
A).0
B)1
C)
D)
E)
F)2
G)
H)
A).0
B)1
C)
D)
E)
F)2
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
64
Determine a reduction formula for 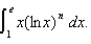
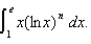

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate the following integrals:
(a)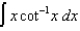 (b)
(b) 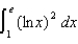 (c)
(c) 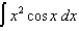 (d)
(d) 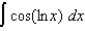
(a)
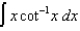 (b)
(b) 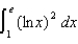 (c)
(c) 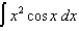 (d)
(d) 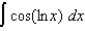

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
66
Find the value of the integral
A)4
B)
C)3
D)
E)
F)2
G)
H)5
A)4
B)
C)3
D)
E)
F)2
G)
H)5

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
67
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
68
(a) Use integration by parts to prove the reduction formula: 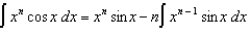 (b) Demonstrate your understanding of this formula by using it to evaluate:
(b) Demonstrate your understanding of this formula by using it to evaluate: 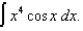
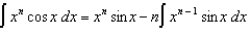 (b) Demonstrate your understanding of this formula by using it to evaluate:
(b) Demonstrate your understanding of this formula by using it to evaluate: 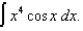

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate the following integrals:
(a)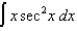 (b)
(b) 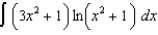 (c)
(c) 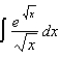 (d)
(d) 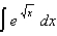
(a)
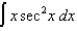 (b)
(b) 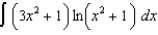 (c)
(c) 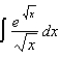 (d)
(d) 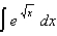

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the following integrals:
(a)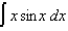 (b)
(b) 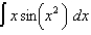 (c)
(c) 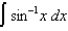 (d)
(d) 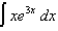
(a)
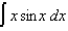 (b)
(b) 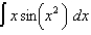 (c)
(c) 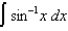 (d)
(d) 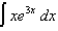

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
71
Find the value of the integral
A)
B)2
C)
D)
E)
F)
G)
H)1
A)
B)2
C)
D)
E)
F)
G)
H)1

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
72
Find the value of the integral
A)
B)
C)sin 1
D)1 - cos 1
E)
F)
G)
H)1 + tan 1
A)
B)
C)sin 1
D)1 - cos 1
E)
F)
G)
H)1 + tan 1

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
74
Find the value of the integral
A)0
B)1
C)
D)
E)
F)2
G)
H)
A)0
B)1
C)
D)
E)
F)2
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
75
Find the value of
A)0
B)1
C)2
D)3
E)4
F)5
G)6
H)7
A)0
B)1
C)2
D)3
E)4
F)5
G)6
H)7

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the following integrals:
(a)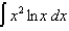 (b)
(b) 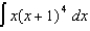 (c)
(c) 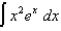 (d)
(d) 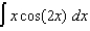
(a)
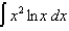 (b)
(b) 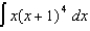 (c)
(c) 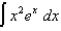 (d)
(d) 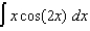

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
77
Let f be a twice differentiable function such that f(0) = 5, f(3) = 1, and 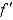 (3) =
(3) = 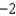 . Determine the value of
. Determine the value of 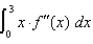 .
.
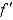 (3) =
(3) = 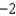 . Determine the value of
. Determine the value of 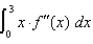 .
.
Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
78
Find the value of the integral
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
79
Find the value of the integral
A)
B)
C)0
D)
E)
F)
G)
H)Does not exist
A)
B)
C)0
D)
E)
F)
G)
H)Does not exist

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 239 flashcards in this deck.
Unlock Deck
k this deck


