Exam 5: Integrals
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find the partial fraction expansion of the rational function: .
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
G
Let f (x) = on the interval [ - 1,1]. Let the interval be divided into four equal subintervals. Find the value of the Riemann sum is the left endpoint of its subinterval.
Free
(Multiple Choice)
4.8/5  (45)
(45)
Correct Answer:
A
Given the graph below, use 5 rectangles to estimate the area under the graph from x = 0 to x = 5. Compute L5 (sample points are left endpoints), R5 (sample points are right endpoints) and M5 (sample points are midpoints). Which of the estimates appears to give the best estimate? Justify your answer. 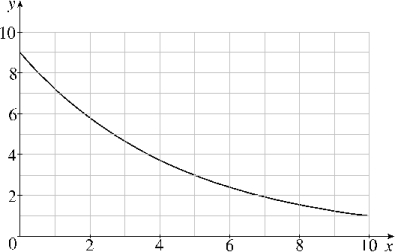
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
L5 44.8; R5 28.8; M5 36.2; Since the graph of the function is decreasing, using midpoints appears to give the best approximation.
Let (a) Find an expression for g (x) similar to the one for f (x).(b) Where is f differentiable? Where is g differentiable?
(Essay)
4.8/5  (36)
(36)
What is the value of the estimate using four approximating rectangles and taking sample points to be right-hand endpoints?
(Multiple Choice)
4.8/5  (40)
(40)
Given the graph of below: ![Given the graph of y = h ( x ) below: (a) Find c in [0,6] which will maximize \int _ { 0 } ^ { c } h ( x ) d x (b) Show that \int _ { - 1 } ^ { 3 } h ( x ) d x is between 4 and 7.](https://storage.examlex.com/TB2033/11eaa8e2_0e95_6bc7_96ab_f33330817947_TB2033_00.jpg) (a) Find c in [0,6] which will maximize (b) Show that is between 4 and 7.
(a) Find c in [0,6] which will maximize (b) Show that is between 4 and 7.
(Essay)
4.8/5  (37)
(37)
A particle travels along a line. Its velocity in meters per second is given by Find
(a) the displacement from t = 0 to t = 8.(b) the distance traveled by the particle from t = 0 to t = 8.
(Short Answer)
4.7/5  (22)
(22)
Suppose we wish to estimate the area under the curve y = x between x = 1 and x = 2 using 2 subintervals of equal length. What is the largest value the approximation could have?
(Multiple Choice)
4.9/5  (36)
(36)
Intelligence Quotient (IQ) scores are assumed to be normally distributed in the population. The probability that a person selected at random from the general population will have an IQ between 100 and 120 is given by Use the graph of p (x) graphed below to answer the questions which follow: 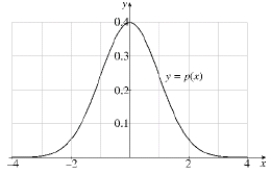 (a) Use Simpson's Rule with n = 4 to approximate
(b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by What is the approximate value of (c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
(a) Use Simpson's Rule with n = 4 to approximate
(b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by What is the approximate value of (c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
(Essay)
4.8/5  (35)
(35)
Use the Midpoint Rule with 2 equal subdivisions to get an approximation for ln 5.
(Short Answer)
4.8/5  (38)
(38)
Use (a) the Trapezoidal Rule with n = 8 and (b) Simpson's Rule with n = 8 to approximate Round your answers to six decimal places.
(Essay)
4.8/5  (34)
(34)
Given functions of and , use the facts that , to evaluate the following integrals:
(a) (b) (c) (d)
(Essay)
4.9/5  (40)
(40)
Showing 1 - 20 of 239
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)