Deck 12: Multiple Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/270
Play
Full screen (f)
Deck 12: Multiple Integrals
1
Find the Jacobian of the transformation 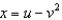 ,
, 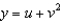 .
.
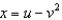 ,
, 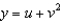 .
.4v
2
Find the Jacobian of the transformation , , .
A)
B)
C)
D)
E)2
F)
G)
H)
A)
B)
C)
D)
E)2
F)
G)
H)
3
Find the Jacobian of the transformation 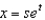 ,
, 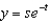 .
.
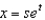 ,
, 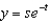 .
.-2s
4
Evaluate the integral , where R is the region enclosed by the ellipse .
A)24
B)
C)12
D)3
E)10
F)2
G)6
H)4
A)24
B)
C)12
D)3
E)10
F)2
G)6
H)4

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
5
Find the Jacobian of the transformation , .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
6
Find the Jacobian of the transformation x = 3u + v, y = u - 2w, z = v + w.
A)1
E)-1
B)6
F)-6
C)-5
G)5
D)4
H)-4
A)1
E)-1
B)6
F)-6
C)-5
G)5
D)4
H)-4

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
7
Find the area of the region whose image under the transformation x = u + v, y = v - 2u is .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the integral , where R is the triangular region with vertices (1, 0), (0, -1), and (0, 0).
A)0
B)
C)
D)
E)1
F)
G)2
H)-2
A)0
B)
C)
D)
E)1
F)
G)2
H)-2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
9
Find the Jacobian of the transformation , , when and v = 1.
A)1
B)2
C)3
D)6
E)-1
F)-2
G)-3
H)-6
A)1
B)2
C)3
D)6
E)-1
F)-2
G)-3
H)-6

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
10
Find the Jacobian of the transformation x = u + v, y = 2u - v.
A)1
E)-1
B)2
F)-2
C)3
G)-3
D)4
H)-4
A)1
E)-1
B)2
F)-2
C)3
G)-3
D)4
H)-4

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
11
Use the change of variables u = 2x - y, v = x + y to evaluate 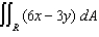 where R is the region bounded by 2x - y = 1, 2x - y = 3, x + y = 1, and x + y = 2.
where R is the region bounded by 2x - y = 1, 2x - y = 3, x + y = 1, and x + y = 2.
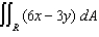 where R is the region bounded by 2x - y = 1, 2x - y = 3, x + y = 1, and x + y = 2.
where R is the region bounded by 2x - y = 1, 2x - y = 3, x + y = 1, and x + y = 2.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
12
Find the Jacobian of the transformation x = u, y = 2v, z = 3w.
A)1
E)-1
B)2
F)-2
C)3
G)-3
D)6
H)-6
A)1
E)-1
B)2
F)-2
C)3
G)-3
D)6
H)-6

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
13
Use the change of variables 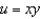 ,
, 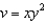 to evaluate
to evaluate 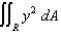 , where R is the region bounded by the curves xy = 1, xy = 2,
, where R is the region bounded by the curves xy = 1, xy = 2, 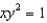 , and
, and 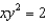 .
.
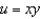 ,
, 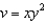 to evaluate
to evaluate 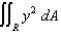 , where R is the region bounded by the curves xy = 1, xy = 2,
, where R is the region bounded by the curves xy = 1, xy = 2, 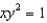 , and
, and 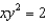 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
14
Under the transformation x = u + v, y = v - 2u, the image of the circle is an ellipse. What is the area of that ellipse?
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
15
Use the change of variables x = 2u + 3v, y = 3u - 2v to evaluate 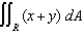 , where R is the square with vertices (0, 0), (2, 3), (5, 1), and (3, -2).
, where R is the square with vertices (0, 0), (2, 3), (5, 1), and (3, -2).
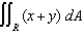 , where R is the square with vertices (0, 0), (2, 3), (5, 1), and (3, -2).
, where R is the square with vertices (0, 0), (2, 3), (5, 1), and (3, -2).
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
16
Find the Jacobian of the transformation x = u sin v, y = u cos v when u = 3 and v = 5.
A)3
E)-3
B)5
F)-5
C)7.5
G)-7.5
D)15
H)-15
A)3
E)-3
B)5
F)-5
C)7.5
G)-7.5
D)15
H)-15

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
17
Find the Jacobian of the transformation , , z = z.
A)
B)z
C)r
D)1
E)2
F)2z
G)2r
H)2
A)
B)z
C)r
D)1
E)2
F)2z
G)2r
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
18
Find the Jacobian of the transformation x = 2u, 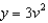 ,
, 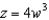 .
.
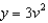 ,
, 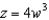 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
19
Find the Jacobian of the transformation , .
A)
B)
C)u
D)
E)
F)
G)
H)
A)
B)
C)u
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
20
Use the change of variables 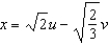 ,
, 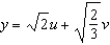 to evaluate
to evaluate 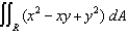 , where R is the region bounded by the ellipse
, where R is the region bounded by the ellipse 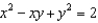 .
.
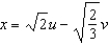 ,
, 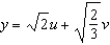 to evaluate
to evaluate 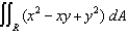 , where R is the region bounded by the ellipse
, where R is the region bounded by the ellipse 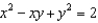 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate 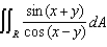 ,where R is the rectangular region bounded by the lines x + y = 0,
,where R is the rectangular region bounded by the lines x + y = 0, 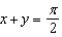 , x - y = 0, and
, x - y = 0, and 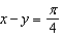 .
.
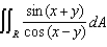 ,where R is the rectangular region bounded by the lines x + y = 0,
,where R is the rectangular region bounded by the lines x + y = 0, 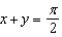 , x - y = 0, and
, x - y = 0, and 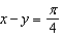 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the iterated integral .
A)
B)
C)
D)2
E)
F)
G)
H)
A)
B)
C)
D)2
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
23
Find a transformation x = x (u, v), y = y (u, v) maps the region in the uv-plane into the xy-plane. 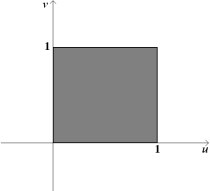
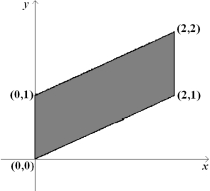



Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
24
Let T be the transformation given by x = 2u + v, y = u + 2v.(a) A region S in the uv-plane is given below. Sketch the image R of S in the xy-plane. 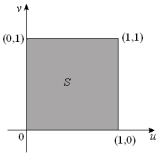 (b) Find the inverse transformation
(b) Find the inverse transformation 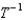 .(c) Evaluate the double integral
.(c) Evaluate the double integral 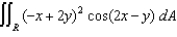 .
.
 (b) Find the inverse transformation
(b) Find the inverse transformation  .(c) Evaluate the double integral
.(c) Evaluate the double integral 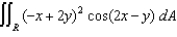 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate 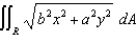 , where R is the region enclosed by the ellipse
, where R is the region enclosed by the ellipse 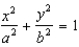 .
.
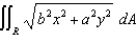 , where R is the region enclosed by the ellipse
, where R is the region enclosed by the ellipse 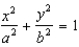 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
26
Compute the Jacobian of the transformation T given by 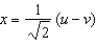 ,
, 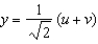 , and find the image of
, and find the image of 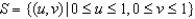 under T.
under T.
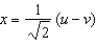 ,
, 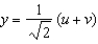 , and find the image of
, and find the image of 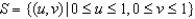 under T.
under T.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
27
Let T be the transformation given by x = 2u + v, y = 3u.(a) A region S in the uv-plane is given below. Sketch the image R of S in the xy-plane. 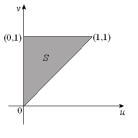 (b) Find the inverse transformation
(b) Find the inverse transformation 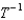 .(c) Evaluate the double integral
.(c) Evaluate the double integral 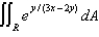 .
.
 (b) Find the inverse transformation
(b) Find the inverse transformation 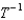 .(c) Evaluate the double integral
.(c) Evaluate the double integral 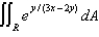 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
28
Compute the Jacobian of the transformation T given by 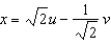 ,
, 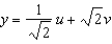 . Compute the area of the image of
. Compute the area of the image of 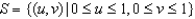 and compare it to the area of S.
and compare it to the area of S.
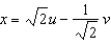 ,
, 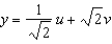 . Compute the area of the image of
. Compute the area of the image of 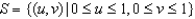 and compare it to the area of S.
and compare it to the area of S.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate 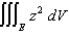 , where E is the solid bounded by the ellipsoid
, where E is the solid bounded by the ellipsoid 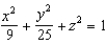 .
.
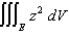 , where E is the solid bounded by the ellipsoid
, where E is the solid bounded by the ellipsoid 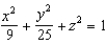 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
30
Describe the image R of the set 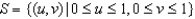 under the transformation
under the transformation 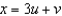 ,
, 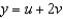 , and then compute
, and then compute 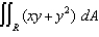 .
.
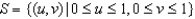 under the transformation
under the transformation 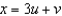 ,
, 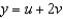 , and then compute
, and then compute 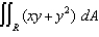 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
31
Find a transformation x = x (u, v), y = y (u, v) maps the region in the uv-plane into the xy-plane. 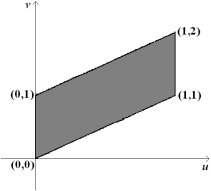
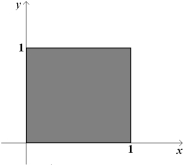



Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the iterated integral .
A)
B)
C)
D)2
E)
F)
G)
H)
A)
B)
C)
D)2
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the iterated integral .
A)
B)
C)4
D)12
E)
F)
G)
H)
A)
B)
C)4
D)12
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
34
Use the change of variables 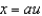 ,
, 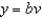 ,
, 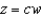 to evaluate
to evaluate 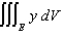 , where E is the solid enclosed by the ellipsoid
, where E is the solid enclosed by the ellipsoid 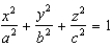 .
.
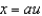 ,
, 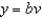 ,
, 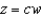 to evaluate
to evaluate 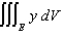 , where E is the solid enclosed by the ellipsoid
, where E is the solid enclosed by the ellipsoid 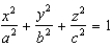 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate 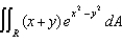 ,where R is the rectangular region bounded by the lines x + y = 0, x + y = 1, x - y = 0, and x - y = 1.
,where R is the rectangular region bounded by the lines x + y = 0, x + y = 1, x - y = 0, and x - y = 1.
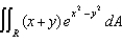 ,where R is the rectangular region bounded by the lines x + y = 0, x + y = 1, x - y = 0, and x - y = 1.
,where R is the rectangular region bounded by the lines x + y = 0, x + y = 1, x - y = 0, and x - y = 1.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
36
Find a transformation x = x (u, v), y = y (u, v) maps the region in the uv-plane into the xy-plane. 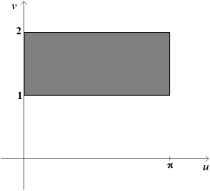
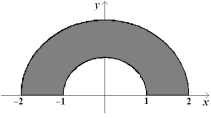



Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate the triple integral in cylindrical coordinates, where .
A)
B)
C)
D)
E)
F)
G)
H)2
A)
B)
C)
D)
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate the triple integral in cylindrical coordinates, where .
A)
B)
C)
D)
E)
F)
G)
H)2
A)
B)
C)
D)
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate 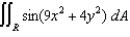 by making an appropriate change of variables, where R is the region in the first quadrant bounded by the ellipse
by making an appropriate change of variables, where R is the region in the first quadrant bounded by the ellipse 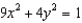 .
.
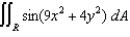 by making an appropriate change of variables, where R is the region in the first quadrant bounded by the ellipse
by making an appropriate change of variables, where R is the region in the first quadrant bounded by the ellipse 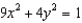 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
40
Compute the Jacobian of the transformation T given by , . Describe the image of , and compute its area.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
41
A sphere of radius k has a volume of 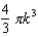 . Set up the iterated integrals in rectangular, cylindrical, and spherical coordinates to show this.
. Set up the iterated integrals in rectangular, cylindrical, and spherical coordinates to show this.
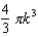 . Set up the iterated integrals in rectangular, cylindrical, and spherical coordinates to show this.
. Set up the iterated integrals in rectangular, cylindrical, and spherical coordinates to show this.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the triple integral in spherical coordinates, where E is the solid bounded by the hemisphere and the plane z = 0.
A)
B)16
C)
D)
E)
F)8
G)
H)2
A)
B)16
C)
D)
E)
F)8
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate 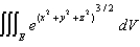 , where E is the solid bounded by the sphere
, where E is the solid bounded by the sphere 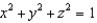 .
.
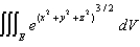 , where E is the solid bounded by the sphere
, where E is the solid bounded by the sphere 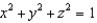 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
44
Find the volume bounded above by the surface 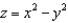 ,
, 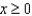 , below by the xy-plane, and laterally by the cylinder
, below by the xy-plane, and laterally by the cylinder 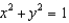 .
.
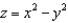 ,
, 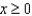 , below by the xy-plane, and laterally by the cylinder
, below by the xy-plane, and laterally by the cylinder 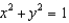 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
45
Use cylindrical coordinates to find 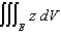 , where R is the region bounded by
, where R is the region bounded by 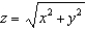 and
and 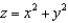 .
.
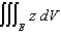 , where R is the region bounded by
, where R is the region bounded by 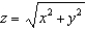 and
and 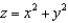 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
46
Find the mass of the solid that occupies the region bounded by , z = 2, and z = 0 and has density function .
A)
B)
C)
D)
E)
F)
G)
H)2
A)
B)
C)
D)
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate 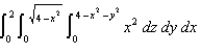 by changing to cylindrical coordinates.
by changing to cylindrical coordinates.
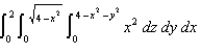 by changing to cylindrical coordinates.
by changing to cylindrical coordinates.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the triple integral , where .
A)
B)
C)
D)
E)2
F)
G)
H)
A)
B)
C)
D)
E)2
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate 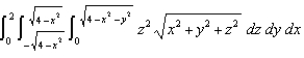 by changing to spherical coordinates.
by changing to spherical coordinates.
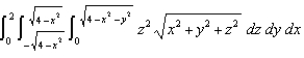 by changing to spherical coordinates.
by changing to spherical coordinates.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
50
Find the volume of the region above the paraboloid 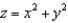 and below the hemisphere
and below the hemisphere 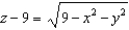 .
.
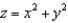 and below the hemisphere
and below the hemisphere 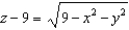 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the iterated integral .
A)
B)
C)4
D)2
E)
F)
G)
H)
A)
B)
C)4
D)2
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the triple integral in spherical coordinates, where E is the solid in the first octant bounded by the sphere and the coordinate planes.
A)
B)
C)
D)
E)
F)
G)
H)2
A)
B)
C)
D)
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
53
Find the mass of the solid that occupies the region bounded by the paraboloid and the plane z = 1 and has density function .
A)
B)
C)
D)
E)
F)
G)
H)2
A)
B)
C)
D)
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
54
Find the mass of that portion of the solid bounded above by the sphere 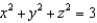 which lies in the first octant, if the density varies as the distance from the center of the sphere.
which lies in the first octant, if the density varies as the distance from the center of the sphere.
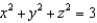 which lies in the first octant, if the density varies as the distance from the center of the sphere.
which lies in the first octant, if the density varies as the distance from the center of the sphere.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
55
A region W in 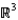 is described completely by
is described completely by 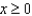 ,
, 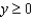 ,
, 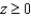 , and
, and 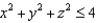 .(a) Describe or sketch this region.
.(a) Describe or sketch this region. 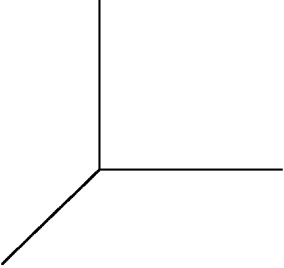 (b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.
(b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.
 is described completely by
is described completely by 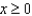 ,
, 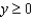 ,
, 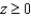 , and
, and 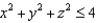 .(a) Describe or sketch this region.
.(a) Describe or sketch this region.  (b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.
(b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate 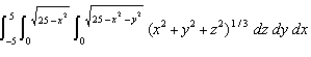 by changing to spherical coordinates.
by changing to spherical coordinates.
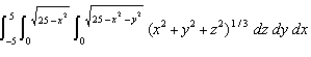 by changing to spherical coordinates.
by changing to spherical coordinates.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate 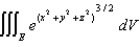 , where E is the solid bounded by the sphere
, where E is the solid bounded by the sphere 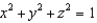 and the cone
and the cone 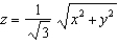 .
.
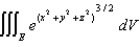 , where E is the solid bounded by the sphere
, where E is the solid bounded by the sphere 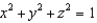 and the cone
and the cone 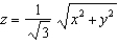 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
58
Use a triple integral in spherical coordinates to find the volume of that part of the sphere 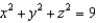 which lies inside the cone
which lies inside the cone 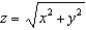 .
.
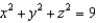 which lies inside the cone
which lies inside the cone 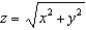 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
59
Let E be the solid that lies below the sphere and above the cone , where . Find the value of the triple integral .
A)
B).
C)
D)
E)
F)
G)
H)
A)
B).
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
60
Find the volume of the region inside the cylinder 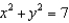 which is bounded below by the xy-plane and above by the sphere
which is bounded below by the xy-plane and above by the sphere 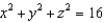 .
.
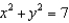 which is bounded below by the xy-plane and above by the sphere
which is bounded below by the xy-plane and above by the sphere 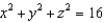 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the iterated integral .
A)6
B)1
C)3
D)2
E)-6
F)-1
G)-3
H)-2
A)6
B)1
C)3
D)2
E)-6
F)-1
G)-3
H)-2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the iterated integral .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
63
Give a geometric description of the solid S whose volume in cylindrical coordinates is given by 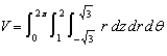 .
.
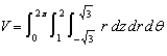 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
64
Find the mass of the solid that occupies the region and has density function .
A)
B)
C)
D)
E)
F)
G)
H)1
A)
B)
C)
D)
E)
F)
G)
H)1

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
65
Find the mass of a solid ball of radius 2 if the density at each point (x, y, z) is 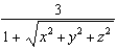 .
.
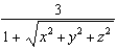 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the iterated integral .
A)
B)2
C)4
D)16
E)12
F)
G)48
H)8
A)
B)2
C)4
D)16
E)12
F)
G)48
H)8

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the iterated integral .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate the iterated integral .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
69
Let E be the part of the solid ellipsoid 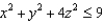 that lies in the first octant above
that lies in the first octant above
the plane z = 1.(a) Express the triple integral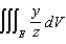 as an iterated integral in rectangular coordinates.(b) Express the triple integral
as an iterated integral in rectangular coordinates.(b) Express the triple integral 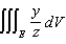 as an iterated integral in cylindrical coordinates.(c) Express the triple integral
as an iterated integral in cylindrical coordinates.(c) Express the triple integral 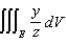 as an iterated integral in spherical coordinates.
as an iterated integral in spherical coordinates.
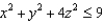 that lies in the first octant above
that lies in the first octant abovethe plane z = 1.(a) Express the triple integral
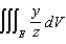 as an iterated integral in rectangular coordinates.(b) Express the triple integral
as an iterated integral in rectangular coordinates.(b) Express the triple integral 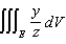 as an iterated integral in cylindrical coordinates.(c) Express the triple integral
as an iterated integral in cylindrical coordinates.(c) Express the triple integral 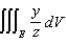 as an iterated integral in spherical coordinates.
as an iterated integral in spherical coordinates.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the triple integral , where .
A)
B)
C)
D)
E)
F)
G)
H)1
A)
B)
C)
D)
E)
F)
G)
H)1

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate the iterated integral .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
72
Sketch the region E whose volume is given by the integral 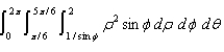 .
. 
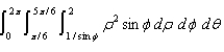 .
. 

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate the triple integral , where E is the solid bounded by the coordinate planes and the plane 2x + y + z = 4.
A)1
B)
C)
D)
E)
F)
G)
H)
A)1
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
74
Evaluate 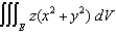 , where E is the solid bounded by the cylinder
, where E is the solid bounded by the cylinder 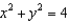 , above by z = 3 and below by z = 0.
, above by z = 3 and below by z = 0.
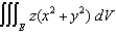 , where E is the solid bounded by the cylinder
, where E is the solid bounded by the cylinder 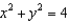 , above by z = 3 and below by z = 0.
, above by z = 3 and below by z = 0.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
75
Let E be the solid bounded above by the sphere 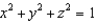 and below by the cone
and below by the cone 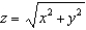 .(a) Express the volume of E as an iterated integral in rectangular coordinates.(b) Express the volume of E as an iterated integral in cylindrical coordinates.(c) Express the volume of E as an iterated integral in spherical coordinates.
.(a) Express the volume of E as an iterated integral in rectangular coordinates.(b) Express the volume of E as an iterated integral in cylindrical coordinates.(c) Express the volume of E as an iterated integral in spherical coordinates.
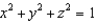 and below by the cone
and below by the cone 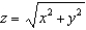 .(a) Express the volume of E as an iterated integral in rectangular coordinates.(b) Express the volume of E as an iterated integral in cylindrical coordinates.(c) Express the volume of E as an iterated integral in spherical coordinates.
.(a) Express the volume of E as an iterated integral in rectangular coordinates.(b) Express the volume of E as an iterated integral in cylindrical coordinates.(c) Express the volume of E as an iterated integral in spherical coordinates.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the iterated integral .
A)0
B)8
C)4
D)16
E)6
F)2
G)5
H)1
A)0
B)8
C)4
D)16
E)6
F)2
G)5
H)1

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate the triple integral , where E is the wedge in the first octant bounded by , y = x, and the yz-plane.
A)
B)
C)
D)
E)
F)1
G)
H)
A)
B)
C)
D)
E)
F)1
G)
H)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate the triple integral , where .
A)
B)
C)
D)1
E)
F)
G)
H)2
A)
B)
C)
D)1
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate the iterated integral .
A)
B)8
C)4
D)16
E)
F)2
G)5
H)1
A)
B)8
C)4
D)16
E)
F)2
G)5
H)1

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
80
Give a geometric description of the solid S whose volume in spherical coordinates is given by 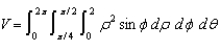 .
.
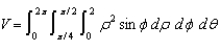 .
.
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck


