Deck 6: Network Optimization Problems

Question 1

Each node in a minimum cost flow problem where the net amount of flow generated is a fixed positive number is a demand node.

Answer 1

False

Question 2

In a feasible minimum cost flow problem, the network has enough arcs with sufficient capacity to enable all the flow generated at the supply nodes to reach all the demand nodes.

Answer 2

True

Question 3

The network simplex method can be used to solve minimum cost flow problems with over a million arcs.

Answer 3

True

Question 4

A minimum cost flow problem may be summarized by drawing a network only after writing out the full formulation.

Question 5

Any node where the net amount of flow generated is fixed at zero is a transshipment node.

Question 6

Conservation of flow is achieved when the flow through a node is minimized.

Question 7

All network optimization problems actually are special types of linear programming problems.

Question 8

The network simplex method can aid managers in conducting what-if analysis.

Question 9

The amount of flow that is eventually sent through an arc is called the capacity of that arc.

Question 10

As long as all its supplies and demands have integer values, any minimum cost flow problem is guaranteed to have an optimal solution with integer values.

Question 11

A network representation is a very specific conceptual aid and is only used in special cases.

Question 12

A transportation problem is just a minimum cost flow problem without any transshipment nodes and without any capacity constraints on the arcs.

Question 13

The objective of a minimum cost flow problem is to minimize the total cost of sending the available supply through the network even if all demand is not satisfied.

Question 14

In a minimum cost flow problem there can be only one supply node and only one demand node.

Question 15

The model for any minimum cost flow problem is represented by a network with flow passing through it.

Question 16

A minimum cost flow problem will have feasible solutions as long as there is a balance between the total supply from the supply nodes and the total demand at the demand nodes.

Question 17

Any minimum cost flow problem where each arc can carry any desired amount of flow is a transshipment problem.

Question 18

Minimum cost flow problems are the special type of linear programming problem referred to as distribution-network problems.

Question 19

In a minimum cost flow problem, the cost of the flow through each arc is proportional to the amount of that flow.

Question 20

Network representations can be used for financial planning.

Question 21

The source and sink of a maximum flow problem have conservation of flow.

Question 22

The source and sink of a maximum flow problem are analogous to the supply nodes and demand nodes of a minimum cost flow problem.

Question 23

A shortest path problem is required to have only a single destination.

Question 24

A minimum cost flow problem is a special type of:

A) linear programming problem.
B) transportation problem.
C) spanning tree problem.
D) transshipment problem.
E) maximum flow problem.

Question 25

Which of the following is an example of a transshipment node?

A) Storage facilities
B) Processing facilities
C) Short-term investment options
D) Warehouses
E) All of the choices are correct.

Question 26

Which of the following will have negative net flow in a minimum cost flow problem?

A) Supply nodes
B) Transshipment nodes
C) Demand nodes
D) Arc capacities
E) None of the choices is correct.

Question 27

In a shortest path problem, the lines connecting the nodes are referred to as arcs.

Question 28

When reformulating a shortest path problem as a minimum cost flow problem, each link should be replaced by a pair of arcs pointing in opposite directions.

Question 29

The objective of a maximum flow problem is to maximize the total profit generated by sending flow through a network.

Question 30

In a shortest path problem there are no arcs permitted, only links.

Question 31

In a maximum flow problem, flow is permitted in both directions and is represented by a pair of arcs pointing in opposite directions.

Question 32

Which of the following can be used to optimally solve minimum cost flow problems?
I) The simplex method.
II) The network simplex method.
III) A greedy algorithm.

A) I only.
B) II only.
C) III only.
D) I and II only.
E) All of these.

Question 33

Which of the following is not an assumption of a minimum cost flow problem?

A) At least one of the nodes is a supply node.
B) There is an equal number of supply and demand nodes.
C) Flow through an arc is only allowed in the direction indicated by the arrowhead.
D) The cost of the flow through each arc is proportional to the amount of that flow.
E) The objective is either to minimize the total cost or to maximize the total profit.

Question 34

Shortest path problems are concerned with finding the shortest route through a network.

Question 35

In a maximum flow problem, the source and sink have fixed supplies and demands.

Question 36

A maximum flow problem can be fit into the format of a minimum cost flow problem.

Question 37

Network representations can be used for the following problems:

A) project planning.
B) facilities location.
C) financial planning.
D) resource management.
E) All of the choices are correct.

Question 38

A network model showing the geographical layout of the problem is the usual way to represent a shortest path problem.

Question 39

Maximum flow problems are concerned with maximizing the flow of goods through a distribution network.

Question 40

In a true maximum flow problem there is only one source and one sink.

Question 41

Which of the following could be the subject of a maximum flow problem?

A) Products
B) Oil
C) Vehicles
D) All of the choices are correct.
E) None of the choices is correct.

Question 42

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\\text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array}$$
Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the optimal quantity to ship from Factory B to Customer 3?

A) 25 units
B) 50 units
C) 75 units
D) 100 units
E) 125 units

Question 43

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\\text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array}$$
How many demand nodes are present in this problem?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 44

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\\text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array}$$
Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the minimum total cost to meet all customer requirements?

A) $4,475
B) $4,500
C) $4,775
D) $4,950
E) $5,150

Question 45

Which of the following problems are special types of minimum cost flow problems?
I) Transportation problems.
II) Assignment problems.
III) Transshipment problems.
IV) Shortest path problems.

A) I and II only
B) I, II, and III only
C) IV only
D) I, II, III, and IV
E) None of the choices is correct.

Question 46

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\\text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array}$$
How many arcs will the network have?

A) 3
B) 4
C) 7
D) 12
E) 15

Question 47

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\\text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array}$$
How many supply nodes are present in this problem?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 48

Which of the following is not an assumption of a shortest path problem?

A) The lines connecting certain pairs of nodes always allow travel in either direction.
B) Associated with each link or arc is a nonnegative number called its length.
C) A path through the network must be chosen going from the origin to the destination.
D) The objective is to find a shortest path from the origin to the destination.
E) None of the choices is correct.

Question 49

In a shortest path problem, when "real travel" through a network can end at more than one node:
I) An arc with length 0 is inserted.
II) The problem cannot be solved.
III) A dummy destination is needed.

A) I only.
B) II only.
C) III only.
D) I and II only.
E) I and III only.

Question 50

Which of the following is not an assumption of a maximum flow problem?

A) All flow through the network originates at one node, called the source.
B) If a node is not the source or the sink then it is a transshipment node.
C) Flow can move toward the sink and away from the sink.
D) The maximum amount of flow through an arc is given by the capacity of the arc.
E) The objective is to maximize the total amount of flow from the source to the sink.

Question 51

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\\text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array}$$
How many supply nodes are present in this problem?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 52

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\\text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array}$$
Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the minimum total cost to meet all customer requirements?

A) $8,750
B) $8,950
C) $9,000
D) $9,100
E) $10,050

Question 53

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\\text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array}$$
Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the optimal quantity to ship from Factory A to Customer 2?

A) 25 units
B) 50 units
C) 75 units
D) 100 units
E) 125 units

Question 54

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\\text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array}$$
How many demand nodes are present in this problem?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 55

Which of the following is an application of a shortest path problem?
I) Minimize total distance traveled.
II) Minimize total flow through a network.
III) Minimize total cost of a sequence of activities.
IV) Minimize total time of a sequence of activities

A) I and II only
B) I, II, and III only.
C) IV only
D) I, II, III, and IV
E) I, III, and IV only.

Question 56

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\\text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array}$$
Which type of network optimization problem is used to solve this problem?

A) Maximum-Cost Flow problem
B) Minimum-Cost Flow problem
C) Maximum Flow Problem
D) Minimum Flow Problem
E) Shortest Path Problem

Question 57

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\\text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array}$$
How many arcs will the network have?

A) 3
B) 4
C) 7
D) 12
E) 16

Question 58

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:
$$\text{Customer (requirement)}\\\begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\\text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array}$$
Which type of network optimization problem is used to solve this problem?

A) Maximum-Cost Flow problem
B) Minimum-Cost Flow problem
C) Maximum Flow Problem
D) Minimum Flow Problem
E) Shortest Path Problem

Question 59

For a minimum cost flow problem to have a feasible solution, which of the following must be true?

A) There is the same number of supply nodes and demand nodes.
B) There is only one supply node and one demand node.
C) There is an equal amount of supply and demand.
D) The supply and demand must be integers.
E) The transshipment nodes must be able to absorb flow.

Question 60

What is the objective of a maximum flow problem?

A) Maximize the amount flowing through a network.
B) Maximize the profit of the network.
C) Maximize the routes being used.
D) Maximize the amount produced at the origin.
E) None of the choices is correct.

Question 61

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 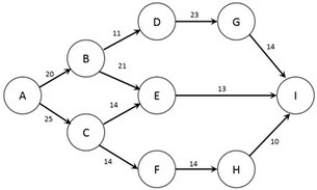Which type of network optimization problem is used to solve this problem?

A) Maximum-Cost Flow problem
B) Minimum-Cost Flow problem
C) Maximum Flow Problem
D) Minimum Flow Problem
E) Shortest Path Problem

Question 62

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 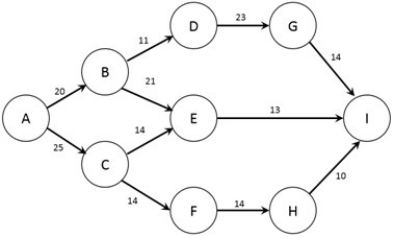What is the capacity of the connection between nodes B and E?

A) 9 packages/day
B) 11 packages/day
C) 16 packages/day
D) 21 packages/day
E) 26 packages/day

Question 63

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 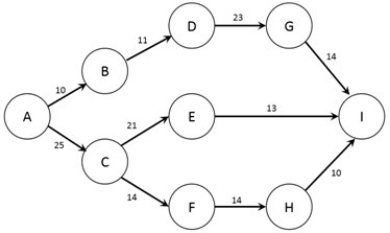Which nodes are the sink and source for this problem?

A) Node A is the sink, Node I is the source.
B) Node A is the sink, Node B is the source.
C) Node B is the sink, Node I is the source.
D) Node B is the source, Node I is the sink.
E) Node A is the source, Node I is the sink.

Question 64

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 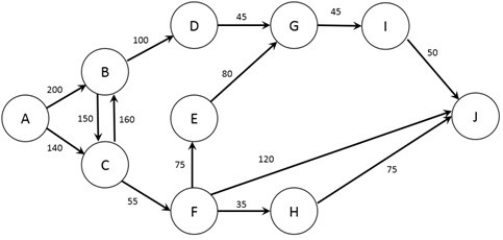Which type of network optimization problem is used to solve this problem?

A) Maximum-Cost Flow problem
B) Average-Cost Flow problem
C) Maximum Flow Problem
D) Minimum Flow Problem
E) Shortest Path Problem

Question 65

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 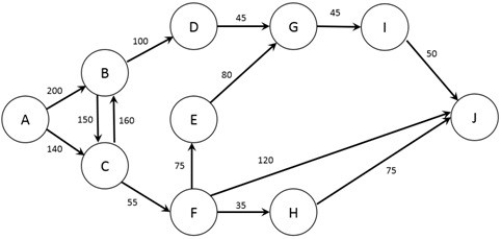Which nodes are the origin and destination for this problem?

A) Node A is the origin, Node J is the destination.
B) Node A is the origin, Node M is the destination.
C) Node B is the origin, Node I is the destination.
D) Node B is the destination, Node I is the origin.
E) Node A is the destination, Node I is the origin.

Question 66

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 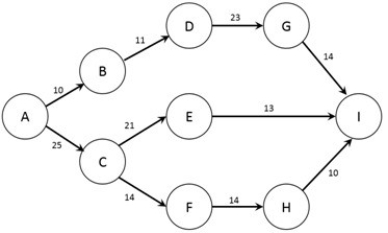What is the capacity of the connection between nodes F and H?

A) 3 TB/s
B) 4 TB/s
C) 10 TB/s
D) 14 TB/s
E) 15 TB/s

Question 67

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 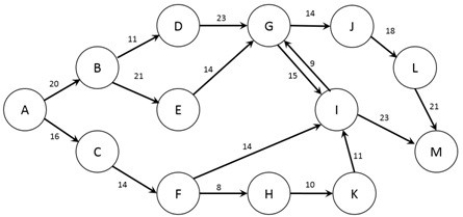Which of the following paths would be infeasible?

A) A-B-D-G-J-L-M
B) A-B-E-G-J-L-M
C) A-C-F-H-K-M
D) A-B-D-G-I-M
E) A-C-F-I-G-J-L-M

Question 68

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 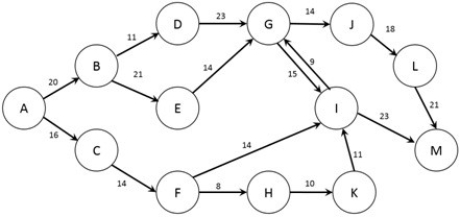Which nodes are the origin and destination for this problem?

A) Node A is the origin, Node I is the destination.
B) Node A is the origin, Node M is the destination.
C) Node B is the origin, Node I is the destination.
D) Node B is the destination, Node I is the origin.
E) Node A is the destination, Node I is the origin.

Question 69

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 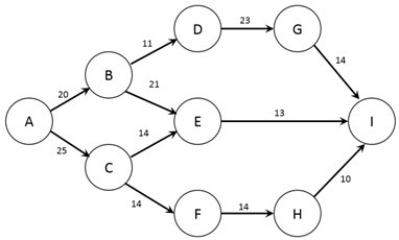How many transshipment nodes are present in this problem?

A) 6
B) 7
C) 8
D) 1
E) 2

Question 70

The figure below shows the nodes (A - I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 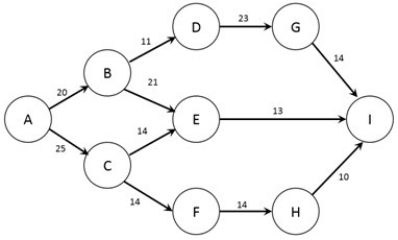Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the maximum amount of data that can be transmitted from node A to node I?

A) 13 packages/day.
B) 23 packages/day.
C) 34 packages/day.
D) 43 packages/day.
E) 53 packages/day.

Question 71

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 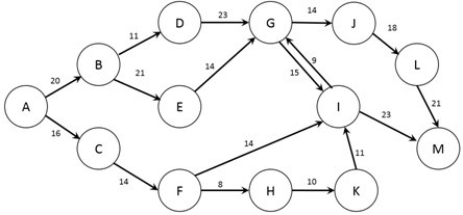Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. Which of the following nodes are not visited?

A) A
B) B
C) C
D) A and B
E) A and C

Question 72

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 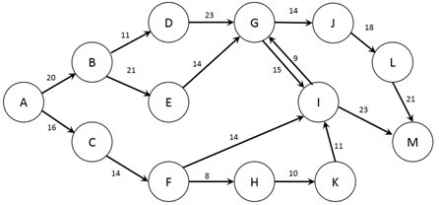Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the minimum cost for the traveler to move from node A to node M?

A) $76
B) $86
C) $96
D) $106
E) $116

Question 73

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 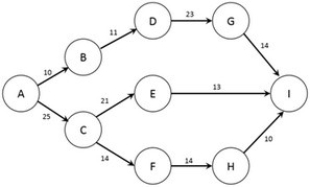Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. At maximum capacity, what will be the data flow between nodes F and H?

A) 3 TB/s
B) 4 TB/s
C) 10 TB/s
D) 14 TB/s
E) 15 TB/s

Question 74

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 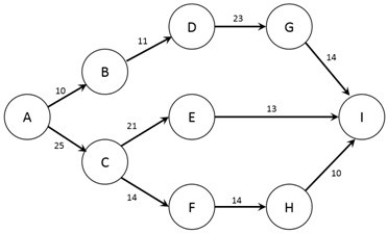Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. What is the maximum amount of data that can be transmitted from node A to node I?

A) 13 TB/s
B) 23 TB/s
C) 33 TB/s
D) 43 TB/s
E) 53 TB/s

Question 75

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 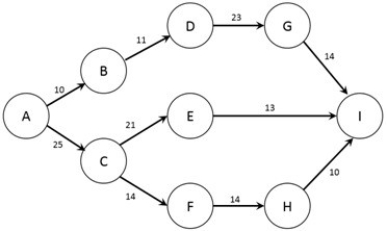Which type of network optimization problem is used to solve this problem?

A) Maximum-Cost Flow problem
B) Minimum-Cost Flow problem
C) Maximum Flow Problem
D) Minimum Flow Problem
E) Shortest Path Problem

Question 76

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 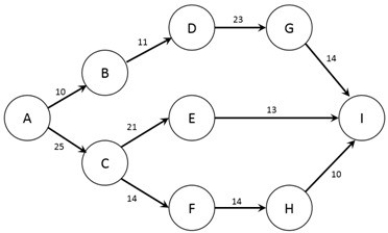How many transshipment nodes are present in this problem?

A) 6
B) 7
C) 8
D) 1
E) 2

Question 77

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 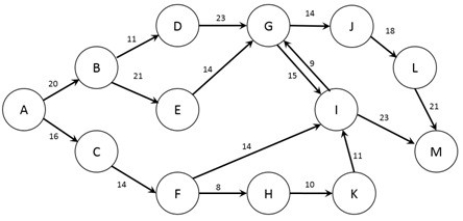Which type of network optimization problem is used to solve this problem?

A) Maximum-Cost Flow problem
B) Average-Cost Flow problem
C) Maximum Flow Problem
D) Minimum Flow Problem
E) Shortest Path Problem

Question 78

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 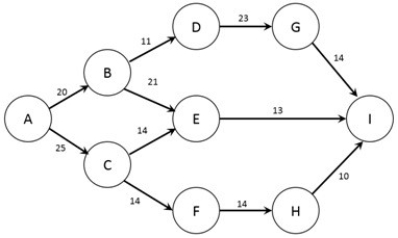Which nodes are the sink and source for this problem?

A) Node A is the sink, Node I is the source.
B) Node A is the sink, Node B is the source.
C) Node B is the sink, Node I is the source.
D) Node B is the source, Node I is the sink.
E) Node A is the source, Node I is the sink.

Question 79

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 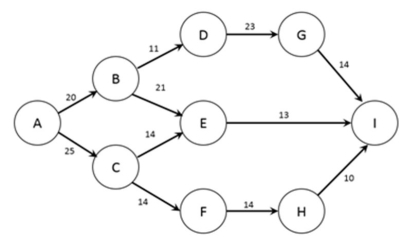Note: This question requires Solver.
Formulate the problem in Solver and find the optimal solution. At maximum capacity, what will be the flow between nodes B and E?

A) 9 packages/day
B) 11 packages/day
C) 16 packages/day
D) 21 packages/day
E) 26 packages/day

Question 80

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 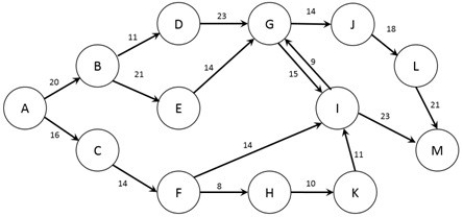What is the cost of the connection between nodes K and I?

A) 9
B) 11
C) 16
D) 21
E) 26