Exam 6: Network Optimization Problems

For a minimum cost flow problem to have a feasible solution, which of the following must be true?

Each node in a minimum cost flow problem where the net amount of flow generated is a fixed positive number is a demand node.

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 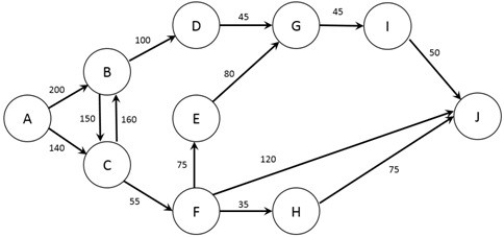What is the time to travel between nodes F and J?

The objective of a maximum flow problem is to maximize the total profit generated by sending flow through a network.

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 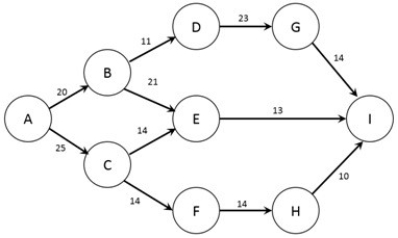Which nodes are the sink and source for this problem?

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 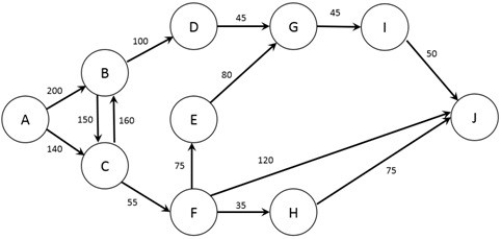Which nodes are the origin and destination for this problem?

In a shortest path problem there are no arcs permitted, only links.

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I. 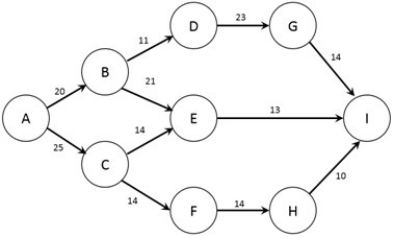What is the capacity of the connection between nodes B and E?

Any minimum cost flow problem where each arc can carry any desired amount of flow is a transshipment problem.

Any node where the net amount of flow generated is fixed at zero is a transshipment node.

A shortest path problem is required to have only a single destination.

Minimum cost flow problems are the special type of linear programming problem referred to as distribution-network problems.

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below: \text{Customer (requirement)}\\ \begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\ \text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array} How many supply nodes are present in this problem?

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 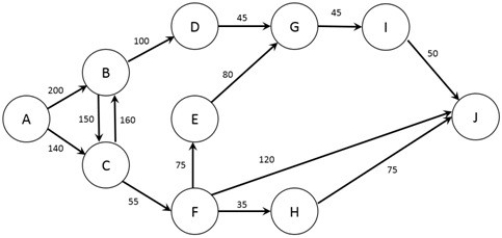Note: This question requires Solver. Formulate the problem in Solver and find the optimal solution. What is the minimum cost for the traveler to move from node A to node J?

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below: \text{Customer (requirement)}\\ \begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\ \text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array} How many demand nodes are present in this problem?

Which of the following is not an assumption of a minimum cost flow problem?

In a maximum flow problem, flow is permitted in both directions and is represented by a pair of arcs pointing in opposite directions.

A network model showing the geographical layout of the problem is the usual way to represent a shortest path problem.

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 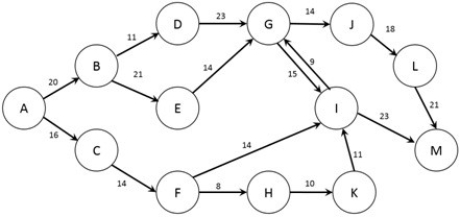Which nodes are the origin and destination for this problem?

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 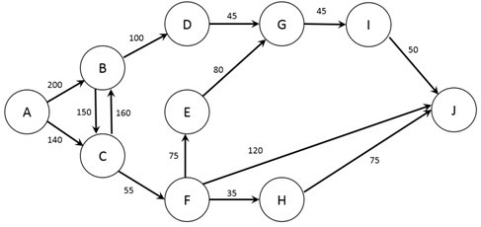Note: This question requires Solver. Formulate the problem in Solver and find the optimal solution. Which of the following nodes are not visited?