Exam 10: Introduction to Simulation Modeling
Exam 1: Introduction to Modeling30 Questions
Exam 2: Introduction to Spreadsheet Modeling30 Questions
Exam 3: Introduction to Optimization Modeling29 Questions
Exam 4: Linear Programming Models30 Questions
Exam 5: Network Models30 Questions
Exam 6: Optimization Models With Integer Variables28 Questions
Exam 7: Nonlinear Optimization Models30 Questions
Exam 8: Evolutionary Solver: an Alternative Optimization Procedure30 Questions
Exam 9: Decision Making Under Uncertainty30 Questions
Exam 10: Introduction to Simulation Modeling30 Questions
Exam 11: Simulation Models30 Questions
Exam 12: Inventory Models30 Questions
Exam 13: Queuing Models30 Questions
Exam 14: Regression and Forecasting Models30 Questions
Select questions type
Exhibit 10-1
A company is in the planning phase of constructing a new production facility.It wants to build a simulation model for the economics of the facility,and one key uncertain input is the construction cost.For each of the scenarios in the questions below,choose an "appropriate" distribution,together with its parameters,and explain your choice.
-Refer to Exhibit 10-1.Engineering also believes the construction time will be from 5 to 9 months.However,they believe that 7 months is twice as likely as either 6 months or 8 months and that either of these latter possibilities is three times as likely as either 5 months or 9 months.
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
This is another general discrete distribution,where we have to choose the probabilities so that they have the specified ratios,and add up to 1: P(5)=0.072,P(6)=0.215,P(7)=0.43,P(8)=0.215,P(9)=0.072.
The three parameters required to specify a triangular distribution are the minimum,mean and maximum.
Free
(True/False)
4.8/5  (39)
(39)
Correct Answer:
False
A correlation matrix must always be symmetric,so that the correlations above the diagonal are a mirror image of those below it.
Free
(True/False)
4.8/5  (30)
(30)
Correct Answer:
True
Exhibit 10-1
A company is in the planning phase of constructing a new production facility.It wants to build a simulation model for the economics of the facility,and one key uncertain input is the construction cost.For each of the scenarios in the questions below,choose an "appropriate" distribution,together with its parameters,and explain your choice.
-Refer to Exhibit 10-1.Management believes the facility construction time will be somewhere from 5 to 9 months.They believe the probabilities of the extremes (5 and 9 months)are both 10%,and the probabilities will vary linearly from those endpoints to a most likely value at 7 months.
(Essay)
4.9/5  (41)
(41)
If x is a random number between 0 and 1,then we can use x to simulate a variable that is uniformly distributed between 100 and 200 using the formula:
(Multiple Choice)
4.8/5  (38)
(38)
Excel's standard functions,along with the RAND function,can be used to generate random numbers from many different types of probability distributions.
(True/False)
4.9/5  (40)
(40)
One of the primary advantages of simulation models that they enable managers to answer what-if questions about changes in systems without actually changing the systems themselves.
(True/False)
4.9/5  (40)
(40)
Discrete distributions are sometimes used in place of continuous distributions:
(Multiple Choice)
4.9/5  (38)
(38)
Which of the following statements is true regarding the Triangular distribution?
(Multiple Choice)
4.7/5  (36)
(36)
A common guideline for constructing a 95% confidence interval is to place upper and lower bounds one standard error on either side of the mean.
(True/False)
4.9/5  (39)
(39)
Exhibit 10-2
A large apparel company wants to determine the profitability of one of its most popular products,a particular type of jacket.Demand is uncertain,due to economic conditions,competition,weather and other factors,and the following probability distributions have been estimated for each of the company's three regions:
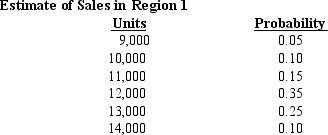

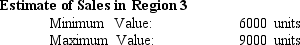 -Refer to Exhibit 10-2.Finally,suppose the apparel company receives an uncertain fraction of the total retail revenue from its retailers,modeled as a Triangular(0.70,0.75,0.80)distribution,and then must subtract production and operations costs,which are modeled as a Lognormal distribution with mean of $1,000,000 and standard deviation of $300,000.In that case,what is the expected net profit from the jacket line?
-Refer to Exhibit 10-2.Finally,suppose the apparel company receives an uncertain fraction of the total retail revenue from its retailers,modeled as a Triangular(0.70,0.75,0.80)distribution,and then must subtract production and operations costs,which are modeled as a Lognormal distribution with mean of $1,000,000 and standard deviation of $300,000.In that case,what is the expected net profit from the jacket line?
(Essay)
4.7/5  (44)
(44)
Exhibit 10-2
A large apparel company wants to determine the profitability of one of its most popular products,a particular type of jacket.Demand is uncertain,due to economic conditions,competition,weather and other factors,and the following probability distributions have been estimated for each of the company's three regions:


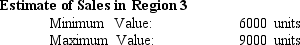 -Refer to Exhibit 10-2.Suppose the jacket sales price also varies,depending on the individual retailers and their pricing strategies.Assume that sales price is normally distributed with a mean of $65 per unit and a standard deviation of $10.How much revenue will the jacket line produce (ignore discounting)?
-Refer to Exhibit 10-2.Suppose the jacket sales price also varies,depending on the individual retailers and their pricing strategies.Assume that sales price is normally distributed with a mean of $65 per unit and a standard deviation of $10.How much revenue will the jacket line produce (ignore discounting)?
(Essay)
4.8/5  (30)
(30)
When the value of a decision variable has been optimized by running several simulations,attitude toward risk should no longer be relevant.
(True/False)
4.7/5  (37)
(37)
It is usually fairly straightforward to predict the shape of the output distribution from the shape(s)of the input distribution(s).
(True/False)
4.8/5  (39)
(39)
Exhibit 10-2
A large apparel company wants to determine the profitability of one of its most popular products,a particular type of jacket.Demand is uncertain,due to economic conditions,competition,weather and other factors,and the following probability distributions have been estimated for each of the company's three regions:


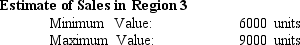 -Refer to Exhibit 10-2.Use @RISK distributions to generate the three random variables for regional sales and derive a distribution for the total sales.What is the expected total sales?
-Refer to Exhibit 10-2.Use @RISK distributions to generate the three random variables for regional sales and derive a distribution for the total sales.What is the expected total sales?
(Short Answer)
4.9/5  (23)
(23)
Exhibit 10-1
A company is in the planning phase of constructing a new production facility.It wants to build a simulation model for the economics of the facility,and one key uncertain input is the construction cost.For each of the scenarios in the questions below,choose an "appropriate" distribution,together with its parameters,and explain your choice.
-If you add n lognormally distributed random numbers,the mean of the distribution for the sum is the sum of the individual means,and the variance of the distribution of the sum is the individual variances.This result is difficult to prove mathematically,but it is easy to demonstrate with simulation.To do so,run a simulation where you add three lognormally distributed random numbers,with means of 300,700 and 100,and standard deviations of 20,50,and 30,respectively.Your single output variable should be the sum of these three numbers.Verify with @RISK that the distribution of this output has a mean of 1,000 and standard deviation 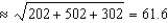 .
.
(Short Answer)
4.9/5  (33)
(33)
If a model contains uncertain outputs,it can be very misleading to build a deterministic model by using the means of the inputs to predict an output.This is called the:
(Multiple Choice)
5.0/5  (37)
(37)
Which of the following statements is true regarding the Normal distribution?
(Multiple Choice)
4.7/5  (28)
(28)
The RAND()function in excel models which of the following probability distributions?
(Multiple Choice)
4.8/5  (34)
(34)
Which of the following is not one of the important distinctions of probability distributions?
(Multiple Choice)
4.8/5  (36)
(36)
Showing 1 - 20 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)