Exam 12: The Theory of Games

Game Matrix IV The following questions refer to the game matrix below. Player A can play the strategies UP and DOWN and Player B can play the strategies LEFT and RIGHT. 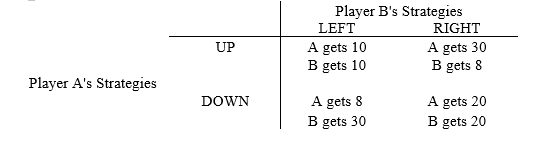-Refer to Game Matrix IV.The Nash Equilibrium for the game is

Game Matrix II The following questions refer to the game matrix below. Player A can play the strategies "High" and "Low," and Player B can play the strategies "Odd" and "Even." 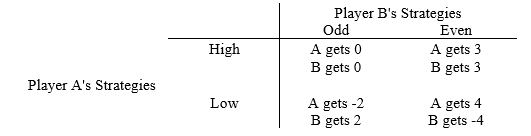-Refer to Game Matrix II.Assume this game is played sequentially.When is the Stackelberg equilibrium of this game also Pareto optimal?

The diagram used to show one player's strategies across the top and the other player's strategies along the left,with the corresponding outcomes in the appropriate boxes is a

Consider a game in which all outcomes give the players the same total payoff.Explain why every outcome in such a game will be Pareto optimal.

Game Matrix II The following questions refer to the game matrix below. Player A can play the strategies "High" and "Low," and Player B can play the strategies "Odd" and "Even." -Refer to Game Matrix II.When would the upper left-hand corner be the likely outcome of this game?

For a Nash equilibrium to exist,at least one player must have a dominant strategy.

Game Matrix V The following questions refer to the game matrix below. Each firm has a choice of saying Yes or NO. The profits each gets depend upon which it chooses. -Refer to Game Matrix V.Which of the following values of X and Y result in there being no pure strategy Nash Equilibrium?

A game's outcome is a Nash equilibrium when

Nash equilibrium is a normative concept.

In any game situation,at least one player always has a dominant strategy.

All outcomes in the Copycat Game are Nash equilibria.

When both players in a game play a dominant strategy,the outcome will be

When a game is played sequentially,the first player will have an advantage over the second player.

Fuji and Kodak produce identical film.The market demand for film is given by P = 8 - Q,where P is the price (in dollars per roll of film)and Q is the quantity (in hundreds of rolls).Each firm has the option of producing 150,200,or 300 rolls of film at a constant marginal cost of $2 per roll with no fixed costs.The firms' possible profits for various outcomes are summarized in the accompanying table.

If either player is receiving his maximum payoff,then that outcome is Pareto optimal.

Game Matrix III The following questions refer to the game matrix below. Each firm has a choice of advertising, Ads, or not advertising, No ad. The profits each gets depend upon which it chooses. -Refer to Game Matrix III.In this game,

When both players have dominant strategies,there is only one Nash equilibrium.

Consider a two-person,two-strategy game in which only pure strategies are played.Such a game must have at least one

If mixed strategies are allowed in the Copycat Game,a Nash equilibrium will result if

Consider a game in which a player has a dominant strategy.