Exam 9: Infinite Series
Exam 1: Preparation for Calculus96 Questions
Exam 2: Limits and Their Properties119 Questions
Exam 3: Differentiation208 Questions
Exam 4: Applications of Differentiation147 Questions
Exam 5: Integration165 Questions
Exam 6: Differential Equations88 Questions
Exam 7: Applications of Integration90 Questions
Exam 8: Integration Techniques, L'Hôpital's Rule, and Improper Integrals142 Questions
Exam 9: Infinite Series199 Questions
Exam 10: Parametric Equations, Polar Coordinates, and Vectors173 Questions
Exam 11: Mechanical Ventilation and Sedation: Assessment, Medications, and Complications225 Questions
Select questions type
Use the Ratio Test to determine the convergence or divergence of the series. 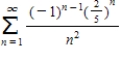
(Multiple Choice)
4.9/5  (36)
(36)
Consider the function given by 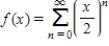 .Find the interval of convergence for
.Find the interval of convergence for  .
.
(Multiple Choice)
4.7/5  (41)
(41)
Find the fourth degree Taylor polynomial centered at 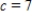 for the function.
for the function. 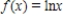
(Multiple Choice)
4.9/5  (33)
(33)
Let 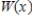 be the Taylor expansion for
be the Taylor expansion for 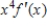 about
about 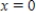 .Find the general term for
.Find the general term for 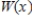 and find
and find 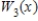 .
.
(Essay)
4.9/5  (38)
(38)
Use the definition to find the Taylor series centered at 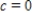 for the function
for the function 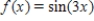 .
.
(Multiple Choice)
4.8/5  (43)
(43)
Find the interval of convergence of the power series.(Be sure to include a check for convergence at the endpoints of the interval. ) 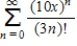
(Multiple Choice)
4.8/5  (26)
(26)
Identify the graph of the first 10 terms of the sequence of partial sum of the series 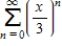 for
for 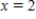 .
.
(Multiple Choice)
4.8/5  (28)
(28)
Use the Ratio Test to determine the convergence or divergence of the series. 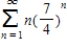
(Multiple Choice)
4.8/5  (33)
(33)
Find a geometric power series for the function 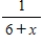 centered at 0.
centered at 0.
(Multiple Choice)
4.8/5  (38)
(38)
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of f at  .What is P1 called?
.What is P1 called? 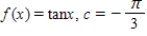
(Multiple Choice)
4.8/5  (32)
(32)
Suppose the winner of a $15,000,000 sweepstakes will be paid $500,000 per year for 30 years,starting a year from now.The money earns 5% interest per year.The present value of the winnings is 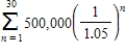 Compute the present value using the formula for the nth partial sum of a geometric series.Round your answer to two decimal places.
Compute the present value using the formula for the nth partial sum of a geometric series.Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (39)
(39)
Use the definition to find the Taylor series (centered at c)for the function. 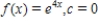
(Multiple Choice)
4.7/5  (36)
(36)
Let 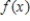 be a function that is differentiable for all
be a function that is differentiable for all  .The Taylor expansion for
.The Taylor expansion for 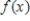 about
about 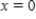 is given by
is given by 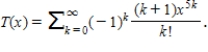 The first four nonzero terms of
The first four nonzero terms of 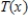 are given by
are given by 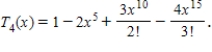 -Show that
-Show that 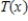 converges for all
converges for all  .
.
(Essay)
4.8/5  (40)
(40)
The sixth degree term of the Taylor series expansion for 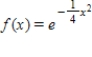 about
about 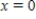 has coefficient
has coefficient
(Multiple Choice)
4.9/5  (41)
(41)
Use Theorem 9.11 to determine the convergence or divergence of the series. 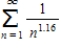
(Multiple Choice)
4.8/5  (40)
(40)
Write the first five terms of the sequence of partial sums. 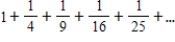
(Multiple Choice)
4.8/5  (31)
(31)
Use the Limit Comparison Test to determine the convergence or divergence of the series 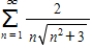 .
.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 141 - 160 of 199
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)